Purpose/Introduction

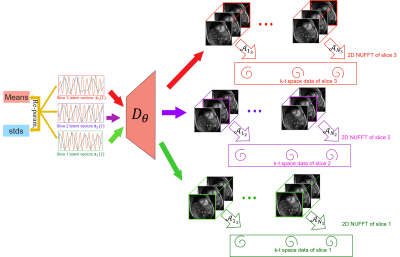
Breath-held multi-slice cine MRI is an integral part of clinical cardiac exams. While several conventional [1] and deep-learning based [2] acceleration schemes had been introduced to reduce the breath-hold duration, these approaches are still infeasible for several subject groups that cannot hold their breath. Free-breathing imaging schemes, including navigated or self-gating [3, 4] methods and kernel manifold approaches [5,6] had been introduced to recover the data from several cardiac and respiratory cycles. All of the above approaches independently reconstruct the data from different slices; they often require sophisticated post-processing methods to align the data from different slices. Another challenge is the inability to exploit the extensive inter-slice redundancies, which can be used to reduce the scan duration.

The main focus of this abstract is to introduce a manifold learning framework for the alignment and joint reconstruction of data from independent 2D multi-slice acquisitions. The 3D volumes corresponding to different time points are assumed to live on a smooth low-dimensional manifold. In particular, we consider a CNN that generates the 3D image volume, when driven by a low-dimensional latent vector. We propose to learn the CNN parameters and the latent vector time series corresponding to each slice jointly from the k-t space data from all the slices. We expect the latent vectors of each slice to capture the cardiac and respiratory motion patterns during the acquisition of that specific slice. The same 3D generator is used for all slices (see Fig. 1 for an illustration). Once learned, the generator will be excited with the latent vectors of any slice, when we expect the generator to recover aligned image time series.

Methods

To facilitate the alignment of the images from multiple slices which differ in cardiac or respiratory patterns, we formulate the recovery as a variational scheme. The variational approach allows us to impose priors on the latent vectors, which will encourage the latent vectors of different slices to have the same distribution. This approach can be viewed as the generalization of the variational auto-encoder (VAE) to the under-sampled setting.

We model the acquisition of the data as
$$\mathbf b(t_z) = \mathcal{A}_{t_z}\Big(\mathbf{x}(\mathbf r,t_z)\Big) + \mathbf n_{t_z},$$
where $$$\mathbf b(t_z) $$$ is the k-t space data of the $$$z^{\rm th}$$$ slice at the $$$t^{\rm th}$$$ time frame and $$$\mathcal{A}_{t_z}$$$ are the time dependent measurement operators, which evaluates the multi-channel single slice Fourier measurements of the 3D volume $$$\mathbf x(\mathbf r,t_z)$$$. We model the volumes in the time series as
$$\mathbf x_i = \mathcal D_{\theta}(\mathbf c_i),$$
where $$$\mathbf c_i$$$ is latent variable corresponding to $$$\mathbf x_i$$$ and $$$\mathcal D_{\theta}$$$ is a CNN-based generator with parameters $$$\theta$$$, which are shared for all image volumes. We formulate the joint learning of $$$\theta$$$ and $$$\mathbf c_i = \boldsymbol \mu_i + \boldsymbol \Sigma_i ~\boldsymbol\epsilon, \,\,\,\boldsymbol \epsilon = \mathcal{N}(\mathbf{0},\mathbf{I})$$$ as the minimization of
$$\mathcal{L}_{MS}(\theta,\boldsymbol{\mu}(t_z),\boldsymbol \Sigma(t_z)) = \mathcal C_{MS}(\theta,\boldsymbol{\mu}(t_z),\boldsymbol \Sigma(t_z)) + \lambda_1||\theta||_1^2 + \lambda_2\sum_z||\nabla_{t_z}\boldsymbol{\mu}(t_z)||^2,$$
where
$$\mathcal C_{MS} = \displaystyle\sum_{z=1}^{N_{\rm slice}}\sum_{t=1}^{N_{\rm data}}\|\mathcal{A}_{t_z}\left[\mathcal D_{\theta}(\mathbf c(t_z))\right] - \mathbf b_{t_z}\|^2+\sigma^2~ L(q(t_z)).$$

The first term is the data consistency term, while the second term encourages the latent vectors to follow a Gaussian distribution, specified by $$$q$$$. The third term is a regularization penalty on the CNN parameters, while the last term penalizes the temporal smoothness of the latent vectors.

Results

The proposed scheme is illustrated on spiral multi-slice datasets, acquired with 25 secs/slice with TR=8.4 ms from a volunteer and a COPD subject. The datasets have 8 and 6 slices, respectively. To demonstrate the benefit of the proposed generative SToRM (g-SToRM) [7] scheme, we only use 6 seconds of data/slice for image recovery. Fig. 2 shows the image quality comparisons with state-of-the-arts method, including slice-by-slice analysis SToRM (a-SToRM) [6] that uses kernel low-rank regularization. The a-SToRM reconstructions from 25 s/slice is used as reference. Fig. 3 and Fig. 4 show the results on the joint alignment and recovery of two datasets. Post-recovery, we slice the 3D volumes to display the long axis view of the heart, to demonstrate the alignment of the slices.

Conclusion

The proposed scheme enables the alignment of multiple slices acquired serially with a spiral multi-slice acquisition scheme, followed by the joint recovery of the 3D volumes. The joint reconstruction capitalizes on the inter-slice similarities, which enables the reduction in scan time to 6 secs/slice from 25 secs/slice needed for slice-by-slice reconstruction schemes. Post-recovery, the 3D volumes can be displayed with arbitrary 2D views.

Acknowledgements

This work is supported by NIH under Grants R01EB019961 and R01AG067078-01A1. This work was conducted on an MRI instrument funded by 1S10OD025025-01.