Motivation

In diffusion weighted imaging, “long” diffusion gradient pulses are usually employed that satisfy $D\delta\gg L^2$ , where $D$ is the free diffusion coefficient, $\delta$ the duration of the gradient pulses, and $L$ the characteristic length-scale of the diffusion restrictions (i.e. the cell diameter).
Because of technical limitations, it is often not possible to achieve short diffusion gradient pulses (i.e. $D\delta\ll L^2$ ). The diffusion weighting is proportional to $G^2\delta^2$ , with the gradient amplitude $G$ , and therefore longer pulses are often needed to achieve high enough diffusion weighting. However, if such short pulses are achievable, the MR diffusion experiment has an interesting property [2]: The diffusive motion of the particles during the pulse can be neglected and hence the volume averaged diffusion propagator can be measured [1,3,4].
In the limit of long diffusion time $\Delta$ between the gradient pulses, the diffusion propagator is often highly correlated with the microscopic structure of the underlying tissue. Additionally the diffusion propagator and the measured signal curve have a Fourier relation. In the case of a well-defined length scale of the underlying diffusion restrictions, the signal shows characteristic oscillations or “peaks”, which in return allow predictions about the tissue structure.
To the knowledge of the authors, in the case of long diffusion gradient pulses such characteristic oscillations have not yet been shown in simulation or experiment. In the present work, it is shown that such oscillations or “signal peaks” can occur for long diffusion gradient pulses in theory. Additionally, simulations for the exemplary case of a simple one-dimensional model are presented.[5]

Theory

According to Mitra and Halperin, the diffusion-weighted signal can be expressed as
$$S({\bf q}) = \langle \text{exp} \left( -i {\bf q} \cdot \left({\bf x}_\text{cm,2}-{\bf x}_\text{cm,1}\right)\right)\rangle, \tag{1}$$
where $|{\bf q}|=\gamma G\delta$ and bipolar gradient pulses of amplitude $G$ and duration $\delta$ are assumed [2]. ${\bf x}_\text{cm,1}$ and ${\bf x}_\text{cm,2}$ describe the centers of mass of the particle trajectories during the gradient pulses. The angle brackets denote the average over all particles (cf. Fig.1).
In the limit of $\delta \to 0$, one obtains ${\bf x}_\text{cm,1} \to {\bf x}_\text{1}$ and ${\bf x}_\text{cm,2} \to {\bf x}_\text{2}$, where ${\bf x}_\text{1}$ and ${\bf x}_\text{2}$ are the start and end points of the particle trajectories. For $\Delta \gg L^2 / D$ one gets
$$S({\bf q}) = | \tilde{\chi} ({\bf q})|^2 \tag{2}$$
for enclosed pores, where $\tilde{\chi} ({\bf q})$ is the Fourier transform of the pore space function $\chi({\bf r })$, which is 1 inside the pore and 0 elsewhere [1].
$|\tilde{\chi} ({\bf q})|^2$ shows oscillations in q-space, the Fourier domain of the real space, which scale with the inverse length scale $L^{-1}$.
Taking into account the finite permeability of membranes, i.e. particles are allowed to diffuse from one pore to another, one can rewrite eq.1 in the limits $\delta>L^2/D$ and $\delta\approx\tau\ll\Delta$, where $\tau$ is the average lifetime of a particle inside one pore:
$$S({\bf q}) = \sum_{n,m} P_{n,m}(\Delta)\text{exp} \left( i {\bf q} \cdot \left({\bf x}_{\text{cm,pore,}n}-{\bf x}_{\text{cm,pore,}m}\right)\right)$$
Where ${\bf x}_{\text{cm,Pore,}m}$ is the center of mass of pore $m$ and $P_{n,m}(\Delta)$ denotes the probability of a particle diffusing from pore $n$ to pore $m$. As all pores shall be equivalent and only translations are important with respect to the diffusion weighted signal one can set $n=0$ and hence ${\bf x}_{\text{cm,pore,}n}=0$ , which yields:
$$S_{n=0}({\bf q})\approx\sum_{m}P_{m}(\Delta)\text{exp} \left(-i{\bf q}\cdot{\bf x}_{\text{cm,pore,}m}\right) \tag{3}$$
Therefore, which is the most important statement of the present work, one can measure the Fourier transform of the pore distribution function.

Methods

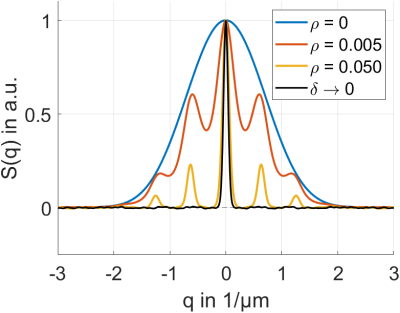
The diffusion weighted signal curve in the case of long diffusion gradient pulses is investigated by random walk simulations in the model geometry of infinitely long, parallel, permeable plates (cf. fig.1). In this case $S_{n=0}({\bf q})$ is a Dirac-Delta comb, which is modulated by $P_{m}(\Delta)$. The distance between the Dirac-Delta functions in the comb is $2\pi L^{-1}$. The following simulation parameters have been employed: plate distance $L=10$ µm, $D=2$ µm²/ms, $\delta=0.1$ and $50$ ms, $\Delta=300$ ms, membrane permeability $\rho=0, 0.005$ and $0.05$ µm/ms, number of steps $=1,000$, step size $=0.04$ µm, number of particles $=100,000$.

Results

For long diffusion gradient pulses, signal peaks appear at multiples of $q=2\pi L^{-1}$. The Dirac-Delta comb becomes visible (cf. fig.2). Line broadening (due to the limit $x_\text{cm}\to{x}_\text{cm,pore}$ not being perfect) and an envelope (due to particles not being able to explore the whole lattice during $\Delta$) are apparent.

Discussion

Signal peaks for short gradient pulses have been reported repeatedly [1,2,3,4]. However, for long gradient pulses, only Mitra and Halperin mention the possibility of signal peaks to our knowledge, which they call “Bragg peaks”[2]. In the present work, it is shown explicitly that signal peaks can occur for long gradient pulses as well.
For both, short and long gradient pulses these peaks only appear if the underlying structure of diffusion restrictions is of a periodic nature. Eq.3 however is true also in the case of non-periodic structures.

Conclusion

The pores can be approximated as closed pores, due to the limits $\delta>L^2/D$ and $\delta\approx\tau\ll\Delta$, for the duration of a single gradient pulse. Therefore, the fraction of particles that stay in one pore during the gradient pulses result in a signal that is described by the Fourier transform of the pore distribution function.

Acknowledgements

No acknowledgement found.