0982
Violation of axial-symmetric assumption in DKI and consequences for biophysical parameter estimates across white matter1Institute of Systems Neurosciences, University Medical Center Hamburg-Eppendorf, Hamburg, Germany, 2Weierstrass Institute for Applied Analysis and Stochastics, Berlin, Germany, 3Department of Neurophysics, Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany
Synopsis
The recently introduced axial-symmetric DKI framework is less noise sensitive but unable to capture more complex fiber configurations causing an AxDKI inherent bias in those voxels. We found that the parallel and perpendicular kurtosis are most often affected by this inherent bias and that it translates to the AxDKI based biophysical parameters. Bias-free estimation of the biophysical parameters with the AxDKI framework, therefore, is difficult if not impossible at this point. However, the parallel and perpendicular diffusivity and the mean kurtosis were largely bias-free, encouraging use of the AxDKI framework in studies where these parameters are focused on.
Introduction:
The axial-symmetric diffusion kurtosis imaging (AxDKI) signal framework1 has recently attracted attention because it is less susceptible to noise and its parameters are directly linked to the biophysical parameters intra- and extra axonal diffusivity, fiber dispersion and axonal water fraction2,3. While complex fibre configurations as they appear in human brains can representatively be mapped with standard DKI4,5, AxDKI is based on the assumption of axial-symmetrically distributed axons around an axis of symmetry. This assumption can be violated in complex, non-axial symmetric fiber configurations causing a so-called “tissue-specific AxDKI inherent bias”. Here we investigate this bias and its translation to the biophysical parameters on noise-free white matter (WM) simulations with a specific focus on five well-known fiber tracts, Figure 1. We compare AxDKI and standard DKI parameter estimators on a voxel-wise basis, implicitly assuming that any deviation from the standard DKI estimators (ground truth) is due to the AxDKI inherent bias caused by complex fiber configurations.Methods:
MRI parameters for simulation: Multi-shell diffusion weighted imaging (DWI) data with 151 directions and b-values of 0, 500, 1250 and 2500 $$$\frac{s}{mm^2} $$$ were acquired on a healthy volunteer6 at 3T with: FOV of 240x230x154mm3 at 1.6mm isotropic resolution and $$$\frac{TE}{TR} = \frac{73ms}{5300ms}$$$. These DWI data were fitted with standard DKI to obtain the 22 standard DKI parameters used for the simulation.Simulations: Noise-free DWI data of the WM of the in-vivo dataset were simulated based on the standard DKI signal framework5 using the estimated DKI parameters.
AxDKI inherent bias investigation: All five biophysically-relevant diffusion kurtosis parameters $$$ \theta={D_\parallel,D_\bot,\ W_\parallel,\ W_\bot,\ \bar{W}} $$$ were estimated with AxDKI and standard DKI and compared using the voxel-wise bias $$$100\cdot\frac{\left|\theta_i^{DKI}(r_k)-\theta_i^{AxDKI}(r_k)\right|}{\theta_i^{DKI}(r_k)} $$$ , where $$$\theta_i^{DKI},\theta_i^{AxDKI}\in\theta $$$ for $$$i=1,\ldots,5 $$$ and $$$r_k $$$ is the $$$k$$$-th voxel position. If the voxel-wise bias was greater 5% the voxel was classified as “inherently biased”. We analyzed the whole WM and five fiber tracts identified with the JHU-ICBM-DTI-81 WM atlas7, see Figure 1. For the fiber tract analysis, the JHU-ICBM-DTI-81 WM atlas was non-linearly registered to the individual subject space of the recorded DWI data using the spatial normalization tool in SPM12.
Additionally, the five biophysical parameters $$$\beta={f,\kappa,\ D_{e,\bot},\ D_{e,\parallel},D_a\ }$$$ were estimated based on $$$\theta^{DKI}$$$ (or $$$\theta^{AxDKI}$$$) solving the set of equations presented in3,8, and the relative difference between $$$\beta^{AxDKI}$$$ and $$$\beta^{DKI}$$$ were calculated as defined above. Note that we only report the results for the positive branch of solutions in8, since we found that the negative branch produced biologically unrealistic values. All processing and model fitting is MATLAB-based and freely available online within the ACID Toolbox (http://www.diffusiontools.com/).
Results:
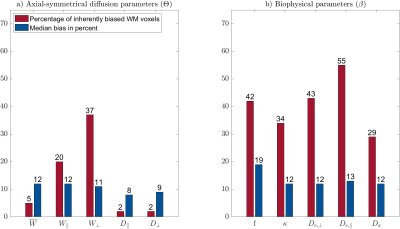
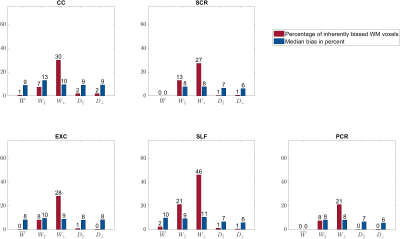
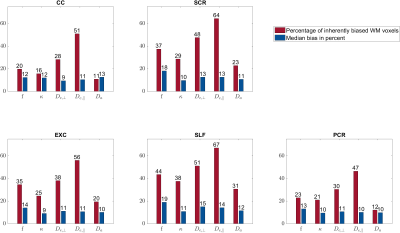
$$$\mathbf{\theta}$$$ parameters: The percentage of biased WM voxels was smallest in the diffusion parameters $$$D_\bot, D_\parallel$$$ (each 2%) and the kurtosis parameter $$$\bar{W}$$$ (5%), see Figures 2 and 3a. $$$W_\parallel$$$ (20%) and $$$W_\bot $$$(37%) contained the largest amount of inherently biased voxels. Almost the same pattern showed up in the selected fibre tracts, Figure 4, except for $$$\bar{W}$$$ which was less frequently biased in the selected fibre tracts than in the entire WM. Moreover, the amount of inherently biased voxels was larger in the superior longitudinal fasciculus than in the whole WM, whereas it was smaller for the other fibre tracts. The median bias of the inherently biased voxels was between 8% and 13% without a distinctive pattern among the parameters.Biophysical parameters: The biophysical parameters were inherently biased in 29% ($$$D_a$$$) to 55% ($$$D_{e,\parallel}$$$) of all WM voxels, see Figure 3b. $$$D_{e,\parallel}, D_{e,\bot}$$$ and $$$f$$$ were most often inherently biased (including the five fiber tracts) while $$$D_a$$$ and $$$\kappa$$$ were always least biased. Again, the amount of inherently biased voxels was larger in the superior longitudinal fasciculus than in the whole WM, whereas no consistent trend was observable for the other fibre tracts, see Figure 5. The median bias of the inherently biased voxels ranged from 9% to 19% without a distinctive pattern among the parameters.
Discussion and Conclusion
Our results showed that the AxDKI inherent bias in WM cannot be neglected for the DKI parameters $$$W_\bot$$$ and $$$W_\parallel$$$, whereas it is negligible for the other parameters ($$$D_\bot, D_\parallel$$$ and $$$\bar{W}$$$). For the biased parameters, we found that it varied between fiber tracts, potentially resembling the varying complexity of fiber configurations between fiber tracts. The biophysical parameters were generally more often affected by the AxDKI inherent bias (up to 55% of all WM voxels and 67% in fiber tracts), demonstrating a broader translation of the inherent bias in the $$$\theta^{AxDKI}$$$ parameters (especially $$$W_\parallel$$$ and $$$W_\bot$$$) into the biophysical parameters. However, the median bias of the biophysical parameters only ranged from 9% to 19% which might be an acceptable range depending on the performed study. In summary, our findings encourage studies that focus on the commonly used DKI parameters ($$$D_\bot, D_\parallel$$$ and $$$\bar{W}$$$) to use the AxDKI framework and profit from its higher noise robustness, whereas for the estimation of the biophysical parameters the AxDKI framework should only be used if elevated biases are acceptable. All AxDKI, DKI and biophysical parameter estimation tools are freely available online as part of the ACID toolbox.Acknowledgements
This work was supported by the German Research Foundation (DFG Priority Program 2041 "Computational Connectomics”, [MO 2397/5-1,2], by the Emmy Noether Stipend: MO 2397/4-1) and by the BMBF (01EW1711A and B) in the framework of ERA-NET NEURON.References
1. Hansen, B., Shemesh, N. & Jespersen, S. N. Fast imaging of mean, axial and radial diffusion kurtosis. NeuroImage 142, 381–393 (2016).
2. Fieremans, E., Jensen, J. H. & Helpern, J. A. White matter characterization with diffusional kurtosis imaging. NeuroImage 58, 177–188 (2011).
3. Jespersen, S. N., Olesen, J. L., Hansen, B. & Shemesh, N. Diffusion time dependence of microstructural parameters in fixed spinal cord. NeuroImage 182, 329–342 (2018).
4. Lazar, M., Jensen, J. H., Xuan, L. & Helpern, J. A. Estimation of the orientation distribution function from diffusional kurtosis imaging. Magn. Reson. Med. 60, 774–781 (2008).
5. Jensen, J. H., Helpern, J. A., Ramani, A., Lu, H. & Kaczynski, K. Diffusional kurtosis imaging: the quantification of non-Gaussian water diffusion by means of magnetic resonance imaging. Magn. Reson. Med. 53, 1432–1440 (2005).
6. Mohammadi, S. & Callaghan, M. F. Towards in vivo g-ratio mapping using MRI: Unifying myelin and diffusion imaging. J. Neurosci. Methods 108990 (2020) doi:10.1016/j.jneumeth.2020.108990.
7. Hua, K. et al. Tract Probability Maps in Stereotaxic Spaces: Analyses of White Matter Anatomy and Tract-Specific Quantification. NeuroImage 39, 336–347 (2008).
8. Novikov, D. S., Veraart, J., Jelescu, I. O. & Fieremans, E. Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI. NeuroImage 174, 518–538 (2018).
Figures
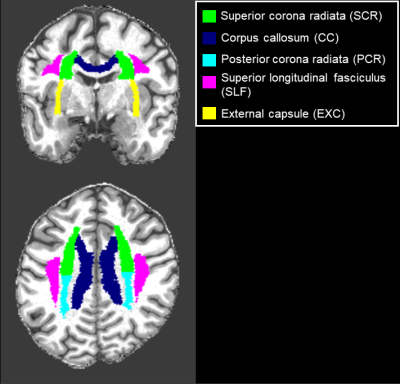
Figure 1: Analyzed WM fiber tracts, identified with the JHU-ICBM-DTI-81 WM atlas.

Figure 2: AxDKI inherent bias.
a) Top row: $$$\theta$$$ parameters computed from the 22 standard DKI parameters in a simulated WM slice. Second row: white voxels indicating inherently biased AxDKI voxels larger 5%. b) Third row: Biophysical parameters (branch “+”) computed from standard DKI. Fourth row: white voxels indicating inherently biased biophysical parameter voxels larger 5%. For numerical reasons, the units of the DKI diffusion parameters are in $$$[\frac{mm^2}{s}]$$$ and the units of the diffusion parameters of $$$\beta^{DKI}$$$ are in $$$[\frac{µm^2}{ms}]$$$.