0981
How to understand diffusion MRI changes in the white matter of Multiple Sclerosis patients?1Radiology, NYU School of Medicine, New York, NY, United States
Synopsis
Conventional diffusion MRI (dMRI) techniques, such as DTI and DKI, are sensitive to pathology but lack specificity. In brain white matter, the “Standard Model” framework of dMRI may provide specificity to microstructural changes. Generally, clinical dMRI is noisy and limited, making SM estimation challenging. Thus, different constraints and techniques have been introduced to robustly extract SM parametric maps. Here, we employ a large clinical dataset of Multiple Sclerosis patient data (N = 134) and noise propagation experiments to study the sensitivity and specificity of these techniques.
Introduction
Diffusion MRI (dMRI) and derived metrics from DTI1 and DKI2 are sensitive to pathology. To achieve microstructural specificity, the Standard Model3 (SM) framework has been proposed as an overarching dMRI model for white matter (WM) unifying many previously proposed WM models4-16. The SM signal, measured along direction $$$\hat{g}$$$, is a convolution between the fiber orientation distribution function (ODF) $$$\mathcal{P}(\hat{n})$$$ and the fiber response signal $$$\mathcal{K}(b,\hat{g}\cdot\hat{n})$$$ $$S_{\hat{g}}(b)=\int_{|\hat{n}|=1}d\hat{n}\,\mathcal{P}(\hat{n})\,\mathcal{K}(b,\hat{g}\cdot\hat{n})$$ where $$\mathcal{K}(b,\xi)=S_0\,[fe^{-bD_{a}\xi^2}+(1-f)e^{-bD_{e}^{\parallel}\xi^2-bD_e^\bot(1-\xi^2)}]$$ with $$$\xi=\hat{g}\cdot\hat{n}$$$. Here $$$[f,D_{a},D_{e}^{\parallel},D_{e}^{\bot},p_2]$$$ are intra-axonal space (IAS) fraction, IAS axial diffusivity, extra-axonal space (EAS) axial diffusivity, EAS radial diffusivity and $$$l=2$$$ rotational invariant of ODF, respectively.Due to the multi-compartmental nature of the SM, the estimation of SM parameters in clinical data is degenerate11. To resolve the degeneracy, WMTI13 and WMTI-Watson14 (denoted as Watson+ for $$$D_{a}>D_{e}^{\parallel}$$$ and Watson- for $$$D_{a}<D_{e}^{\parallel}$$$) employ relatively robust DKI metrics to derive SM parameters, while NODDI8 and SMT15 assume same axial diffusivity in IAS and EAS and the tortuosity approximation $$$D_e^{\bot}=D_e^{\parallel}\cdot(1-f)$$$. Moreover, ML-RotInv16 was employed to map $$$l=0,\,2$$$ rotational invariants to SM parameters using a data-driven approach.
Here we compare these estimation methods by assessing WM degeneration in a clinical cohort of patients with multiple sclerosis (MS), and interpret the findings using noise propagation.
Methods
In-vivo MRI:In a retrospective IRB-approved study, 134 MS patients (age 47.80 ± 9.60 years old, 91 females) and 124 matching controls (age 48.41 ± 9.95 years old, 84 females) were selected. These subjects underwent clinically indicated MRI using at 3T (Siemens Magnetom Prisma or Skyra). MS subjects received a clinical MS diagnosis using the McDonald criteria17, and control subjects were recruited from headache patients with normal brain MRI and no neurological disorders.
The dMRI protocol included a monopolar EPI sequence as follows: 4 b = 0, b = 250 s/mm2 along 4 directions, b = 1000 s/mm2 along 20 directions and b = 2000 s/mm2 along 60 directions, with imaging parameters: 50 slices, 130 × 130 matrix, voxel size = 1.7 × 1.7 × 3 mm, TE = 70 ms on Prisma or TE = 95 ms on Skyra, TR = 3500 ms, GRAPPA acceleration 2, and multiband 2.
The dMRI data was processed by DESIGNER18 for denoising19, Gibbs artifact correction20, motion and eddy correction21. SM parameters were obtained using all SM parameter estimation methods mentioned above. The genu corpus callosum (GCC) was automatically segmented by nonlinear mapping on the JHU WM label atlas22. Median values were extracted for SM and DKI metrics, and used to conduct one-way ANCOVA between control and MS groups for each parameter of interest, with group membership acting as the independent variable and controlling for patient age.
Numerical noise propagation:
Numerical noise propagation was done using synthetic dMRI signals generated with random combinations of SM parameters based on the same protocol as above. Gaussian noise at signal-to-noise ratio = 40 was added and then SM estimation methods were applied to the noisy synthetic data to predict SM parameters.
The sensitivity-specificity matrix ($$$S_{ij} = \frac{\partial \hat{\theta}_{j}}{\partial \theta_{i}}$$$) is computed through linear regression of each estimated SM parameter $$$\hat{\theta_{j}}$$$ with respect to the ground truth $$$\theta_{i}$$$ of all five SM parameters, reflecting how changes in ground truth are picked up in the estimation.
Results and Discussion
Fig. 1 shows that DKI metrics are sensitive to MS pathology, consistent with previous studies23, 24, but the underlying pathological processes remain unclear.Table 1 reveals many SM parameter changes between control and MS, but these changes are not consistent across different SM estimation methods. Clearly, the model assumptions and fitting constraints of each estimation method impact these results. To help interpret these, we performed noise propagation for all SM estimation methods.
Fig. 2 displays the sensitivity-specificity matrix for all SM estimation methods, whereby diagonal elements measure sensitivity and off-diagonal elements show specificity. The sensitivity-specificity matrix reveals how spurious findings may arise: for axial compartmental diffusivities, Watson+ has a strong negative correlation with $$$f$$$, while Watson- and WMTI have strong positive correlations with $$$p_2$$$, which makes them unreliable in estimating axial compartmental diffusivities. Furthermore, ML-RotInv has the highest sensitivity to $$$p_2$$$ demonstrated both by the sensitivity-specificity matrix and the detection of a significant change (p < 0.001) in $$$p_2$$$ between controls and MS.
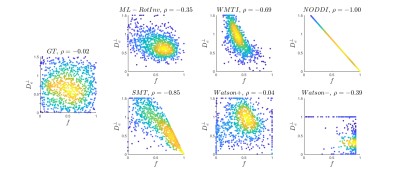
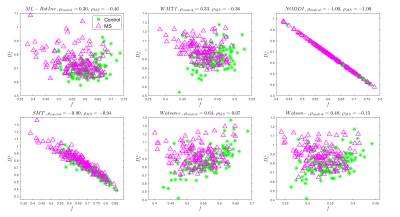
Overall, ML-RotInv seems the most robust and specific SM estimation method, and detects an increase in $$$D_e^{\bot}$$$ and decrease in $$$f$$$ (Table 1), which may reflect demyelination and axonal loss25, 26, warranting further investigation. Fig. 3,4 show scatter plots of $$$D_{e}^{\bot}$$$ versus $$$f$$$ for noise propagation and clinical data, respectively. While the negative correlation ($$$\rho=-0.46$$$) between $$$f$$$ and $$$D_e^{\bot}$$$ by ML-RotInv in MS (Fig. 4) could be due to estimation bias (Fig. 3), the positive correlation ($$$\rho=0.36$$$) in controls seems genuine. This observation is consistent among all estimation methods, except for SMT and NODDI which have a tortuosity constraint. This is contrary to what tortuosity models8, 27 assume and could potentially be understood by accounting for myelin.
Conclusions
SM estimation methods introduce spurious changes in MS pathology when applied to clinical dMRI. The sensitivity-specificity matrix reveals important insight into the specificity of each estimation method. These results also warn against employing simple constraints in microstructure imaging and argue for more realistic biophysical models.Acknowledgements
This work was performed under the rubric of the Center for Advanced Imaging Innovation and Research (CAI2R, https://www.cai2r.net), a NIBIB Biomedical Technology Resource Center (NIH P41-EB017183). Thiswork has been supported by NIH under NINDS award R01 NS088040 and NIBIB awards R01 EB027075.References
1. Basser, Peter J., James Mattiello, and Denis LeBihan. "MR diffusion tensor spectroscopy and imaging." Biophysical journal 66.1 (1994): 259-267.
2. Jensen, Jens H., et al. "Diffusional kurtosis imaging: the quantification of non‐gaussian water diffusion by means of magnetic resonance imaging." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 53.6 (2005): 1432-1440.
3. Novikov, Dmitry S., et al. "Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI." NeuroImage 174 (2018): 518-538.
4. Jespersen, Sune N., et al. "Neurite density from magnetic resonance diffusion measurements at ultrahigh field: comparison with light microscopy and electron microscopy." Neuroimage 49.1 (2010): 205-216.
5. Jespersen, Sune N., et al. "Modeling dendrite density from magnetic resonance diffusion measurements." Neuroimage 34.4 (2007): 1473-1486.
6. Assaf, Yaniv, et al. "New modeling and experimental framework to characterize hindered and restricted water diffusion in brain white matter." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 52.5 (2004): 965-978.
7. Fieremans, Els, et al. "Monte Carlo study of a two‐compartment exchange model of diffusion." NMR in Biomedicine 23.7 (2010): 711-724.
8. Zhang, Hui, et al. "NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain." Neuroimage 61.4 (2012): 1000-1016.
9. Sotiropoulos, Stamatios N., Timothy EJ Behrens, and Saad Jbabdi. "Ball and rackets: inferring fiber fanning from diffusion-weighted MRI." Neuroimage 60.2 (2012): 1412-1425.
10. Ferizi, Uran, et al. "White matter compartment models for in vivo diffusion MRI at 300 mT/m." NeuroImage 118 (2015): 468-483.
11. Jelescu, Ileana O., et al. "Degeneracy in model parameter estimation for multi‐compartmental diffusion in neuronal tissue." NMR in Biomedicine 29.1 (2016): 33-47.
12. Kroenke, Christopher D., Joseph JH Ackerman, and Dmitriy A. Yablonskiy. "On the nature of the NAA diffusion attenuated MR signal in the central nervous system." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 52.5 (2004): 1052-1059.
13. Fieremans, Els, Jens H. Jensen, and Joseph A. Helpern. "White matter characterization with diffusional kurtosis imaging." Neuroimage 58.1 (2011): 177-188.
14. Jespersen, Sune Nørhøj, et al. "Diffusion time dependence of microstructural parameters in fixed spinal cord." Neuroimage 182 (2018): 329-342.
15. Kaden, Enrico, et al. "Multi-compartment microscopic diffusion imaging." NeuroImage 139 (2016): 346-359.
16. Reisert, Marco, et al. "Disentangling micro from mesostructure by diffusion MRI: a Bayesian approach." Neuroimage 147 (2017): 964-975.
17. Polman, Chris H., et al. "Diagnostic criteria for multiple sclerosis: 2010 revisions to the McDonald criteria." Annals of neurology 69.2 (2011): 292-302.
18. Ades-Aron, Benjamin, et al. "Evaluation of the accuracy and precision of the diffusion parameter EStImation with Gibbs and NoisE removal pipeline." NeuroImage 183 (2018): 532-543.
19. Veraart, Jelle, et al. "Denoising of diffusion MRI using random matrix theory." Neuroimage 142 (2016): 394-406.
20. Lee, Hong‐Hsi, Dmitry S. Novikov, and Els Fieremans. "Removal of partial Fourier‐induced Gibbs (RPG) ringing artifacts in MRI." Magnetic Resonance in Medicine (2021).
21. Andersson, Jesper LR, and Stamatios N. Sotiropoulos. "An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging." Neuroimage 125 (2016): 1063-1078.
22. Mori, Susumu, et al. MRI atlas of human white matter. Elsevier, 2005.
23. Sahin, Sevim, et al. "White Matter Evaluation in Multiple Sclerosis Through Magnetic Resonance Kurtosis Imaging." Cureus 11.12 (2019).
24. de Kouchkovsky, Ivan, et al. "Quantification of normal-appearing white matter tract integrity in multiple sclerosis: a diffusion kurtosis imaging study." Journal of neurology 263.6 (2016): 1146-1155.
25. Lassmann, Hans, Wolfgang Brück, and Claudia Lucchinetti. "Heterogeneity of multiple sclerosis pathogenesis: implications for diagnosis and therapy." Trends in molecular medicine 7.3 (2001): 115-121.
26. Kornek, Barbara, et al. "Multiple sclerosis and chronic autoimmune encephalomyelitis: a comparative quantitative study of axonal injury in active, inactive, and remyelinated lesions." The American journal of pathology 157.1 (2000): 267-276.
27. Stanisz, Greg J. "Diffusion MR in biological systems: tissue compartments and exchange." Israel journal of chemistry 43.1‐2 (2003): 33-44.
Figures
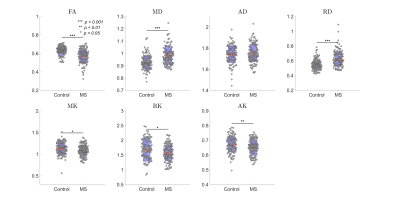
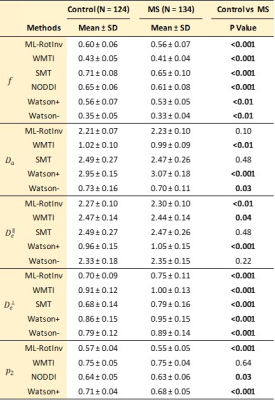
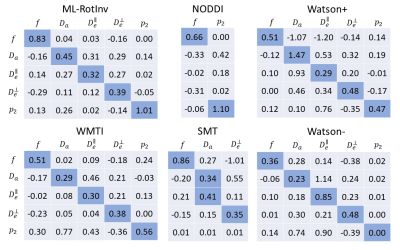
Fig. 2. Sensitivity-specificity matrix of SM parameter estimation. Each column is calculated by a linear regression of the estimation with respect to ground truth. Diagonal elements are the measure of sensitivity while the off-diagonal elements indicates specificity. Ideally, this matrix is an identity matrix, which means the change of one SM parameter in ground truth is fully captured in its own estimation with no effect on the estimation of the other parameters. Deviation from an identity matrix suggests the entanglement between parameters, especially between diffusivities.