0978
Time-dependent diffusion and kurtosis in the extra-axonal space from 3D electron microscopy substrates of injured rat brain white matter
Ricardo Coronado-Leija1, Hong-Hsi Lee2, Ali Abdollahzadeh3, Jussi Tohka3, Alejandra Sierra3, Els Fieremans1, and Dmitry S Novikov1
1Radiology, New York University School of Medicine, New York, NY, United States, 2Radiology, Massachusetts General Hospital, Harvard Medical School, Boston, MA, United States, 3University of Eastern Finland, Kuopio, Finland
1Radiology, New York University School of Medicine, New York, NY, United States, 2Radiology, Massachusetts General Hospital, Harvard Medical School, Boston, MA, United States, 3University of Eastern Finland, Kuopio, Finland
Synopsis
In this work, we perform Monte Carlo simulations of diffusion in the extra-axonal space segmented from realistic 3D electron microscopy substrates. Simulations in sham and TBI rat brains confirm the universality of the power-law functional form of the axial and radial time-dependent diffusion $$$D^{\parallel,\perp}(t)$$$ and kurtosis $$$K^{\parallel,\perp}(t)$$$. We characterize the changes caused by TBI, finding that the dependence of long-time asysmptote $$$D^{\perp}_\infty$$$ on the extra-axonal volume fraction follows Archie's law. We also validate the theoretically predicted relationship between the power-law tails of $$$D(t)$$$ and $$$K(t)$$$.
Introduction
Evidence of time-dependent diffusion $$$D(t)$$$ and kurtosis $$$K(t)$$$ in brain white and gray matter has been found in several studies1-8. Using Monte Carlo (MC) simulations, $$$D(t)$$$ was shown to provide information about structural changes caused by pathological conditions including beading9,10, axon loss11-13, demyelination11-14, and inflammation15.MC simulations in the realistic 3D extra-axonal space (EAS) have been lacking so far due to challenges in EAS segmentation. Here we, for the first time, provide MC validation of theoretical predictions for EAS $$$D(t)$$$ and $$$K(t)$$$ in realistic substrates obtained from 3D electron microscopy (EM) brain white matter segmentation of rats after sham or Traumatic Brain Injury (TBI) operations. We study the relationship between long-time asysmptote $$$D^{\perp}_\infty$$$ and the extra-axonal volume fraction, and also characterize the changes in the parameters of $$$D(t)$$$ and $$$K(t)$$$ caused by TBI.
Theory
Parallel to the axons, the theoretical prediction is9,16$$D^{||}(t)=D^{||}_\infty+\frac{c_{D^{||}}}{\sqrt{t}}\qquad(1)$$
$$K^{||}(t)=K^{||}_\infty+\frac{c_{K^{||}}}{\sqrt{t}}\qquad(2)$$
with $$$K^{||}_\infty=0$$$. Using MC simulations in axons segmented from 3D EM, Equations (1)-(2) were validated for the intra-axonal space (IAS), and their parameters were shown to be sensitive to axon caliber variation and beading9,10,17. However, the predicted power-laws for $$$D^{||}(t)$$$ and $$$K^{||}(t)$$$ have so far not been validated for the EAS in realistic substrates.
For the EAS, transverse to fibers the theoretical prediction is18
$$D^{\perp}(t)=D^{\perp}_\infty+c_{D^{\perp}}\frac{ln(t/t_c)}{t}\qquad(3)$$
$$K^{\perp}(t)=K^{\perp}_\infty+c_{K^{\perp}}\frac{ln(t/t_c)}{t}\qquad(4)$$
with $$$K^{\bot}_\infty=0$$$. Using MC simulations in-between packed cylinders and in 2D realistic substrates, $$$D^{\perp}(t)$$$ was validated, and its parameters were shown to be sensitive to structural changes caused by axonal loss and demyelination, potentially able to differentiate between them11-14.
The power-law tails of $$$D(t)$$$ and $$$K(t)$$$ are predicted to be related:3,18,19
$$K(t)=C\frac{ D(t)-D_{\infty} }{ D_{\infty} }\qquad(5)$$
with $$$C^{||}=2$$$ and $$$C^{\perp}=6$$$.
Finally, the empirical Archie’s law20 for $$$t\to\infty$$$ transverse diffusivity is
$$\frac{D^{\perp}_\infty}{D_0}=\alpha \times\mathrm{EAS}^\beta\qquad(6)$$.
Mean-field theory21,22 predicts $$$\alpha=1$$$ and $$$\beta=1$$$.
Methods
Animal preparation: TBI was induced by a lateral fluid-percussion injury in three adult rats, while two rats went through a sham-operation that included all the surgical procedures except the impact. Tissue preparation and imaging occurred five months after TBI or sham operations23,24.3D-EM Imaging: Ten white matter samples, two of each rat, extracted from the ipsi- and contralateral hemispheres of the brain, were prepared for serial block-face scanning EM imaging23,24. Large tissue volumes of 200x100x65 $$$\mu$$$m3 were imaged with a voxel size of 50×50×50 nm3. Two-thirds of the acquired samples correspond to the corpus callosum (CC) and one-third to the cingulum (CG).
Creation of substrates from 3D EM: Myelin and myelinated axons were automatically segmented using the deep-learning-based pipeline DeepACSON25,26. The segmented volumes27 were cropped into smaller volumes of 30x30x30 $$$\mu$$$m3 for each region: CC and CG, in the ipsi- and contralateral hemispheres for each of the 5 rats, making this a total of 20 substrates. Because of the low resolution of the 3D EM, the segmented myelin mask of all the axons is artificially connected, which creates spurious pockets that act as restricted pools for the diffusion of the random walkers. For this reason, watershed segmentation was used to create passages between the axons so the walkers could escape these pools. As these passages traverse voxels previously filled by myelin mask, substrates with different voxel sizes: 20, 30, 40 and 50 nm isotropic were created to test the effect of the width of these passages.
MC Simulations: MC simulations were performed using the realistic microstructure simulator28(RMS), which allows to simulate in a voxelated geometry. These simulations were done using $$$8\times10^6$$$ random walkers, $$$D_0=D(t=0)=2$$$ ms/$$$\mu$$$m2, total diffusion time of 100 ms, with time step=0.000027 ms (length step=18 nm).
Results
Figure 1 shows sham and TBI examples of substrates created from the segmentation of 3D EM; differences in the EAS can be observed.The universality of Equations (1)-(4) is shown in Figure 2, these long-time-limit functional forms are followed for all cases: TBI, sham, substrates created with and without passages between the axons, and for different widths of theses passages caused by the change to substrate resolution.
As shown in Figure 3, the differences between the change to substrate structures are captured by the parameters of Equations (1)-(4), the changes in $$$c_{D^{\bot}}$$$ and $$$D^{\bot}_\infty$$$ are similar to those found in models for demyelination11-13, which is expected as myelin is removed when creating the passages.
$$$C^{||}=2$$$ in Equation (5) is followed for most cases as shown in Figure 4. It may be needed to simulate longer times to validate $$$C^{\perp}=6$$$.
Changes caused by TBI in several parameters can be observed in Figure 5. Interestingly, the right panel shows that $$$D^{\bot}_\infty$$$ approximately follows Equation (6) with $$$\alpha=1,\beta=1$$$ for $$$\mathrm{EAS}>0.3$$$.
Conclusions
In this work, we validate the power-laws for the axial and radial $$$D(t)$$$ and $$$K(t)$$$ in the EAS using realistic substrates obtained from 3D EM of sham and TBI-operated rats. We also confirm the relation between the power-law tails of $$$D^{||}(t)$$$ and $$$K^{||}(t)$$$ and show the sensitivity of parameters obtained from $$$D(t)$$$ and $$$K(t)$$$ to TBI.Remarkably, we observe that $$$D^{\perp}_\infty$$$ follows mean-field theory prediction for EAS fractions > 0.3. Assuming cylindrical shapes for axons, this prediction is only valid21,22 for EAS fractions > 0.6, which emphasizes the need for realistic simulations in tissue microstructure to interpret dMRI measurements.
Acknowledgements
Research was supported by the National Institute of Neurological Disorders and Stroke of the NIH under awards R01 NS088040 and R21 NS081230, and by the Hirschl foundation, and was performed at the Center of Advanced Imaging Innovation and Research (CAI2R, www.cai2r.net), a Biomedical Technology Resource Center supported by NIBIB with the award P41 EB017183. A.S. was supported by the Academy of Finland (grant #323385) and the Erkko Foundation. H.H.L was supported by the Office of the Director of the NIH under award DP5 OD031854.References
1. MA Horsfield, GJ Barker, WI McDonald. Self-diffusion in CNS tissue by volume-selective proton NMR. Magn Reson Med. 1994;31:637-644.
2. Els Fieremans, Lauren M Burcaw, Hong-Hsi Lee, Gregory Lemberskiy, Jelle Veraart, Dmitry S Novikov. In vivo observation and biophysical interpretation of time-dependent diffusion in human white matter. Neuroimage. 2016;129:414-427.
3. Hong-Hsi Lee, Antonios Papaioannou, Sung-Lyoung Kim, Dmitry S Novikov, Els Fieremans. In vivo observation and biophysical interpretation of time-dependent diffusion in human cortical gray matter. Neuroimage. 2020;222:117054
4. S De Santis, DK Jones, A Roebroeck. Including diffusion time dependence in the extra-axonal space improves in vivo estimates of axonal diameter and density in human white matter. NeuroImage. 2016;130:91-103.16.
5. CA Baron, C Beaulieu. Oscillating gradient spin-echo (OGSE) diffusion tensor imaging of the human brain. Magn Reson Med. 2014;72:726-736.
6. Manisha Aggarwal, Matthew D Smith, Peter A Calabresi. Diffusion-time dependence of diffusional kurtosis in the mouse brain. Magn Reson Med. 2020;84(3):1564-1578.
7. Ileana O. Jelescu, Alexandre de Skowronski, Marco Palombo, Dmitry S. Novikov. Neurite Exchange Imaging (NEXI): A minimal model of diffusion in gray matter with inter-compartment water exchange. Arxiv preprint, 2021.
8. Jonas L. Olesen, Leif Østergaard, Noam Shemesh, Sune N. Jespersen. Diffusion time dependence, power-law scaling, and exchange in gray matter. Arvix 2021
9. Hong-Hsi Lee, Antonios Papaioannou, Sung-Lyoung Kim, Dmitry S Novikov, Els Fieremans. A time-dependent diffusion MRI signature of axon caliber variations and beading. Commun Biol. 2020;3(1):354.
10. Matthew D Budde, Joseph A Frank. Neurite beading is suficient to decrease the apparent diffusion coeficient after ischemic stroke. Proc Natl Acad Sci. 2010;107(32):14472-7
11. E. Fieremans, J. H. Jensen, J. Helpern, S. Kim, R. Grossman, M. Inglese, D. Novikov. Diffusion distinguishes between axonal loss and demyelination in brain white matter. Proc. Intl. Soc. Mag. Reson. Med. 2012.
12. D. S. Novikov, E. Fieremans. Relating extracellular diffusivity to cell size distribution and packing density as applied to white matter. Proc. Intl. Soc. Mag. Reson. Med. 2012
13. Ricardo Coronado-Leija, Hong-Hsi Lee, Els Fieremans, and Dmitry S. Novikov. Characterizing time-dependent diffusion in the extra-axonal space of white matter for axon loss and demyelination. Proc. ISMRM 3402, 2021.
14. Ginsburger Kévin, Poupon Fabrice, Beaujoin Justine, Estournet Delphine, Matuschke Felix, Mangin Jean-François, Axer Markus, Poupon Cyril. Improving the Realism of White Matter Numerical Phantoms: A Step toward a Better Understanding of the Influence of Structural Disorders in Di!usion MRI. Frontiers in Physics. 2018;6.
15. Döring, André Afzali, Maryam Kleban, Elena Kreis, Roland Jones, Derek. Realistic simulations of diffusion MR spectroscopy: The effect of glial cell swelling on non-Gaussian and anomalous diffusion. Proc ISMRM 2021
16. Dmitry S Novikov, Jens H Jensen, Joseph A Helpern, Els Fieremans. Revealing mesoscopic structural universality with diffusion. Proc Natl Acad Sci USA. 2014;111(14):5088-93.3.
17. Hong-Hsi Lee, Katarina Yaros, Jelle Veraart, Jasmine L Pathan, Feng-Xia Liang, Sungheon G Kim, Dmitry S Novikov, Els Fieremans. Along-axon diameter variation and axonal orientation dispersion revealed with 3D electron microscopy: implications for quantifying brain white matter microstructure with histology and diffusion MRI. Brain Struct Funct. 2019;224(4):1469-1488.
18. Lauren M Burcaw, Els Fieremans, Dmitry S Novikov. Mesoscopic structure of neuronal tracts from time-dependent diffusion. Neuroimage. 2015;114:18-37.
19. Bibek Dhital, Elias Kellner, Valerij G Kiselev, Marco Reisert. The absence of restricted water pool in brain white matter. Neuroimage 2018 15;182:398-406.
20. Archie, G E.. 1942. The electrical resistivity log as an aid in determining some reservoir characteristics: Trans. AIME. v. 146. p. 53-62.
21. DAG Bruggeman, Ann Phys (Leipzig) 24 (1935) 636.
22. P. N. Sen, C. Scala, and M. H. Cohen. A self-similar model for sedimentary rocks with application to the dielectric constant of fused glass beads. Geophysics 46 (1981) 781.
23. Raimo A. Salo, Ilya Belevich, Eppu Manninen, Eija Jokitalo, Olli Gröhn, Alejandra Sierra. Quantification of anisotropy and orientation in 3D electron microscopy and diffusion tensor imaging in injured rat brain. NeuroImage 2018.172: 404-414
24. Raimo A. Salo, Ilya Belevich, Eija Jokitalo, Olli Gröhn, Alejandra Sierra. Assessment of the structural complexity of diffusion MRI voxels using 3D electron microscopy in the rat brain. 2021. NeuroImage 225.
25. Ali Abdollahzadeh, Ilya Belevich, Eija Jokitalo, Jussi Tohka, Alejandra Sierra. Automated 3D Axonal Morphometry of White Matter. Sci Rep. 2019 Apr 15;9(1):6084.
26. Ali Abdollahzadeh, Ilya Belevich, Eija Jokitalo, Alejandra Sierra, Jussi Tohka. DeepACSON automated segmentation of white matter in 3D electron microscopy. Commun Biol. 2021 Feb 10;4(1):179.
27. Abdollahzadeh, A., Belevich, I., Jokitalo, E., Tohka, J. & Sierra, A. Segmentation of white matter ultrastructures in 3D electron microscopy. 2020
28. Hong-Hsi Lee, Els Fieremans, Dmitry S Novikov. Realistic Microstructure Simulator (RMS): Monte Carlo simulations of diffusion in three-dimensional cell segmentations of microscopy images. J Neurosci Methods. 2021;350:109018.
2. Els Fieremans, Lauren M Burcaw, Hong-Hsi Lee, Gregory Lemberskiy, Jelle Veraart, Dmitry S Novikov. In vivo observation and biophysical interpretation of time-dependent diffusion in human white matter. Neuroimage. 2016;129:414-427.
3. Hong-Hsi Lee, Antonios Papaioannou, Sung-Lyoung Kim, Dmitry S Novikov, Els Fieremans. In vivo observation and biophysical interpretation of time-dependent diffusion in human cortical gray matter. Neuroimage. 2020;222:117054
4. S De Santis, DK Jones, A Roebroeck. Including diffusion time dependence in the extra-axonal space improves in vivo estimates of axonal diameter and density in human white matter. NeuroImage. 2016;130:91-103.16.
5. CA Baron, C Beaulieu. Oscillating gradient spin-echo (OGSE) diffusion tensor imaging of the human brain. Magn Reson Med. 2014;72:726-736.
6. Manisha Aggarwal, Matthew D Smith, Peter A Calabresi. Diffusion-time dependence of diffusional kurtosis in the mouse brain. Magn Reson Med. 2020;84(3):1564-1578.
7. Ileana O. Jelescu, Alexandre de Skowronski, Marco Palombo, Dmitry S. Novikov. Neurite Exchange Imaging (NEXI): A minimal model of diffusion in gray matter with inter-compartment water exchange. Arxiv preprint, 2021.
8. Jonas L. Olesen, Leif Østergaard, Noam Shemesh, Sune N. Jespersen. Diffusion time dependence, power-law scaling, and exchange in gray matter. Arvix 2021
9. Hong-Hsi Lee, Antonios Papaioannou, Sung-Lyoung Kim, Dmitry S Novikov, Els Fieremans. A time-dependent diffusion MRI signature of axon caliber variations and beading. Commun Biol. 2020;3(1):354.
10. Matthew D Budde, Joseph A Frank. Neurite beading is suficient to decrease the apparent diffusion coeficient after ischemic stroke. Proc Natl Acad Sci. 2010;107(32):14472-7
11. E. Fieremans, J. H. Jensen, J. Helpern, S. Kim, R. Grossman, M. Inglese, D. Novikov. Diffusion distinguishes between axonal loss and demyelination in brain white matter. Proc. Intl. Soc. Mag. Reson. Med. 2012.
12. D. S. Novikov, E. Fieremans. Relating extracellular diffusivity to cell size distribution and packing density as applied to white matter. Proc. Intl. Soc. Mag. Reson. Med. 2012
13. Ricardo Coronado-Leija, Hong-Hsi Lee, Els Fieremans, and Dmitry S. Novikov. Characterizing time-dependent diffusion in the extra-axonal space of white matter for axon loss and demyelination. Proc. ISMRM 3402, 2021.
14. Ginsburger Kévin, Poupon Fabrice, Beaujoin Justine, Estournet Delphine, Matuschke Felix, Mangin Jean-François, Axer Markus, Poupon Cyril. Improving the Realism of White Matter Numerical Phantoms: A Step toward a Better Understanding of the Influence of Structural Disorders in Di!usion MRI. Frontiers in Physics. 2018;6.
15. Döring, André Afzali, Maryam Kleban, Elena Kreis, Roland Jones, Derek. Realistic simulations of diffusion MR spectroscopy: The effect of glial cell swelling on non-Gaussian and anomalous diffusion. Proc ISMRM 2021
16. Dmitry S Novikov, Jens H Jensen, Joseph A Helpern, Els Fieremans. Revealing mesoscopic structural universality with diffusion. Proc Natl Acad Sci USA. 2014;111(14):5088-93.3.
17. Hong-Hsi Lee, Katarina Yaros, Jelle Veraart, Jasmine L Pathan, Feng-Xia Liang, Sungheon G Kim, Dmitry S Novikov, Els Fieremans. Along-axon diameter variation and axonal orientation dispersion revealed with 3D electron microscopy: implications for quantifying brain white matter microstructure with histology and diffusion MRI. Brain Struct Funct. 2019;224(4):1469-1488.
18. Lauren M Burcaw, Els Fieremans, Dmitry S Novikov. Mesoscopic structure of neuronal tracts from time-dependent diffusion. Neuroimage. 2015;114:18-37.
19. Bibek Dhital, Elias Kellner, Valerij G Kiselev, Marco Reisert. The absence of restricted water pool in brain white matter. Neuroimage 2018 15;182:398-406.
20. Archie, G E.. 1942. The electrical resistivity log as an aid in determining some reservoir characteristics: Trans. AIME. v. 146. p. 53-62.
21. DAG Bruggeman, Ann Phys (Leipzig) 24 (1935) 636.
22. P. N. Sen, C. Scala, and M. H. Cohen. A self-similar model for sedimentary rocks with application to the dielectric constant of fused glass beads. Geophysics 46 (1981) 781.
23. Raimo A. Salo, Ilya Belevich, Eppu Manninen, Eija Jokitalo, Olli Gröhn, Alejandra Sierra. Quantification of anisotropy and orientation in 3D electron microscopy and diffusion tensor imaging in injured rat brain. NeuroImage 2018.172: 404-414
24. Raimo A. Salo, Ilya Belevich, Eija Jokitalo, Olli Gröhn, Alejandra Sierra. Assessment of the structural complexity of diffusion MRI voxels using 3D electron microscopy in the rat brain. 2021. NeuroImage 225.
25. Ali Abdollahzadeh, Ilya Belevich, Eija Jokitalo, Jussi Tohka, Alejandra Sierra. Automated 3D Axonal Morphometry of White Matter. Sci Rep. 2019 Apr 15;9(1):6084.
26. Ali Abdollahzadeh, Ilya Belevich, Eija Jokitalo, Alejandra Sierra, Jussi Tohka. DeepACSON automated segmentation of white matter in 3D electron microscopy. Commun Biol. 2021 Feb 10;4(1):179.
27. Abdollahzadeh, A., Belevich, I., Jokitalo, E., Tohka, J. & Sierra, A. Segmentation of white matter ultrastructures in 3D electron microscopy. 2020
28. Hong-Hsi Lee, Els Fieremans, Dmitry S Novikov. Realistic Microstructure Simulator (RMS): Monte Carlo simulations of diffusion in three-dimensional cell segmentations of microscopy images. J Neurosci Methods. 2021;350:109018.
Figures
Figure 1. Sham (top) and TBI (bottom) examples of realistic substrates obtained from 3D EM of the cingulum. Left: 3D EM slices. Middle: segmented IAS, EAS, and Myelin. Right: 3D visualization of the segmented axons in the cingulum. Changes caused by TBI can be observed in the increase of the EAS and the smaller axon diameters with respect to the sham.
Figure 2. Extra-axonal $$$D(t)^{||}$$$, $$$K(t)^{||}$$$, $$$K(t)^{\perp}$$$ and $$$D(t)^{\perp}$$$ follow their power-law functional forms in the long time limit. The universality of the power-laws can be observed as $$$D(t)$$$ and $$$K(t)$$$ follow their functional forms for both TBI and sham, with and without the creation of passages, and for the different widths of the passages caused by the different resolution. The differences between all these substrates are captured by changes in the parameters of $$$D(t)$$$ and $$$K(t)$$$, showing their sensitivity to microgeometry.
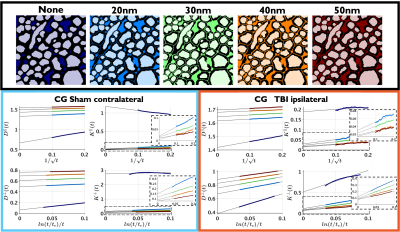
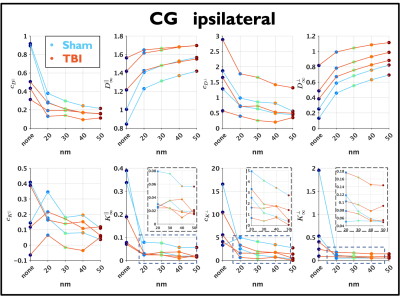
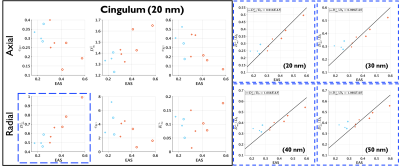
Figure 3. Changes of the parameters of $$$D(t)^{||}$$$, $$$K(t)^{||}$$$, $$$K(t)^{\perp}$$$ and $$$D(t)^{\perp}$$$ due to the different widths of the passages (resolution of the substrates). The decrease in $$$c_{D^{\perp}}$$$ and the increase in $$$D^{\perp}_\infty$$$ are consistent with models of demyelination, which is expected as the passages were created in voxels previously occupied by myelin, and by increasing the voxel size more myelin is removed.
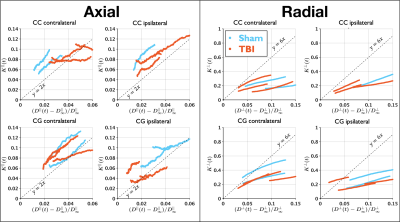
Figure 4. Relation between the power-law tails in $$$D(t)$$$ and $$$K(t)$$$ on 20 nm substrates. In the axial direction, it can be observed that for most cases Equation 5 approaches the $$$y=2x$$$ reference line, the translations observed on the different lines are caused by non-zero $$$K^{||}_\infty$$$. In the radial direction, the $$$y=6x$$$ reference line (Equation (5), $$$C^{\perp}$$$) does not hold, possibly since $$$D(t)$$$ and $$$K(t)$$$ are not in the long-time limit yet, but the prediction seems to be valid in the contra-lateral sides.
Figure 5. Left: Changes on axial and radial $$$D(t)$$$ and $$$K(t)$$$ parameters in the cingulum, caused by TBI, plotted with respect to changes in the EAS in 20 nm substrates. In particular increases of $$$D^{||}_\infty$$$ and $$$D^{\perp}_\infty$$$ and decreases in $$$c_{D^{||}}$$$ are evident. Right: $$$D^{\perp}_\infty$$$ approximately follows the mean-field theory prediction, Eq(6),with $$$\alpha=1$$$ and $$$\beta=1$$$ for EAS>0.3.
DOI: https://doi.org/10.58530/2022/0978