0976

Characterisation of restricted diffusion and exchange using the velocity autocorrelation function

Arthur Chakwizira¹, Samo Lasič², Alexis Reymbaut³, Carl-Fredrik Westin⁴, Filip Szczepankiewicz⁵, and Markus Nilsson⁵
¹Medical Radiation Physics, Lund, Lund University, Lund, Sweden, ²Danish Research Centre for Magnetic Resonance, Centre for Functional and Diagnostic Imaging and Research, Copenhagen University Hospital, Amager and Hvidovre, Copenhagen, Denmark, ³Random Walk Imaging, AB, Lund, Sweden, ⁴Department of Radiology, Brigham and Women's hospital, Harvard Medical School, Boston, MA, United States, ⁵Clinical Sciences Lund, Lund University, Lund, Sweden

Synopsis

Temporal velocity correlations of diffusing particles carry information about the structure of the diffusion environment. Studying high-order velocity autocorrelation functions can aid in understanding how signal is influenced by restricted diffusion and exchange, and in turn how to design experiments that are sensitive/independent to these phenomena. In this work, we employ numerical simulations on a variety of substrates to demonstrate this notion. We find that the fourth order velocity autocorrelation bears a distinctive signature of exchanging systems. In addition, we highlight that the effect of exchange on the second order velocity autocorrelation is negligible when exchange is barrier-limited.

Introduction

Particles undergoing diffusion exhibit temporal velocity correlations that carry information about the environment in which the particles exist¹. The second-order velocity autocorrelation function (VAF2) carries a signature of the geometry of restriction that allows the estimation of restriction lengths via time-dependent diffusion MRI (dMRI)². However, higher order VAFs are not well-understood compared to the second order VAF. In this work, we explore the fourth-order VAF (VAF4) as a tool to characterise compartmental systems in terms of restriction and exchange. We provide a link between the VAF and the diffusion-encoding gradient waveform which allows the design of experiments that selectively probe either restriction or exchange.

Theory

Consider the cumulant expansion of the dMRI signal^1,2
$$\ln(S/S_0) \approx -\frac{1}{2}\langle \phi^2 \rangle _c + \frac{1}{24} \langle \phi^4 \rangle_c$$

where $$$ \langle \phi^2 \rangle_c $$$ and $$$ \langle \phi^4 \rangle_c $$$ are the second and fourth cumulants of the phase distribution, with the phase $$$ \phi $$$ given by
$$ \phi = - \int_0^T q(t)v(t) dt $$
where $$$q(t)$$$ is the dephasing q-vector and $$$v(t)$$$ is the particle velocity at time $$$t$$$¹. For simplicity, only the 1D case is considered here. The phase cumulants are then given by
$$ \langle \phi^2 \rangle_c = \int_0^T\int_0^T q(t_1)q(t_2) \langle v(t_1)v(t_2) \rangle_c dt_1dt_2$$
$$ \langle \phi^4 \rangle_c = \int_0^T\int_0^T\int_0^T\int_0^T q(t_1)q(t_2)q(t_3)q(t_4) \langle v(t_1)v(t_2)v(t_3)v(t_4) \rangle_c dt_1dt_2dt_3dt_4$$
For convenience we replace $$$t_1, …, t_4$$$ with indices $$$i,…,l$$$ and note that the cumulants are related to the second and fourth-order velocity autocorrelations $$$\langle v_iv_j \rangle $$$ and $$$\langle v_iv_jv_kv_l \rangle$$$ via
$$\langle v_iv_j \rangle_c = \langle v_iv_j \rangle $$
$$ \langle v_iv_jv_kv_l \rangle_c = \langle v_iv_jv_kv_l \rangle - \langle v_iv_j \rangle \langle v_kv_l \rangle - \langle v_iv_k \rangle \langle v_jv_l \rangle - \langle v_iv_l \rangle \langle v_jv_k \rangle$$
These provide a comprehensive characterisation of the microstructure.

Methods

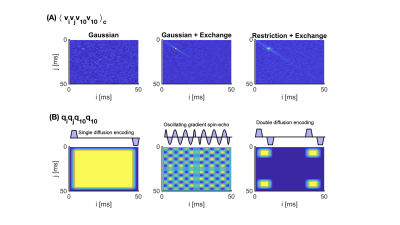
We visualise VAF2 and VAF4 in multiple microstructures based on Monte Carlo simulations in: single Gaussian pool, two Gaussian pools with and without exchange, two restricted compartments with and without exchange, one restricted and one hindered compartment with and without exchange. For the two pool/compartment cases, fractions were set to $$$0.7$$$ and $$$0.3$$$. In all cases, the bulk diffusivity was $$$2$$$ µm$$$^2$$$/ms and the velocity components along the x-axis were used to compute the VAF. Simulations were run using $$$100 000$$$ particles for $$$50$$$ ms at a time step of $$$10$$$ μs. For the VAF computation, trajectories were sampled every 1 ms.

Characterising diffusion environments using VAF4 can guide the design of gradient waveforms to probe specific features of those environments. We illustrated this by visualising both VAF4 and the encoding function $$$q_iq_jq_kq_l$$$ along the $$$iijj$$$ axis.

In complex environments, time-dependence is driven by multiple features. To separate exchange from restriction, we grouped the contributions to the phase from $$$iijj$$$ terms and studied their temporal dynamics in different systems.

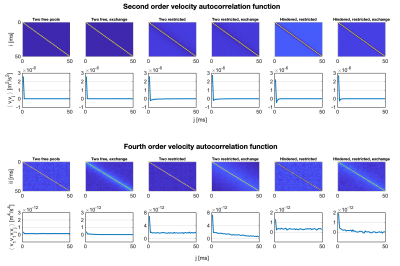
As a motivation for exploring higher order velocity correlations, we evaluated both VAF2 and VAF4 for all substrates considered and compared the exchanging to the non-exchanging cases.
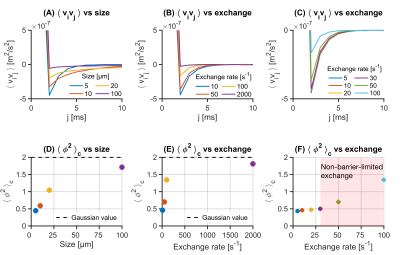
We also investigated if/when exchange manifests in VAF2.

Results

Figure 1 shows that the distribution of $$$q_iq_jq_kq_l$$$ across the different time axes determines how good a probe a given waveform is for exchange or restriction. For example, FEXI encodes along the diagonal, which is where the effect of exchange is evident.

In Fig.2, we show that the fourth cumulant can be decomposed into distinct contributions. The general effect of exchange in Fig.2 is to decrease the fourth cumulant.

Figure 3 presents VAF2 and VAF4 for all simulated environments. Environments with and without exchange appear largely identical in VAF2. In VAF4, however, the different systems exhibit different signatures.

Figure 4 shows VAF2 in the case of hindered-restricted diffusion with exchange. Generally, both growing size and increasing exchange rate tend to bring VAF2 to the single-Gaussian-pool case. However, exceptionally fast exchange is required to produce a noticeable effect on VAF2. Specifically, Fig.4 clarifies that when exchange is non-barrier-limited, it has a drastic influence on the second order VAF which can be confused with that of a growing size.

Discussion

This work has demonstrated the utility of high order velocity autocorrelations in characterising exchanging diffusion environments. Systems identical in the second order VAF can be vastly different in their fourth order VAF (Fig. 3). Understanding the mechanisms of restriction and exchange facilitates the design of experiments to target specific aspects of the microstructure (Fig.1), which can help to disentangle the effects of restriction and exchange on the diffusion weighted signal^5,6,7. We found that exchange dominates where time points in the set $$$[t_1, t_2, t_3, t_4]$$$ are pairwise equal. The encoding function along this axis is the exchange-weighting function presented in previous work⁴. Furthermore, we explored a revealing decomposition of the fourth phase cumulant into a Gaussian/exchange and a restricted component (Fig. 2). This concept can be related to correlation tensor imaging (CTI)⁸where different kurtosis components (isotropic, non-isotropic and microscopic) are resolved, with the distinction that CTI does not consider exchange. In conclusion, studying high order velocity autocorrelation functions can provide valuable insights about diffusion in complex environments.

Acknowledgements

No acknowledgement found.

References

1. Stepišnik J. Time-dependent self-diffusion by NMR spin-echo. Physica B: Condensed Matter. 1993 May 1;183(4):343–502.

2. Reynaud O. Time-Dependent Diffusion MRI in Cancer: Tissue Modeling and Appli- cations. Front Phys. 2017 Nov;5

3. Stepisnik J. Validity limits of Gaussian approximation in cumulant expansion for diffusion attenuation of spin echo. Physica B. 1999;270:110-117

4. Ning L, Nilsson M, Lasič S, Westin C-F, Rathi Y. Cumulant expansions for measuring water exchange using diffusion MRI. J Chem Phys. 2018 Feb 21;148(7):074109

5. Price WS, Barzykin AV, Hayamizu K, Tachiya M. A Model for Diffusive Transport through a Spherical Interface Probed by Pulsed-Field Gradient NMR. Biophysical Journal. 1998 May 1;74(5):2259–71

6. Nilsson M, Westin C-F, Brabec J, Lasič S, Szczepankiewicz F. A unified framework for analysis of time-dependent diffusion: numerical validation of a restriction-exchange correlation experiment. Proceedings of ISMRM Montreal, QC, Canada. 2019

7. Olesen JL, Østergaard L, Shemesh N, Jespersen SN. Diffusion time dependence, power-law scaling, and exchange in gray matter. arXiv:210809983 [physics] [Internet]. 2021 Aug 23 [cited 2021 Oct 3]; Available from: http://arxiv.org/abs/2108.09983

8. Henriques RN, Jespersen SN, Shemesh N. Correlation tensor magnetic resonance imaging. NeuroImage. 2020 May 1;211:116605

Figures

Figure 1. Visualisation of the velocity autocorrelation function in relation to the fourth order correlation function of the dephasing q-vector. Panel A shows distinct fourth order VAFs for three environments and B shows that different waveforms probe these environments differently depending on how their encoding power is distributed across the temporal dimensions. For example, FEXI is a strong probe of exchange because it encodes along the diagonal terms where exchange is dominant.

Figure 2: Visualisation of the fourth order phase cumulant for different environments as a function of diffusion encoding time. The total cumulant encompasses effects of both restricted diffusion, free diffusion and exchange. The Gaussian+exchange component is obtained by gathering only the iijj terms of the fourth order VAF. The difference between “Total” and “Gaussian + Exchange” is attributed to restriction.

Figure 3: Comparison of second and fourth order velocity autocorrelation functions from different environments. The images show the iijj terms of the fourth order VAF. The 1-dimensional plots show a horizontal profile through the corresponding image. Systems with an identical second order VAF exhibit distinct signatures in the fourth order case. Exchange manifests as a temporal decay of the fourth order VAF.

Figure 4: Effect of exchange on the second order VAF. Both growing size and exchange rate drive the system towards Gaussian diffusion (non-negative VAF2). When exchange is barrier-limited, it does not influence the second order VAF (panel F).

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

0976

DOI: https://doi.org/10.58530/2022/0976