0963
Multi-domain Motion Correction Network for Turbo Spin-echo MRI
Jongyeon Lee1, Wonil Lee1, Namho Jeong1, and HyunWook Park1
1Korea Advanced Institute of Science and Technology, Daejeon, Korea, Republic of
1Korea Advanced Institute of Science and Technology, Daejeon, Korea, Republic of
Synopsis
Motion correction in MRI has been successfully performed by adopting deep learning techniques to correct motion artifacts with data-driven algorithms. However, many of these studies have narrowly utilized MR physics. In addition to the efficient motion correction method proposed for multi-contrast MRI, we expand our previous method to utilize data in k-space domain for a single-contrast MRI. Using the motion simulation based on MR physics, we propose a multi-domain motion correction method in both k-space and image domains. Our proposed method finely reduces motion artifacts using the multi-domain network.
Introduction
Motion correction techniques have been studied to remove or reduce motion artifacts, which are caused by subject movement during scanning. Most of the techniques require extra motion information for motion estimation and have a cost of a prolonged scan time1. Recently, deep learning algorithms have been adopted to correct the artifacts in MR images without motion estimation2,3.While motion artifacts are caused by inconsistency of motion states among k-space lines, deep learning techniques also can be applied in k-space domain. There have been some studies that utilize k-space domain for dynamic imaging4 and accelerated MRI5,6.
To fully utilize the given data in both domains, we propose a multi-domain motion correction network, which consists of two CNNs in the k-space and image domains. The network in the k-space domain is designed to roughly interpolate zero-padded data for each segment. These weakly interpolated k-space data are Fourier transformed into the image domain and the image domain network gathers these ill-reconstructed image data and refines them into motion-corrected images.
Methods
MR brain images are acquired with a T2w turbo spin-echo sequence. For training data, we obtain 3D T2w data to simulate in-plane and through-plane motion artifacts because through-plane motions cannot be simulated with 2D data. We apply Fourier transform to 3D k-space data along with the slice direction to convert 3D data into 2D data of thin slices. Then, we randomly simulate motions for k-space segments to efficiently generate the training data with a limited number of subjects. Training data are 2560 slices from 10 subjects and test data are 768 slices from 3 subjects, which were acquired at 3T scanner (Verio, Siemens).Let $$$y_{\text{gt},i}$$$ is the acquired MR image for $$$i$$$-th channel coil, $$$i\in[1,N]$$$, where $$$N$$$ is the number of coil channels (32 in this study). As the turbo spin-echo sequence consists of interleaved segments, the corresponding binary mask for each segment is defined by $$$m_j$$$ where $$$j\in[1,M]$$$ and $$$M$$$ is the number of shots used for the sequence (16 in this study). An input k-space data of $$$i$$$-th channel coil and $$$j$$$-th segment is defined as $$x_{i,j}=(S_j𝓕y_{\text{gt},i})\odot m_j$$ where 𝓕 is Fourier transform operator, $$$\odot$$$ is the Hadamard product operator, and $$$S_j$$$ is the random motion simulation model for the segment $$$j$$$. The motion simulation follows Lee’s method2 for T2w turbo spin-echo images. To simulate motion artifacts, we set that $$$S_j$$$ randomly changes at least twice and at most six times in a whole scan. A sum of the input k-space data can be inversely Fourier transformed into motion-corrupted MR image as $$y_{\text{mot},i}=𝓕^{-1}\left[\sum_{j=1}^{M}{x_{i,j}}\right].$$ We set output of the network in k-space domain as fully interpolated k-space data for each segment as $$\text{Net}_{\text{K}}([x_{i,1},\cdots,x_{i,j},\cdots,x_{i,M}])=[\hat{x}_{i,1},\cdots,\hat{x}_{i,k},\cdots,\hat{x}_{i,M}],$$ where $$$\hat{x}_{i,k}$$$ is the $$$k$$$-th network channel of the output of the k-space network, where $$$k\in[1,M]$$$. For a real implementation, we apply an annihilating filter5 to emphasize peripheral signals of low intensities. It is impossible to interpolate the full k-space data from zero-padded data of each channel. Therefore, we expect that they can be roughly reconstructed by referring data in other channels. A loss function for k-space data, $$$𝓛_{\text{K}}$$$, and a loss function for their image domain loss, $$$𝓛_{\text{I,1}}$$$, are defined as $$𝓛_{\text{K}}=\sum_{j=k=1}^{M}{\Vert\hat{x}_{i,k}-S_j𝓕y_{\text{gt},i}\Vert_{2}^{2}},$$ $$𝓛_{\text{I,1}}=\sum_{j=k=1}^{M}{\vert𝓕^{-1}\hat{x}_{i,k}-𝓕^{-1}S_j𝓕y_{\text{gt},i}\vert}.$$
The network in the image domain for final reconstruction of motion-corrected images receives an input images of $$$M$$$ channels and aims to reconstruct a motion-corrected image, $$$\hat{y}_i$$$, for each batch as $$\text{Net}_{\text{I}}([𝓕^{-1}\hat{x}_{i,1},\cdots,\hat{x}_{i,k},\cdots,𝓕^{-1}\hat{x}_{i,M}])=\hat{y}_i.$$ A loss function is the mean absolute error as $$𝓛_{\text{I,2}}=\vert\hat{y}_{i}-𝓕^{-1}S_{M/2}𝓕y_{\text{gt},i}\vert,$$ where $$$M/2$$$ means the segment containing the center k-space line so that the target ground truth image is set as the motion-less image, whose pose is determined by the center k-space line.
For the interpolation network in k-space domain, we employ the complex convolution3 to deal with complex k-space data to make kernels complex. The image domain network is based on the ResNet generator7. The motion simulation method of the proposed method is illustrated in Figure 1 and the implementation of the deep network is explained in Figure 2.
Considering intensity levels, we combine three loss functions, where the final loss $$$𝓛$$$ is defined as $$$𝓛=\lambda_{\text{K}}𝓛_{\text{K}}+\lambda_{\text{I,1}}𝓛_{\text{I,1}}+\lambda_{\text{I,2}}𝓛_{\text{I,2}}$$$. Adam optimizer is used for the optimization with the learning rate of $$$10^{-4}$$$. After all channel images are corrected, we reconstruct a final motion-corrected MR image by the sum-of-squares of the multi-channel motion-corrected images.
Experiments and Results
To analyze our contributions, we set several experiments with different loss weights. Table 1 shows the results of the evaluation on the synthesized motion-corrupted datasets. It shows that our proposed method yields the best metrics when $$$\lambda_{\text{K}}=1, \lambda_{\text{I,1}}=0$$$, and $$$\lambda_{\text{I,2}}=100$$$. It reveals that the interpolation network in k-space domain helps to reduce motion artifacts, but the image domain loss on its output data is unnecessary. Figure 3 shows the several motion-corrected images from the motion-simulated datasets.Discussion and Conclusion
As this study is only tested on the motion-simulated datasets, we should further apply the method to real motion-corrupted 2D images. Furthermore, we need to adjust the loss weights of the final loss function and find more appropriate loss functions to increase its performances.We proposed the multi-domain motion correction network and the proposed method reduced motion artifacts and showed its potential to correct through-plane motion artifacts.
Acknowledgements
This research was partly supported by a grant of the Korea Health Technology R&D Project through the Korea Health Industry Development Institute (KHIDI), funded by the Ministry of Health & Welfare, Republic of Korea (grant number: HI14C1135). This work was also partly supported by Institute for Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (No.2017-0-01779, A machine learning and statistical inference framework for explainable artificial intelligence).References
- Zaitsev M, Maclaren J, Herbst M. Motion artifacts in MRI: A complex problem with many partial solutions. Journal of Magnetic Resonance Imaging. 2015;42(4):887-901.
- Lee J, Kim B, Park H. MC2‐Net: motion correction network for multi‐contrast brain MRI. Magnetic Resonance in Medicine. 2021;86(2):1077-1092.
- Usman M, Latif S, Asim M, et al. Retrospective motion correction in multishot MRI using generative adversarial network. Scientific Reports. 2020;10(1):1-11.
- El‐Rewaidy H, Fahmy AS, Pashakhanloo F, et al. Multi‐domain convolutional neural network (MD‐CNN) for radial reconstruction of dynamic cardiac MRI. Magnetic Resonance in Medicine. 2021;85(3):1195-1208.
- Han Y, Sunwoo L, Ye JC. k-Space Deep Learning for Accelerated MRI. IEEE Transactions on Medical Imaging. 2019;39(2):377-386.
- Sriram A, Zbontar J, Murrell T, et al. GrappaNet: Combining parallel imaging with deep learning for multi-coil MRI reconstruction. In Proceedings of the CVPR 2020:14315-14322.
- Zhu JY, Park T, Isola P, Efros AA. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the ICCV 2017:2223-2232.
Figures
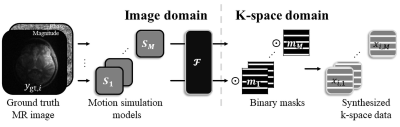
Figure 1. Synthesis
of k-space data with simulated motions. The k-space data are generated by
random motion simulation models and by multiplying binary masks. The synthesized
k-space data become the input data for the multi-domain motion correction
network.
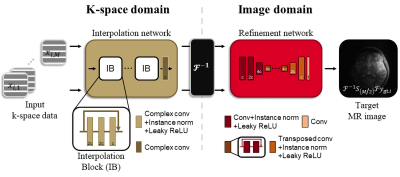
Figure 2. Proposed multi-domain motion correction network.
Complex convolutional layers are used for the interpolation network with a
kernel size of three and the six interpolation blocks. The refinement network
uses real-valued convolutional layers with a kernel size of three except for
the first and the last layers with a kernel size seven. Downsampling and
upsampling layers use a stride of two and six residual blocks are used.
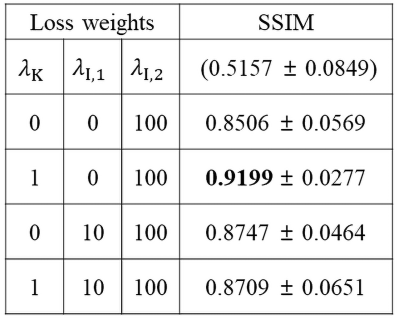
Table 1. Quantitative results with SSIM
for the synthesized test datasets with different loss weight settings. The
values in parentheses are SSIM for input data.
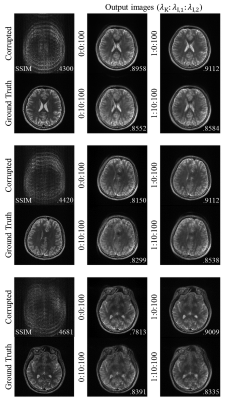
Figure 3. Motion corrected images from
the proposed network on the synthesized test dataset. Input corrupted images
and motion-free ground-truth images are given on the first column. Motion
corrected images with the different loss weights are given with SSIM of all
result images.
DOI: https://doi.org/10.58530/2022/0963