0958
Low Rank Off-resonance Correction for Double Half-Echo k-Space Acquisitions1UCLA, Los Angeles, CA, United States
Synopsis
The present study describes a model-based approach for correcting off-resonance in the context of short echo-time imaging using a double half-echo k-space acquisition. This technique employs center-out readouts in forward and reverse directions and is sensitive to off-resonance. The correction is simple and results in a marked reduction in blurring for a negligble cost in pre-processing.
Introduction
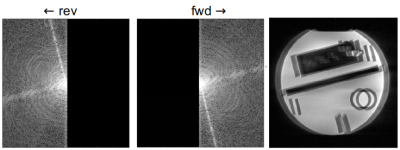
Fractional sampling along the readout direction is a well-known strategy for reducing echo times (TE). The lower limit of 50% (aka half echoes) can be attained by acquiring two readouts with the gradient polarity reversed, as depicted in Figure 1.1 While individual half echoes cannot be reconstructed, the paired acquisition effectively provides a full line of k-space with the TE of a half echo.Field inhomogeneity (B0) induces a phase modulation along the frequency encode direction that results in image pixel shifts in opposite directions for fwd and rev. This blurring effect can be observed in the combined half kspaces in Figure 1. Low rank reconstruction2-4 may be used to reconstruct fwd and rev in the presence of gradient delays5 but cannot accomodate B0, which is not modeled as a shift-invariant convolution. Therefore another correction is needed.
One approach is to segment the data in time, so that the phase can be approximated as constant inside a segment with discrete changes occurring between segments, which is amenable to low rank modeling.6 This general approach is applicable to EPI acquisitions that are especially sensitive to B0. However half echo acquisitions are relatively simple and do not require the same treatment; the present abstract describes a low-order analytical model of B0 to correct fwd/rev pixel shifts.
Methods
The lowest order B0 correction is a constant term, which is the source of pixel shifts between fwd and rev, as represented by the following equations:- $$$fwd(k) = kspace(k) . exp(+iΔf.k)$$$
- $$$rev(k) = kspace(k) . exp(-iΔf.k)$$$
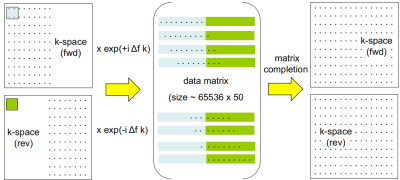
If fwd and rev can be reconstructed separately into images then the correction parameter can be found by optimizing a similarity metric, e.g. the squared difference, as used in tools for unwarping EPI distortions.7 For half echoes, however, reconstruction is only possible from the paired acquisition. Trial corrections can be made to optimize a quality metric such as entropy8; in the context of low rank reconstruction an interesting metric is the nuclear norm of the data matrix (see Figure 2).
Numerical explorations indicated that entropy and nuclear norm are both robust predictors of Δf. The nuclear norm has the advantage that it can return an accurate result from the incomplete matrix (containing missing samples), which makes it possible to correct Δf quickly prior to reconstruction by the (slow) matrix completion step.
Experimental
Data were acquired on a 3T system (Siemens Prisma Fit) using a dual tuned Na/H transmit/receive head coil (RAPID Biomedical). A 3D Cartesian spoiled gradient echo, double half echo sequence tuned to sodium was used: TE 1.0 ms (echo fraction 0.5), TR 9 ms, flip angle 35 degrees, 0.64 ms RF pulse (asymmetric windowed sinc), readout bandwidth 80 Hz/pixel, matrix 50x50x64, voxel size 5x5x5 mm, 10 averages, scan time 10 minutes. A healthy adult was recruited as part of an IRB approved study giving written informed consent. Reconstructions were performed in Matlab 2020b on a Nvidia RTX4000 GPU using the method described in Ref 2. A 5x5 kernel was used and iterations were terminated when the relative change was less than 10-7. Nonlinear optimization over Δf was performed using fminunc() or fminsearch() in the case of entropy where derivatives were unreliable.Results
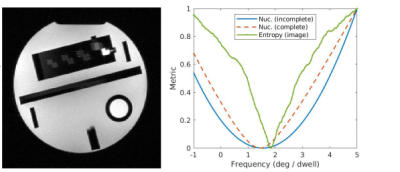
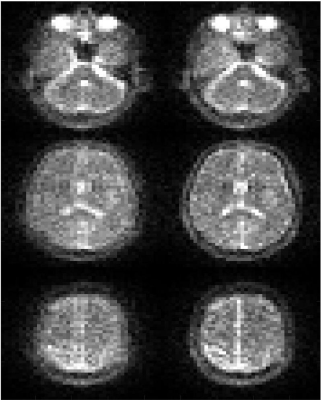
Phantom 1H results in Figure 3 show the correction of B0 using the image entropy or the nuclear norm of data matrix as metrics. Both have minima close to the applied off-resonance of 400 Hz (corresponding to 1.87 degrees / dwelltime), confirming the validity of the correction method. In vivo 23Na results are presented in Figure 4. Three slice locations are shown with no off-resonance correction (left column) and with the proposed off-resonance correction (right column). Similar to the phantoms, there is a clear reduction in blurring in the latter case.Discussion
The present study has developed a low order model-based correction for off-resonance of forward and reverse half echoes. The correction is fast and robust to noise and missing samples. In application to sodium imaging, half echoes are employed to reduce the TE while maintaining a low bandwidth to gain SNR. This makes the acquisitions sensitive to off-resonance, necessitating B0 correction.Correcting for a constant off-resonance term reduces blurring and can also be important to remove misregistration errors in dual modality and interventional radiotherapy systems. Generalization to a linear term in the frequency direction could reduce stretching/shrinking of the object, but this was not found to be a significant source of artefact in the present study.
In conclusion, low-order modeling of B0 is useful to correct blurring and misregistration pixel shifts in sequences employing 2 or more readout directions.
Acknowledgements
No acknowledgement found.References
1. Scheidegger MB, Maier SE, Boesiger P. FID-Acquired-Echos: A short echo time imaging method for flow artefact suppression. Magn Reson Imaging 1991; 9(4): 517-524
2. Shin PJ, Larson PE, Ohliger MA, et al. Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion. Magn Reson Med. 2014; 72(4):959-970
3. Lee D, Jin KH, Kim EY, Park SH, Ye JC. Acceleration of MR parameter mapping using annihilating filter-based low rank hankel matrix. Magn Reson Med 2016; 76: 1848
4. Haldar JP. Low-rank modeling of local k-space neighborhoods for constrained MRI. IEEE Trans Med Imaging. 2014; 33(3):668-681
5. Bydder M, Ali F, Ghodrati V, Hu P, Yao J, Ellingson BM. Minimizing echo and repetition times in magnetic resonance imaging using a double half-echo k-space acquisition and low-rank reconstruction. NMR Biomed. 2021;34(4):e4458
6. Balachandrasekaran A, Mani M, Jacob M. Calibration-Free B0 Correction of EPI Data Using Structured Low Rank Matrix Recovery. IEEE Trans Med Imaging. 2019;38(4):979-990
7. Andersson JL, Skare S, Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. Neuroimage. 2003; 20(2): 870-88
8. Atkinson D, Hill D L G, Stoyle P N R, Summers P E and Keevil S F. Automatic Correction of Motion Artefacts in Magnetic Resonance Images Using an Entropy Focus Criterion. IEEE Trans Med Imaging 1997; 16(6): 903-910
Figures