0956
Gibbs-ringing Removal through Anti-aliased Deep Priors
Jaeuk Yi1, Chuanjiang Cui1, Kyu-Jin Jung1, and Dong-Hyun Kim1
1Department of Electrical and Electronic Engineering, Yonsei University, Seoul, Korea, Republic of
1Department of Electrical and Electronic Engineering, Yonsei University, Seoul, Korea, Republic of
Synopsis
Inspired by recent usage of Deep Image Prior (DIP) in the field of MRI that utilizes a powerful low-level image prior from a neural network architecture itself without any training dataset, we conduct k-space extrapolation using the deep prior for Gibbs-ringing removal in order to build general Gibbs-ringing correction algorithm without dependency on the dataset. We further improved the existing deep prior with the addition of anti-aliasing layers. The proposed deep prior method outperformed conventional non-learning methods quantitively and qualitatively in numerical simulations and in-vivo data.
Introduction
Deep Image Prior (DIP)1 demonstrated that a convolutional neural network (CNN) architecture itself can work as a powerful low-level image prior without any training dataset showing impressive results for denoising, inpainting, etc. Recently, it has been applied to the field of MRI such as dynamic MRI2, compressed sensing3, and parallel imaging4.Although recent deep learning-based methods5,6 have achieved state-of-the-art performance in Gibbs-ringing removal, their generalizability out of training dataset is still questionable. In contrast, the DIP method is a non-learning model-based optimization but uses CNN architecture instead of existing explicit priors such as sparsity.
In this study, we investigate the usage of the deep priors on k-space extrapolation for Gibbs-ringing removal. We also conduct a comparative study between the proposed method and conventional ringing removal methods.
Methods
[Algorithm]The objective for k-space extrapolation is to recover untruncated k-space of the high-resolution (HR) image $$$x$$$ from given truncated k-space measurement $$$y$$$ of the low-resolution (LR) image, which is given by
$$\hat{x}=\underset{x}{\arg\min} \left\lVert \tilde{\mathcal{F}}x-y \right\rVert ^{2}$$
where $$$\tilde{\mathcal{F}}$$$ is truncated Fourier transform which removes the high k-space region of $$$\left\lvert k \right\rvert \geq \left\lvert k_c \right\rvert$$$ for some known $$$k_c$$$7. This optimization problem is ill-posed as there are an infinite number of solutions $$$\hat{x}$$$ for a single measurement $$$y$$$. DIP replaces $$$x$$$ with the network output $$$f(z;\theta)$$$ to improve the search space of the solution $$$\hat{x}$$$ by exploiting low-level image priors of the architecture itself as depicted in Fig.1b.
$$\hat{\theta}=\underset{\theta}{\arg\min} \left\lVert \tilde{\mathcal{F}}f(z;\theta)-y \right\rVert ^{2}$$
$$\hat{x}=f(z;\hat{\theta})$$
where $$$z$$$ is a fixed random input, and $$$\theta$$$ is randomly initialized network parameters as shown in Fig.1a. Training dataset is not required for this process.
After optimization, we replace the low k-space region of the solution $$$\hat{x}$$$ with the acquired measurement $$$y$$$ to maintain consistency with the acquired data4.
[Network Design]
The network follows the structure of Deep Decoder (DD), a simple decoder-only non-convolutional architecture whose architectural prior performs on par with DIP in various tasks8. Our modification is the addition of blur pooling layers9 to enforce smoother prior without increasing the number of parameters such as the number of channels or layers4 as shown in Fig.2a. Blur pooling mitigates aliasing in the form of checkerboard artifacts due to the upsampling operation9-11. Although bilinear upsampling itself can be interpreted as applying a 1-2-1 blur filter after upsampling9, we found that its amount of blur is not sufficient to remove checkerboard artifacts in the initial output as shown in Fig.2a.
[Evaluation]
1. Numerical simulation: All Gibbs-ringing artifacts are simulated by cropping center ⅓×⅓ of k-space of the ground truth image, except for the MR image in Fig.3a where center ¼×¼ of k-space is acquired. For evaluation on an MR dataset in Fig.4, we used center slices from 578 T2-weighted and 578 PD-weighted brain volumes from the IXI dataset. They are coil-combined magnitude-only 256x256 images. Various conventional non-learning methods for Gibbs-ringing removal including widely used local subvoxel shift12 were used for comparison. Note that PSNR/SSIM values are only calculated for HR methods as these metrics require the output to have the same resolution as the ground truth image.
2. In-vivo acquisition: In-vivo data from one subject were acquired on a 3T Siemens Prisma using a 2D multi-slice spin-echo sequence with the following protocol: TR/TE=2000/20ms, in-plane resolution=2.0mm2, slice thickness=3.0mm, matrix size=128×128.
For all experiments, the network consisted of 5 layer blocks where each block has 128 channels, which was the default setting of DD8. For all optimization-based methods, we employed Adam optimizer13 with a learning rate of 0.01, and the learning rate was decayed to 0.0001 exponentially over a total of 5000 iterations.
Results
Fig.3 presents evaluation on some example images from various domains. In Fig.3a and Fig.3b, the proposed deep prior method removes Gibbs-ringing while preserving edges achieving the highest SSIM among the HR methods except for the phantom image where total variation performs better than deep prior. Our method shows finer and less pixelated structures than the local subvoxel shift method12 which should be directly applied to low-resolution images14.Fig.4 and Fig.5 present evaluation on the large MR dataset and in-vivo data respectively. The proposed deep prior method shows superior performance to other conventional methods both quantitatively (Fig.4a) and qualitatively (Fig.4b, Fig.5).
Fig.2 demonstrates the effectiveness of using blur pooling layers for Gibbs-ringing removal. Blur pooling enforces smoother initial $$$f(z;\theta)$$$ by removing checkerboard artifacts due to upsampling operation. This results in less residual ringing but still does not incur blurred edges achieving higher performance than one without blur pooling.
Discussion and Conclusion
We proposed a new Gibbs-ringing removal algorithm using deep priors and showed its superior performance to conventional methods. Also, our method is quite generalizable; we did not tune any hyperparameters per image or dataset for all conducted experiments. But further performance improvements might be possible by tuning the hyperparameters.Besides, we found that full recovery of high-frequency details of the original ground truth image was not possible (Fig.3~5) using only low-level prior as the Gibbs model acquires 0% of the high k-space region above truncation.
Acknowledgements
NoneReferences
1. D. Ulyanov, A. Vedaldi, and V. Lempitsky, “Deep image prior,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2018, pp. 9446–9454.2. J. Yoo, K. H. Jin, H. Gupta, J. Yerly, M. Stuber, and M. Unser, “Time-Dependent Deep Image Prior for Dynamic MRI,” IEEE Trans. Med. Imaging, 2021.
3. D. Van Veen, A. Jalal, M. Soltanolkotabi, E. Price, S. Vishwanath, and A. G. Dimakis, “Compressed sensing with deep image prior and learned regularization,” ArXiv Prepr. ArXiv180606438, 2018.
4. M. Z. Darestani and R. Heckel, “Accelerated MRI with un-trained neural networks,” IEEE Trans. Comput. Imaging, vol. 7, pp. 724–733, 2021.
5. M. J. Muckley et al., “Training a neural network for Gibbs and noise removal in diffusion MRI,” Magn. Reson. Med., vol. 85, no. 1, pp. 413–428, 2021.
6. Q. Zhang et al., “MRI Gibbs-ringing artifact reduction by means of machine learning using convolutional neural networks,” Magn. Reson. Med., vol. 82, no. 6, pp. 2133–2145, 2019.
7. J. Veraart, E. Fieremans, I. O. Jelescu, F. Knoll, and D. S. Novikov, “Gibbs ringing in diffusion MRI,” Magn. Reson. Med., vol. 76, no. 1, pp. 301–314, 2016.
8. R. Heckel and P. Hand, “Deep decoder: Concise image representations from untrained non-convolutional networks,” ArXiv Prepr. ArXiv181003982, 2018.
9. R. Zhang, “Making convolutional networks shift-invariant again,” in International conference on machine learning, 2019, pp. 7324–7334.
10. A. Odena, V. Dumoulin, and C. Olah, “Deconvolution and checkerboard artifacts,” Distill, vol. 1, no. 10, p. e3, 2016.
11. T. Karras, S. Laine, and T. Aila, “A style-based generator architecture for generative adversarial networks,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019, pp. 4401–4410.
12. E. Kellner, B. Dhital, V. G. Kiselev, and M. Reisert, “Gibbs-ringing artifact removal based on local subvoxel-shifts,” Magn. Reson. Med., vol. 76, no. 5, pp. 1574–1581, 2016.
13. D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” ArXiv Prepr. ArXiv14126980, 2014.
14. K. Zhao, Z. Xu, F. Huang, Y. Mei, and Y. Feng, “Interlaced Total Variation for Gibbs Artifact Reduction in the Presence of Zero Padding,” ISMRM, 2018.
Figures
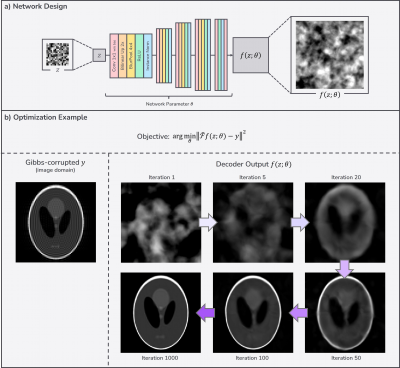
Figure 1. Overall algorithm. a) Network design. It is the Deep Decoder8 architecture with the addition of blur pooling layers9. b) Gibbs-removal example for the phantom image. The output of the architecture tends to be smooth while preserving edges.
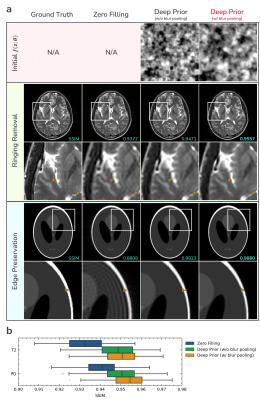
Figure 2. Effectiveness of blur pooling for Gibbs-ringing removal. Exactly same random initialization is used for network input and parameters; The only difference is the existence of blur pooling layers. a) Usage of blur pooling further removes ringing artifacts while it does not incur blurring at edges. b) Performance evaluation on the same IXI dataset as in Fig.4. Higher performance has been achieved when using blur pooling.
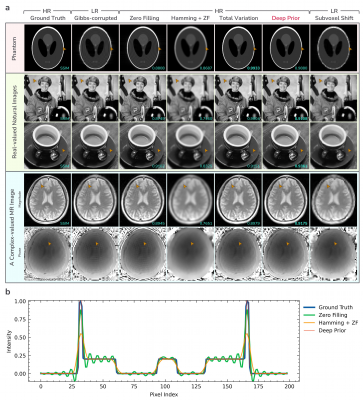
Figure 3. a) Numerical simulations of Gibbs-ringing artifacts on images from various domains. b) Intensity profile of the center horizontal line of the phantom image. For deep prior, we do not tune any hyperparameters per image; the same hyperparameters are used for all images. Deep prior removes Gibbs-ringing while preserving edges recovers the original resolution of the ground truth.
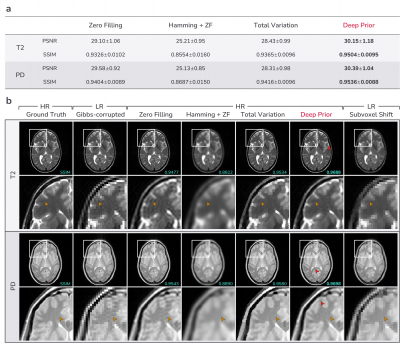
Figure 4. Evaluation on numerical simulations of Gibbs-ringing artifacts on T2-weighted and PD-weighted images from IXI dataset. a) Performance evaluation of HR methods which results in the same resolution as the ground truth. b) Visual comparison. Red arrows indicate residual ringing artifacts remained in the deep prior method.
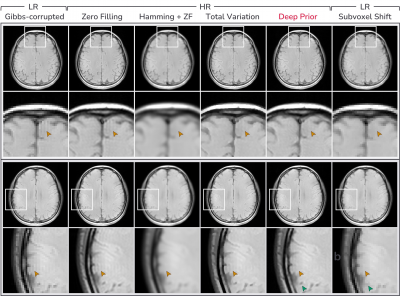
Figure 5. Evaluation on in-vivo Gibbs-ringing artifacts. For HR methods, we assume that the ground truth has three times higher resolution than the Gibbs-ringed image. Deep prior mitigates Gibbs-ringing artifacts and shows finer structures (green arrows) than the local subvoxel shift method12.
DOI: https://doi.org/10.58530/2022/0956