0951
Assessment of Instabilities of Conventional and Deep Learning Multi-Coil MRI Reconstruction at Multiple Acceleration Factors1Center for Biomedical Imaging, Department of Radiology, NYU School of Medicine, New York, NY, United States, 2Center for Advanced Imaging Innovation and Research (CAI2R), NYU School of Medicine, New York, NY, United States, 3Department Artificial Intelligence in Biomedical Engineering, FAU Erlangen-Nuremberg, Erlangen, Germany
Synopsis
Although deep learning has received much attention for accelerated MRI reconstruction, it shows instabilities to certain tiny perturbations resulting in substantial artifacts. There has been limited work comparing the stability of DL reconstruction with conventional reconstruction methods such as parallel imaging and compressed sensing. In this work, we investigate the instabilities of conventional methods and the Variational Network (VN) with different accelerations. Our results suggest that CG-SENSE with an optional regularization is also impacted by perturbations but shows less artifacts than the VN. Each reconstruction method becomes more vulnerable with higher acceleration and VN shows severe artifacts with 8-fold acceleration.
Introduction
Deep learning (DL) reconstruction1-3 is a promising method for accelerating MRI, due to its improved image quality. One such method is the Variational Network (VN), which demonstrated successful reconstruction of 4-fold accelerated knee images2. However, it is acknowledged that neural network show instabilities on tiny perturbations4,5, which results in substantial artifacts for MRI reconstruction6,7. To our knowledge, there is no similar exploration on the instabilities of conventional reconstruction methods, such as parallel imaging8,9 and compressed sensing10. Further, no studies have discussed how the instabilities change with different accelerations. It is an open question if the vulnerability to perturbations increases as the reconstruction model gets more complex.In this work, we investigate how tiny worse-case perturbations affect the performance of conventional conjugate-gradient (CG)-SENSE with L2 and nonlinear total variation regularization11 and DL-based VN with different accelerations. Our results indicate that conventional reconstruction methods were also impacted by the perturbation but show less artifacts than VN, and each reconstruction method becomes more vulnerable to the perturbation with higher acceleration factor.Methods
MRI reconstruction Algorithm: The problem of multi-coil MRI reconstruction can be formulated as:$$\min_{x} \parallel{y-Ex}\parallel_2^2 + R(x)$$
where $$$y$$$ is the undersampled k-space data, $$$x$$$ is the image, and $$$E$$$ is the encoding operator. $$$R()$$$ is an additional regularizer, e.g. Tikhonov12 or total variation (TV)11. CG-SENSE8,13 aims to solve this inverse problem without regularization. A fixed number of CG-iterations (N = 30) was used in all numerical experiments in this work.
As an example of DL-based method, the variational network with a Unet14 regularizer was used. The VN was implemented in PyTorch with the Adam optimizer15. Optimization is performed for 50 epochs, with a learning rate of 10-3. Knee images acquired with 15-channel coils from the fastMRI dataset16 were used to train the network with R = 4, 6 and 8 acceleration, respectively. The training data consisted of 668 2D slices from 26 patients. Sensitivity maps were obtained by ESPIRiT17. A uniform undersampling mask with 24 center calibration lines was applied.
Tiny Worse-Case Perturbation: The tiny perturbation was modeled as follows: Given an image and a reconstruction method, the algorithm aims to find a perturbation in the image domain that maximizes the change of the reconstruction image while keeping the perturbation small. It can be described mathematically as follows:
$$\max_{r} \parallel{f(y+Er)-f(y)}\parallel_2^2 - \lambda\parallel{r}\parallel_2^2$$
where $$$r$$$ is the perturbation in image domain, and $$$f$$$ models the given reconstruction method (conventional or deep learning reconstruction). $$$\lambda$$$ is the weighting parameter on the l2-norm of the perturbation, which was chosen empirically. Gradient ascent with momentum was used to find the optimal solution of $$$r$$$6,18. Optimized perturbations were obtained individually for each tested reconstruction model and each acceleration factor.
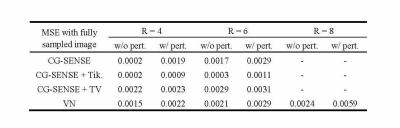
Testing Experiments: Coronal knee MRI data with 15-channel coils from the fastMRI dataset were used for testing the instabilities. Uniform undersampling masks with acceleration factors R = 4, 6 and 8 and 24 autocalibration lines at the center of k-space were used for each reconstruction method. The reconstruction results were evaluated quantitatively in terms of mean square error (MSE) to the ground truth reconstructed with fully sampled data.
Results
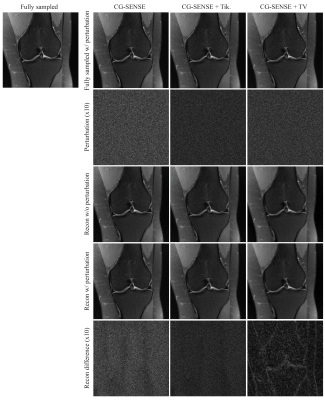
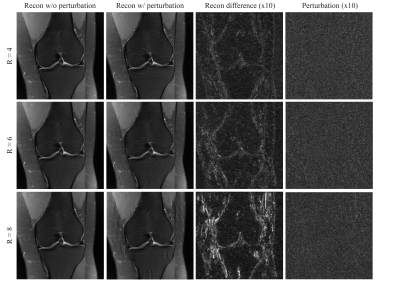
The reconstruction results for conventional methods, including CG-SENSE, CG-SENSE with Tikhonov or TV regularization are shown Figure 1. The perturbation is barely visible to the human eye. In the case of R = 4 acceleration, the worst-case perturbation leads to subtle differences in the reconstructed images, with different characteristics for the different reconstruction methods. CG-SENSE with TV shows larger differences on the edges of the knee.The perturbations and reconstruction results with and without perturbation of the VN method with R = 4, 6 and 8 accelerations are shown in Figure 2. The severity of the differences and artifacts increases as the acceleration factor is increased and larger differences occur on the edges of the knee. The most severe artifacts can be observed for the VN at high acceleration (R = 8).Table 1 summarized the MSE of the reconstruction results (with or without perturbation) to the fully sampled ground truth image. It is observed that for each method, a much larger difference was found in VN at R = 8 acceleration. Under the same acceleration factor, CG-SENSE with TV shows the largest difference and CG-SENSE with Tikhonov shows the smallest difference.Discussion and Conclusions
The performed instability analysis shows the conventional methods were also impacted by the certain tiny worst-case perturbation but show less artifacts than VN reconstructions. Our findings suggest that the linear data consistency was more stable to the perturbation than the non-linear regularization. CG-SENSE with Tikhonov regularization shows the highest robustness to adversarial perturbations.Different reconstruction methods yield different artifacts. The perturbations optimized by the same algorithm are different for each reconstruction method, which implies that the tiny-worse case perturbation is very specific for each method. CG-SENSE with TV and VN shows a similar pattern of the reconstruction differences, which might be caused by the total variation constraint and be more vulnerable to the perturbation.It is observed that each method becomes more vulnerable to the perturbation with increasing acceleration factor because the inverse problem is ill-conditioned at higher acceleration factors.Acknowledgements
No acknowledgement found.References
1. McCann MT, Jin KH, Unser M. Convolutional Neural Networks for Inverse Problems in Imaging: A Review. IEEE Signal Processing Magazine 2017;34:85–95.
2. Hammernik K, Klatzer T, Kobler E, et al. Learning a variational network for reconstruction of accelerated MRI data: Learning a Variational Network for Reconstruction of Accelerated MRI Data. Magn. Reson. Med 2018;79:3055–3071.
3. Knoll F, Hammernik K, Zhang C, et al. Deep-Learning Methods for Parallel Magnetic Resonance Imaging Reconstruction. IEEE Signal Processing Magazine 2020;37:128–140.
4. Moosavi-Dezfooli S-M, Fawzi A, Fawzi O, Frossard P. Universal Adversarial Perturbations. In: Honolulu, HI: IEEE; 2017. pp. 86–94.
5. Fawzi A, Seyed-Mohsen M-D, Pascal F. The robustness of deep networks – A geometric perspective. IEEE Signal Processing Magazine 2017;34:50–62.
6. Antun V, Renna F, Poon C, Adcock B, Hansen AC. On instabilities of deep learning in image reconstruction and the potential costs of AI. Proc Natl Acad Sci USA 2020;117:30088–30095.
7. Calivá F, Cheng K, Shah R, Pedoia V. Adversarial Robust Training of Deep Learning MRI Reconstruction Models. arXiv:2011.00070 [cs, eess] 2021.
8. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magnetic Resonance in Medicine 1999;42:952–962.
9. Griswold MA, Jakob PM, Heidemann RM, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn. Reson. Med. 2002;47:1202–1210.
10. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007;58:1182–1195.
11. Block KT, Uecker M, Frahm J. Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint. Magn. Reson. Med. 2007;57:1086–1098.
12. Tikhonov AN, Arsenin VI. Solutions of ill-posed problems. New York 1977;1:30.
13. Pruessmann KP, Weiger M, Börnert P, Boesiger P. Advances in sensitivity encoding with arbitrary k -space trajectories. Magn. Reson. Med. 2001;46:638–651.
14. Ronneberger O, Fischer P, Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In: Navab N, Hornegger J, Wells WM, Frangi AF, editors. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015. Vol. 9351. Lecture Notes in Computer Science. Cham: Springer International Publishing; 2015. pp. 234–241.
15. Kingma DP, Ba J. Adam: A Method for Stochastic Optimization. arXiv:1412.6980 [cs] 2017.
16. Knoll F, Zbontar J, Sriram A, et al. fastMRI: A Publicly Available Raw k-Space and DICOM Dataset of Knee Images for Accelerated MR Image Reconstruction Using Machine Learning. Radiology: Artificial Intelligence 2020;2:e190007.
17. Uecker M, Lai P, Murphy MJ, et al. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn. Reson. Med. 2014;71:990–1001.
18. Qian N. On the momentum term in gradient descent learning algorithms. Neural Networks 1999;12:145–151.
Figures