0947

Coil-sketched unrolled networks for computationally-efficient deep MRI reconstruction
Julio A Oscanoa1, Batu Ozturkler2, Siddharth S Iyer3,4, Zhitao Li2,4, Christopher M Sandino2, Mert Pilanci2, Daniel B Ennis4, and Shreyas S Vasanawala4
1Department of Bioengineering, Stanford University, Stanford, CA, United States, 2Department of Electrical Engineering, Stanford University, Stanford, CA, United States, 3Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Boston, MA, United States, 4Department of Radiology, Stanford University, Stanford, CA, United States

Synopsis

Deep unrolled networks can outperform conventional compressed sensing reconstruction. However, training unrolled networks has intensive memory and computational requirements, and is limited by GPU-memory constraints. We propose to use our previously developed “coil-sketching” algorithm to lower the computational burden of the data consistency step. Our method reduced memory usage and training time by 18% and 15% respectively with virtually no penalty on reconstruction accuracy when compared to a state-of-the-art unrolled network.

Introduction

Deep learning (DL) reconstruction frameworks using unrolled network architectures that alternate between denoising and data-consistency have proven to outperform conventional compressed sensing by yielding more accurate and faster reconstructions [1-4]. However, this comes with excessive computational cost, especially for training CNN-based architectures, as large arrays need to be stored in memory to perform back-propagation. This issue hinders their application to higher dimensional datasets such as dynamic or 3D non-cartesian MRI.

We recently developed a general method for computationally-efficient image reconstruction termed “coil sketching” [5]. Coil sketching reduces the computational cost by reducing the number of coils actively used during the data consistency step via a randomized sketching approach [6,7]. Here, we present a proof-of-concept that applies coil sketching to deep unrolled networks. Our method lowers the computational cost and memory footprint of training with virtually no penalty on reconstruction accuracy as shown in 2D knee datasets.

Theory

Image reconstruction with DL regularization.
We focus on the following MR reconstruction problem from the MOdel-based reconstruction using Deep Learned priors (MoDL) formulation:

$$x^* = \underset{x}{\text{argmin}} \underbrace{\frac{1}{2}\lVert Ax - y \rVert_2^2}_{\text{Data consistency (DC)}} + \underbrace{\lambda \lVert x - \mathcal{D}_W(x)\rVert_2^2}_{\text{DL regularization}} \;\text{ [Eq. 1]}$$

where $$$x$$$ is the image, $$$y$$$ is the acquired kspace, $$$A=UFC$$$ with $$$U$$$ being the undersampling mask, $$$F$$$ being the fourier transform, and $$$C$$$ being the coil sensitivity maps, and $$$\mathcal{D}$$$ is a learned CNN denoiser parameterized by $$$W$$$.

Coil sketching reconstruction
In coil sketching, instead of solving Eq. 1 directly, we break the problem into multiple lower-dimension subproblems which we solve sequentially. Each subproblem has a sketched DC term that represents a second-order Taylor approximation around the current estimate $$$x^t$$$ with a sketched Hessian $$${A^t_S}^H A^t_S$$$:
$$ x^{t+1} = \text{arg}\min_x \underbrace{\frac{1}{2} \left \| A^t_S (x - x^t) \right \|^2_2 + \langle x,A^H(Ax^t - y) \rangle}_{\text{Sketched data consistency}} + \underbrace{\lambda \lVert x - \mathcal{D}_W(x)\rVert_2^2}_{\text{DL regularization}} \; \text{ [Eq. 2]}$$
where $$$A^t_S = S^t A = U F C^t_S$$$ is a lower-dimensional forward model produced by a random projection of the matrix in the coil dimension, which effectively reduces the number of coils actively used during reconstruction. Since this formulation only changes the DC term, Eq. 2 can be solved using the same optimizer for any regularization, including DL-based.

Methods

Sketching unrolled networks
Figure 1a shows the unrolled network reconstruction framework, where we alternate between CNN-denoising and DC steps. While the original MoDL framework applied DC using the forward model $$$A$$$ (Fig. 1b), the sketched MoDL framework applies DC using multiple randomly-generated lower-dimensional models $$$A^t_S$$$, lowering computational complexity and speeding up the process [5].

Algorithm
The original MoDL framework solves Eq. 1 applying half-quadratic splitting [1], which yields the algorithm in Fig. 2a. The DC step consists of solving the linear system in Eq. 3 using Conjugate Gradient. Our proposed sketched MoDL framework only changes the DC step by solving multiple linear systems (Eq. 4-5) using the conjugate gradient method.

Evaluation
We considered three networks:

  • Baseline-MoDL, which accords with the original MoDL framework (Fig. 2a)
  • Plug-n-play sketched MoDL (PnP-MoDL), which uses the trained baseline MoDL network weights, then replaces the DC steps at inference (Fig. 1b) with sketched DC steps (Fig. 1c). The aim is to test equivalency of both original and sketched DC steps.
  • Sketched-MoDL, which uses the MoDL framework with sketched DC steps for training and inference(Fig. 2b)

The dataset and training details are in Table 1. For the sketched networks, the number of coils was reduced from 8 to 4 using a randomly-generated gaussian sketching matrix [7]. To evaluate training, we compared memory usage and iteration time between Baseline-MoDL and Sketched-MoDL. For inference, we compared memory usage, reconstruction time, and image metrics (NRMSE, SSIM and PSNR) for the three networks.

Results

Figure 3 shows a visual comparison between reconstruction with the three networks. The three networks have virtually equal performance. Table 2 shows the summary of the metrics measured. For training, Sketched-MoDL has -18% memory usage and -15% time per iteration. For inference, the three networks have marginally different image metrics; whereas both sketched MoDL networks have faster reconstruction times but higher memory usage during inference.

Discussion

For training, Sketched-MoDL shows a promising decrease in memory usage that could facilitate DL-based reconstruction of higher dimensional datasets, especially for non-cartesian 3D, where efficient coil compression techniques like GCC [8] cannot be used. Additionally, the decrease in iteration time could reduce the total training time by days, since networks are typically trained for tens of thousands of iterations. Additionally, our method can be flexibly integrated into various unrolled methods as a substitute for data-consistency, in contrast to other memory-efficient techniques such as [9] that require invertible layers. Regarding inference, the three networks present virtually the same image metrics, which indicates no penalty on reconstruction accuracy.

Conclusion and Future Work

We have demonstrated a proof-of-concept that applies coil sketching to a standard deep unrolled network architecture for MR image reconstruction. Our method reduces training memory usage with virtually no penalty on reconstruction accuracy. This reduced computational cost could be leveraged to facilitate DL-based reconstruction of higher dimensional datasets such as dynamic imaging or 3D non-cartesian. Future work includes translating computational memory and performance gains at inference time, sketching distribution optimization, and general hyper-parameter optimization.

Acknowledgements

This project was supported by NIH R01 EB026136 and NIH R01 EB009690.

References

  1. Aggarwal, H. K., Mani, M. P., & Jacob, M. (2018). MoDL: Model-based deep learning architecture for inverse problems. IEEE transactions on medical imaging, 38(2), 394-405.
  2. Hammernik, K., Klatzer, T., Kobler, E., Recht, M. P., Sodickson, D. K., Pock, T., & Knoll, F. (2018). Learning a variational network for reconstruction of accelerated MRI data. Magnetic resonance in medicine, 79(6), 3055-3071
  3. Sandino, C. M., Cheng, J. Y., Chen, F., Mardani, M., Pauly, J. M., & Vasanawala, S. S. (2020). Compressed sensing: From research to clinical practice with deep neural networks: Shortening scan times for magnetic resonance imaging. IEEE signal processing magazine, 37(1), 117-127.
  4. Yang, Y., Sun, J., Li, H., & Xu, Z. (2018). ADMM-CSNet: A deep learning approach for image compressive sensing. IEEE transactions on pattern analysis and machine intelligence, 42(3), 521-538.
  5. Oscanoa, J. A., Ong, F., Li, Z., Sandino, C. M., Ennis, D. B., Pilanci, M., & Vasanawala, S. S. Coil Sketching for fast and memory-efficient iterative reconstruction. ISMRM 28th Annual Meeting, May 15-20th 2021 (Virtual meeting).
  6. Pilanci, M., & Wainwright, M. J. (2016). Iterative Hessian sketch: Fast and accurate solution approximation for constrained least-squares. The Journal of Machine Learning Research, 17(1), 1842-1879
  7. Pilanci, M., & Wainwright, M. J. (2015). Randomized sketches of convex programs with sharp guarantees. IEEE Transactions on Information Theory, 61(9), 5096-5115
  8. Zhang, T., Pauly, J. M., Vasanawala, S. S., & Lustig, M. (2013). Coil compression for accelerated imaging with Cartesian sampling. Magnetic resonance in medicine, 69(2), 571-582.
  9. Kellman, M., Zhang, K., Markley, E., Tamir, J., Bostan, E., Lustig, M., & Waller, L. (2020). Memory-efficient learning for large-scale computational imaging. IEEE Transactions on Computational Imaging, 6, 1403-1414.

Figures

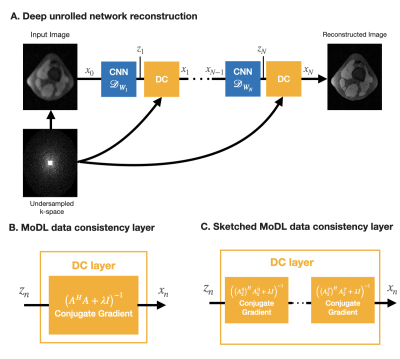
Figure 1. Diagram of coil-sketched unrolled networks. (A) General deep unrolled network architecture that alternates between CNN-denoising and data-consistency (DC) steps. (B) In MoDL, the DC layer solves a linear system with the MRI forward model A. (C) In Sketched-MoDL, we change the DC layer to solve instead multiple smaller subproblems using randomly-generated lower-dimensional models $$$A^t_S$$$.

Figure 2. MoDL vs. Sketched-MoDL algorithms.

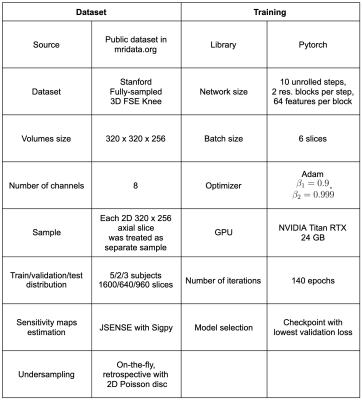
Table 1. Dataset and training details

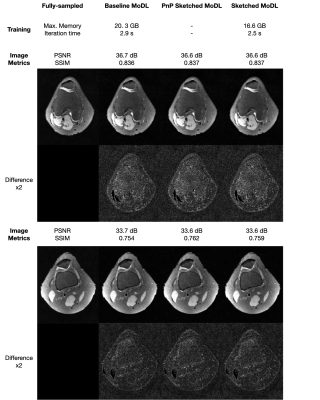
Figure 3. Visual assessment. We present inference results for two slices from the test dataset reconstructed with baseline MoDL, PnP sketched MoDL, and sketched MoDL. Both visually and through image metrics, the results are marginally different.

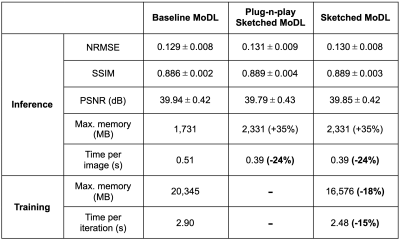
Table 2. Metrics comparison for inference on the test dataset and training. Image metrics show virtually equal performance between the three networks. However, Sketched MoDL has lower memory usage (-18%) and reduced iteration time (-15%) during training

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)
0947
DOI: https://doi.org/10.58530/2022/0947