0879
Testing the feasibility and effectiveness of bundle-based global tractography (bundle-o-graphy) in real human brain data1University of Verona, Verona, Italy, 2University of Sherbrooke, Sherbrooke, QC, Canada, 3Department of Neuroscience, Rehabilitation, Ophthalmology, Genetics, Maternal and Child Health (DINOGMI), University of Genoa, Genoa, Italy
Synopsis
We introduce a new formulation for bundle-based tractography global reconstruction (bundle-o-graphy). The idea is to move the focus from streamlines to bundle-based reconstruction thanks to a convenient reduction in the number of parameters needed to be optimized and the injection of anatomical priors. We show the potential of our approach on both synthetic and real data.
Introduction
Microstructure Informed Tractography1 approaches have shown the potential of exploiting tissue microstructure properties to improve the anatomical accuracy of the reconstructions. These methods can be divided into two classes based on the strategy they use to reconstruct the white matter (WM) pathways. The first implies the minimization of a global cost function that drives the tracking process and the signal reconstruction at the same time, while the second attempts to identify the optimal subset of streamlines from an initial set of candidates which are most compatible with the measured DW-MRI data. Both approaches are limited, the former by the high computational burden associated with the number of parameters needed to be optimized, the latter by the quality of the input candidates. We present a method to combine the strengths of both approaches by tackling tractography reconstruction from a different perspective. The idea is to move away from reconstructing individual streamlines and, instead, directly model groups of them (bundles), to reduce the parameters space extent. To this aim, we extended the Convex Optimization for Microstructure Informed Tractography (COMMIT2) to model groups of coherent streamlines using fewer parameters and to easily adapt their geometry and signal contribution using global optimization. In this work, we evaluated the effectiveness of bundle-o-graphy to improve connectivity estimates on both synthetic and real data.Methods
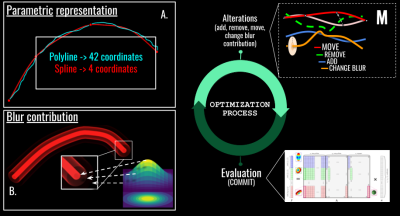
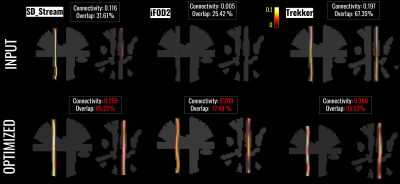
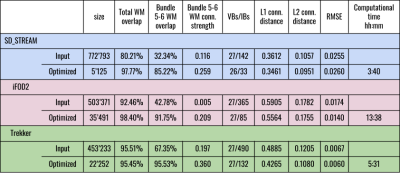
Given an input tractogram, we first employ Douglas-Peucker3 to reduce the number of points required to approximate the input trajectory (Fig 1A), which are then interpolated using cubic B-splines4. Each reduced streamline is then modeled as a cylinder of fixed radius extending along its trajectory mimicking the diffusion signal of a set of densely packed streamlines covering the whole volume of the cylinder. The spatial extent of the contribution corresponding to the streamlines in a bundle5 is modeled using a blur function with variable variance (Fig 1B). Thanks to this parameterization, bundle simulation turns into modeling the space of influence of a streamline, allowing the current streamline-based COMMIT to becoming a bundle-based algorithm. Different and more complex multivariate functions can be applied to optimize the shape of the bundle, as in 6, increasing the number of parameters needed to be optimized. The splines and the associated blur extent are optimized following an MCMC optimization with Metropolis-Hasting sampling scheme coupled with simulated annealing approach7.In this context, the coordinates of the control points, along with the variance of the blur function, represent the parameters of our model $$$M$$$ that need to be optimized. According to the Bayesian theory, we can infer the posterior distributions of these parameters based on the observed data d and the data generated by $$$M$$$. This, in turn, can be used to influence the parameters by back-propagation to minimize the cost function $$$f_T(M)$$$ defined as:$$f_T(M) = E_D (M,d) + λ|M|.$$The first term defines how well a specific configuration $$$M$$$ explains the observed data, while the second promotes the minimization of the number of bundles with the aim of reducing false-positive ones8. We assessed the effectiveness of bundle-o-graphy on the “ISBI 2013” dataset9 (64 directions at b-value=3000s/mm2, 1mm isotropic voxel, SNR=30) and tested three different tractography algorithms (iFOD210, SD_STREAM11, Trekker12 ) using default parameters. We evaluated white-matter coverage of the reconstructions, number of valid (VBs, true positives) and invalid bundles (IBs, false positives)13, as well as bundle specific and global connectivity estimations before and after bundle-o-graphy optimization. We also evaluate it on in-vivo human data from the “HCP test-retest” dataset14 (subject 172332) by generating 3M streamlines using SD_STREAM and default parameters.Results and Discussion
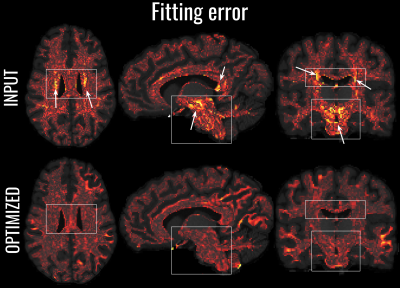
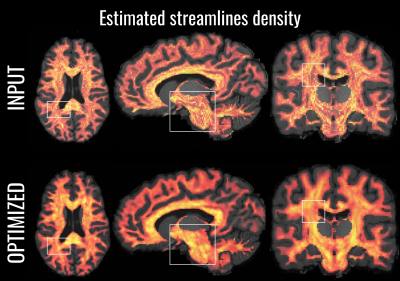
Results on synthetic data are summarized in Fig.2, which shows the impact of the optimization on the estimation of bundle specific and global connectivity estimates, WM coverage, error in connectivity strength estimation (L1- and L2-distance between estimated and GT connectivity matrices) and computational time required by bundle-o-graphy. The same setup was used across the experiments. Fig.3 visually inspects the intra-cellular signal fractions corresponding to a well-known hard-to-track-bundle, as reconstructed by different algorithms, before and after optimization with bundle-o-graphy. In-vivo data are shown in Fig.4 and Fig.5. In the former, the RMSE of the input (first row) and optimized (second row) tractograms are presented. Thanks to the bundle-based approach, we were able to dramatically reduce the number of parameters to optimize while, at the same time, improve the accuracy of modeling the underlying WM structure. Fig. 5, shows the comparison between the intra-cellular signal fractions maps of the tractogram before and after optimization with bundle-o-graphy. It’s worth noting how our method increases overall streamlines density homogeneity, improving white matter coverage on underrepresented regions.Conclusions
Bundle-o-graphy allows scaling-up tractography reconstructions moving from classic streamline-based optimization to bundles modeling. Bundle-o-graphy parameterization drastically reduces the parameters required to represent and optimize a set of streamlines, also allowing to inject additional prior knowledge to increase the accuracy and plausibility of the reconstructions. Our method proves the potentials and effectiveness of global reconstruction approaches, moving a step forward to their inclusion in clinical applications.Acknowledgements
No acknowledgement found.References
Daducci, A., Dal Palu, A., Descoteaux, M., Thiran, J.P.: Microstructure Informed Tractography: Pitfalls and Open Challenges. Front Neurosci 10(8), 247 (2016)
Daducci, A., Dal Palù, A., Lemkaddem, A., Thiran, J.P.: COMMIT: convex optimization modeling for microstructure informed tractography. IEEE Trans MedImaging 34(1), 246–57 (2015)
Duda, Richard O., Hart, Peter E.: “Pattern classification and scene analysis”. Wiley (1973)
Catmull, Edwin; Rom, Raphael: "A class of local interpolating splines". In Barnhill, Robert E.; Riesenfeld, Richard F. (eds.). Computer Aided Geometric Design. pp. 317–326 (1974)
Daducci, A., Gobbi, F., Febbrari, N., Battocchio, M., Schiavi, S., Proc. Intl. Soc. Mag. Reson. Med. 29, 4283(2021)
Close TG, Tournier JD, Johnston LA, Calamante F, Mareels I, Connelly A. Fourier Tract Sampling (FouTS): A framework for improved inference of white matter tracts from diffusion MRI by explicitly modelling tract volume. Neuroimage, 15;120:412-27 (2015)
Kirkpatrick S, Gelatt CD, Vecchi MP. Optimization by simulated annealing. 220:671–80 Science (1983)
Schiavi, S., Ocampo-Pineda, M., Barakovic, M., Petit, L., Descoteaux, M., Thiran, JP., Daducci, A.: A new method for accurate in vivo mapping of human brain connections using microstructural and anatomical information. Science Advances, 6 (31), (2020)
http://www.emmanuelcaruyer.com/phantomas.php
Tournier, J.-D.; Calamante, F. & Connelly, A. Improved probabilistic streamlines tractography by 2nd order integration over fibre orientation distributions. Proceedings of the International Society for Magnetic Resonance in Medicine, 1670, (2010)
Tournier, J.-D.; Calamante, F. & Connelly, A. MRtrix: Diffusion tractography in crossing fiber regions. Int. J. Imaging Syst. Technol., 22, 53-66 (2012)
Aydogan DB, Shi Y. Parallel Transport Tractography. IEEE Trans Med Imaging. 40(2):635-647 (2021)
Maier-Hein, Klaus, Neher, Peter, Houde, Jean-Christophe, Caruyer, Emmanuel, Daducci, Alessandro, Dyrby, Tim, Stieltjes, Bram, & Descoteaux, Maxime: Tractography Challenge ISMRM 2015. (2015)
D. C. Van Essen, S. M. Smith, D. M. Barch, T. E. J. Behrens, E. Yacoub, K. Ugurbil; WU- Minn HCP Consortium, The WU-Minn human connectome project: An overview. 62–79 (2013)
Figures