0878
BundleAtlasing: unbiased population-specific atlasing of bundles in streamline space1Biomedical Engineering Department, Mondragon Unibertsitatea, Mondragón, Spain, 2Department of Intelligent Systems Engineering, Indiana University Bloomington, Bloomington, IN, United States
Synopsis
White matter bundle atlases play a crucial role in the segmentation of bundles and the understanding of brain connectomes. However, the construction of streamline atlases that accurately represent the underlying population anatomy is challenging. In this work, we present BundleAtlasing, a new method to compute population-specific bundle atlases in the space of streamlines. The proposed approach is based on two key aspects: an iterative groupwise unbiased bundle registration, and a pairwise bundle combination strategy. We show that our method is able to correctly generate unbiased atlases that represent the average group anatomy of a population.
Introduction
One of the main applications of diffusion magnetic resonance imaging is determining how white matter structures vary both within and across populations (e.g., healthy vs. disease). In this sense, white matter atlases are a useful tool as they aggregate information across subjects and serve as a reference template for bundle reconstruction. In recent years, white matter atlases have been created for diffusion metrics1 and bundles in both image2 and streamline space3,4. However, most of these were built using image-based registration (as opposed to direct bundle registration) or used template-based registration, which might result in spatially biased atlases. In fact, there are few open-source tools available5 to compute population-specific white matter bundle templates. Here, we present BundleAtlasing, a new method for creating unbiased white matter bundle atlases in the space of streamlines. The developed tool will be available as part of the DIPY library6.Atlasing method
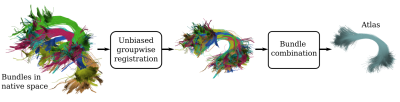
The proposed atlasing method is based on two building blocks: unbiased groupwise registration and pairwise bundle combination as shown in Fig. 1.The first stage aims to register all bundles to a common space that is not biased towards any specific subject, and thus, an iterative groupwise linear bundle registration method is proposed. This approach extends the streamline-based linear registration (SLR) method7. Starting with a pair of bundles in native space (Fig. 2A), the common approach is to consider one of the bundles as a reference (i.e. static) and compute the transformation matrix (T) that maps the coordinates of the moving bundle to the static bundle (Fig. 2B). This is useful for applications where an atlas has already been defined but is not appropriate when the intention is to create a new atlas. To overcome this, our proposed unbiased bundle registration adds an extra step: after computing the full transformation, a halfway transformation (T1) is obtained by considering only half of the computed transformation parameters:
$$translation’ = translation/2\\rotation’ = rotation/2\\scaling’ = (1+scaling)/2\\shearing’ = shearing/2$$
Then, the reciprocal transformation (T2) is computed following the same procedure, but switching the bundle considered as static. To prevent undesired shrinking effects, transformation parameters are normalized so that the mean translation, rotation, and shearing is zero, and the product of each scaling parameter is one.
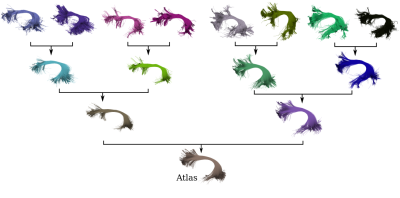
To accomplish groupwise registration the aforementioned process is applied iteratively. In each iteration, bundles are registered in pairs to the halfway space. The bundles become closer to each other with each iteration, until the process converges and the bundles are considered to be in a common space. In the second stage of BundleAtlasing, bundles are combined into a single atlas using a tree-like pairwise combination strategy as shown in Fig. 3. At each tree level, bundles are randomly shuffled and combined in pairs. When the last level is reached, the resulting bundle is considered as the population-specific atlas. To combine a pair of bundles, streamlines from both bundles are matched in pairs solving the rectangular linear assignment problem8, which matches pairs of streamlines by minimizing the sum of the distances. After that, matched streamlines are averaged and unmatched streamlines are retained unchanged.
Experiments and results
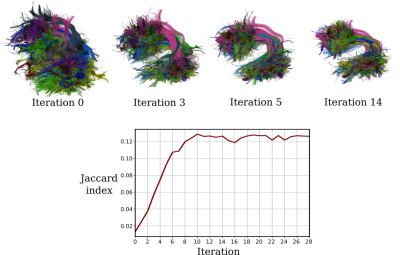
The developed method was tested on the segmented left arcuate fasciculi of 32 healthy subjects from an open-source Parkinson’s Progression Markers Initiative dataset9-11.First, the convergence of the groupwise unbiased registration was tested. To this end, all 32 bundles were iteratively registered as previously described. During the process, the quality of the alignment was examined both visually and numerically by measuring the average Jaccard index between all bundle pairs. As shown in Fig. 4, the iterative registration procedure converges to a common space after 10 iterations.
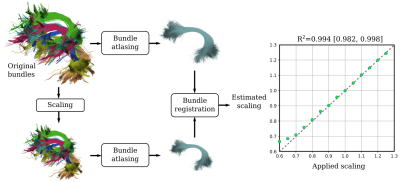
Secondly, it is crucial that obtained atlases reflect the population anatomy accurately so that they can be used for group comparisons. Thus, we tested the capacity of BundleAtlasing to differentiate populations with different average bundle size (Fig. 5). First, values of isotropic scaling from 0.6 to 1.3 were applied to the original bundles to create structurally different groups mimicking a real-case scenario such as an infant vs. adult study. Then, for every group, an atlas was computed and registered to the atlas derived from the original bundles. From each registration, an estimation of the applied scaling was retrieved. Importantly, we found a close relationship (R2=0.994) between the applied and estimated scaling, which demonstrates that the obtained atlases are able to capture structural differences in scaling.
Discussion
In this work, a novel unbiased bundle atlasing method called BundleAtlasing is presented. We show that the proposed approach is able to construct population-specific atlases in an unbiased fashion in streamline space. BundleAtlasing will be freely available in the DIPY library and has multiple potential applications. In particular, it could be well suited to compute atlases of populations differing from the commonly employed standard spaces (e.g., infants or the elderly). It may also be useful to visualize and quantify anatomical differences between groups. Furthermore, the proposed groupwise registration is not restricted to bundles and could be generalized to image atlasing as well. Future work will focus on adding non-rigid registration12 into the pipeline and testing the method on a larger collection of bundles.Acknowledgements
This research has received funding from the 2021 Google Summer of Code program.References
1. Varentsova A, Zhang S, Arfanakis K, Development of a high angular resolution diffusion imaging human brain template. NeuroImage. 2014;91:177-186
2. Hansen C.B., Yang Q, Lyu I, et al. Pandora: 4-D White Matter Bundle Population-Based Atlases Derived from Diffusion MRI Fiber Tractography. Neuroinform. 2021;19:447-460.
3. Yeh F, Panesar S, Fernandes D, et al. Population-averaged atlas of the macroscale human structural connectome and its network topology. Neuroimage. 2018;178:57-68.
4. Zhang F, Wu Y, Norton I, et al. An anatomically curated fiber clustering white matter atlas for consistent white matter tract parcellation across the lifespan. Neuroimage. 2018;179:429-447.
5. O’Donnell LJ, Wells WM, Golby AJ, et al. Unbiased Groupwise Registration of White Matter Tractography. In: Ayache N, Delingette H, Golland P, Mori K. (eds) Medical Image Computing and Computer-Assisted Intervention – MICCAI 2012. Lecture Notes in Computer Science, vol 7512. Springer, Berlin, Heidelberg.
6. Garyfallidis E, Brett M, Amirbekian B, et al. Dipy, a library for the analysis of diffusion MRI data. Front Neuroinform. 2014;8:8.
7. Garyfallidis E, Ocegueda O, Wasserman D, Descoteaux M, Robust and efficient linear registration of white-matter fascicles in the space of streamlines. NeuroImage. 2015;117:124-140.
8. Olivetti E, Gori P, Astolfi P, et al. Nonlinear Alignment of Whole Tractograms with the Linear Assignment Problem. In: Špiclin Ž, McClelland J, Kybic J, Goksel O. (eds) Biomedical Image Registration. WBIR 2020. Lecture Notes in Computer Science, 2020;12120. Springer, Cham.
9. Chandio, BQ, DIPY Processed Parkinson's Progression Markers Initiative (PPMI) Data Derivatives. The NIH Figshare Archive. Dataset. https://doi.org/10.35092/yhjc.12033390.v1; 2020
10. Chandio BQ, Risacher SL, Pestilli F et al. Bundle analytics, a computational framework for investigating the shapes and profiles of brain pathways across populations. Sci Rep. 2020;10:17149.
11. Marek K et al. The Parkinson progression marker initiative (PPMI), Prog. Neurobiol. 2011;95:629-635.
12. Chandio BQ, Garyfallidis E, StND: Streamline-based Non-rigid partial-Deformation Tractography Registration. Medical Imaging Meets NeurIPS. 2020.
Figures