0868
Mapping Rodent Brain Mechanical Properties In Vivo with Magnetic Resonance Elastography and Nonlinear Inversion1Biomedical Engineering, University of Delaware, Newark, DE, United States, 2Psychological & Brain Sciences, University of Delaware, Newark, DE, United States, 3Thayer School of Engineering, Dartmouth College, Hanover, NH, United States
Synopsis
Developing preclinical MRE techniques that are comparable to human MRE is important for translational studies. This pilot study investigates the efficacy of the nonlinear inversion algorithm on rat brain MRE data. Whole-brain MRE scans were performed on female, Long-Evans rats using a custom MRE-EPI sequence and piezoelectric actuator with a resolution of 0.25 mm isotropic and with 600 Hz vibration. NLI parameters were adjusted for brain size and frequency. The resulting shear stiffness and damping ratio maps exhibited strong contrast between different anatomical regions. These results validate the use of NLI in preclinical MRE settings.
Introduction
High-resolution, preclinical MR imaging is important for developing studies translatable to humans. Magnetic resonance elastography (MRE) is a technique for noninvasively imaging brain mechanical properties and has been used in several animal models to examine brain tissue integrity in disease.1 However, many preclinical MRE studies do not use comparable methods as in the human brain, such as high-resolution imaging and inversion techniques. In particular, the finite element-based nonlinear inversion algorithm (NLI)2 has been used extensively on human MRE data to generate spatially-resolved mechanical property maps with high fidelity,3 but its efficacy in preclinical settings has yet to be determined. MRE and NLI outcomes of shear stiffness and damping ratio have shown effects in aging, Alzheimer’s disease, and relationships to behavior.4-6 Similar approaches using animal models can aid in determining the neurobiological bases of these effects. In this study, we validate the use of whole-brain MRE with NLI to measure mechanical properties of the rat brain in vivo for the first time.Methods
Animal PreparationWild-type, female, Long-Evans rats (n=2) were anesthetized using 1 – 3% isoflurane as prescribed in the approved IACUC protocol. Body temperature and respiration rate were monitored throughout the entire scanning session. Total scan time was one hour. Vibrations were applied via a nonmagnetic, piezoelectric actuator (APA150M; Cedrat Technologies, Meylan, France). A custom holder and adjustable bite bar transmitted waves from the actuator to the rodent’s brain (Figure 1).
MRE Imaging
All scans were conducted on a 9.4T Bruker BioSpec preclinical imaging system (Bruker Corporation, Billerica, MA). To capture 3D wave motion, a custom MRE-EPI sequence was used with motion encoding gradients applied in three directions, four phase offsets, and positive and negative gradient polarities for a total of 24 repetitions per image. Motion encoding gradients were frequency matched to the actuator vibration of 600 Hz. Magnitude and phase images were acquired using the following imaging parameters: TE/TR = 60/6800 ms, slices = 80, slice thickness = 0.25 mm, FOV = 20 x 20 mm2, matrix = 80 x 80, averages = 12, resolution = 0.25 mm isotropic. Total MRE scan time was 32 minutes.
Mechanical Property Estimation
The isotropic, nearly incompressible NLI was used to determine mechanical properties from MRE displacement data. NLI iteratively solves the Navier equation inverse problem via a finite element mesh and subzone estimation scheme. Starting from an initial property guess, subzone displacement fields are calculated and compared to measured displacements, and property distributions are iteratively updated until the error between the displacement fields is minimized. NLI outputs storage modulus (𝐺') and loss modulus (𝐺'') which are the real and imaginary components of complex shear modulus (𝐺 = 𝐺′ + 𝐺'').7,8 These parameters were then used to calculate shear stiffness (𝜇=2|𝐺|2/(𝐺′+|𝐺|)) and damping ratio (𝜉=𝐺′′/2𝐺′). The following NLI parameters were used in this study: initial property guesses of 𝐺0' = 5 kPa and 𝐺0'' = 1 kPa; subzone size = 3 mm3; spatial filtering width = 0.18 mm. These parameters were modified from typical parameters for the human brain for the size of the rat brain and frequency of vibration. Voxel-wise material property maps were generated.
Results & Discussion
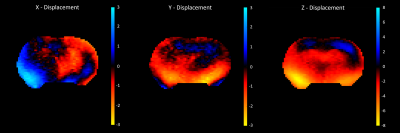
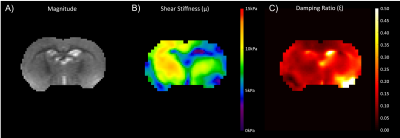
Figure 2 shows displacement maps exhibiting strong wave motion in all three directions. Figure 3B shows the outcome shear stiffness map exhibiting high contrast between the different anatomical regions, as compared to the corresponding MRE magnitude image (Figure 3A). The hippocampi in particular were much softer than the surrounding tissue. However, the right brain had significantly higher stiffness than the left which may have been due to wave motion artifacts during inversion. The damping ratio maps yielded similar property contrast, but the left brain had higher damping ratio than the right. Similarly, the hippocampal regions were clearly visible due to their high damping ratio (Figure 3C). While these MRE displacement data are at the highest spatial resolution with whole-brain coverage, to our knowledge, further opportunities are available to increase the vibration frequency and further reduce spatial filtering which may improve the ability to detect small regions with different mechanical properties.Conclusion
This pilot study validates using NLI with in vivo rat brain MRE data to estimate shear stiffness and damping ratio. NLI offers advantages in resolution and stability which improve the accuracy and reliability of property estimates. As NLI is compatible with both clinical and preclinical data at similarly high resolutions, results from animal models may be translated to humans. In addition, NLI gives access to other material models including transversely isotropic which yields better results in tissues with aligned fibers.9 Future work will include studies on developing rats and neurodegenerative diseases using transversely isotropic NLI.Acknowledgements
NIH grants R01-EB027577 and R01-AG058853 awarded to Dr. Curtis Johnson
NIH/NIAAA grant R01-AA027269 awarded to Dr. Anna Klintsova
References
1. Bayly P V., Garbow JR. Pre-clinical MR elastography: principles, techniques, and applications. J Magn Reson. 2018;291:73-83.
2. McGarry MDJ, Van Houten EEW, Johnson CL, Georgiadis JG, Sutton BP, Weaver JB, Paulsen KD. Multiresolution MR elastography using nonlinearinversion. Med Phys. 2012;39:6388–6396.
3. Johnson CL, Schwarb H, D.J. McGarry M, et al. Viscoelasticity of subcortical gray matter structures. Hum Brain Mapp. 2016;37(12):4221-4233.
4. Schwarb H, Johnson CL, McGarry MDJ, Cohen NJ. Medial temporal lobe viscoelasticity and relational memory performance. Neruoimage. 2016;132(May):534-541.
5. Hiscox L V, Johnson CL, McGarry MDJ, et al. Mechanical property alterations across the cerebral cortex due to Alzheimer’s disease. Brain Commun. 2020;2(1):1-16.
6. Delgorio PL, Hiscox L V., Daugherty AM, et al. Effect of Aging on the Viscoelastic Properties of Hippocampal Subfields Assessed with High-Resolution MR Elastography. Cereb Cortex. 2021;31(6):2799-2811.
7. Van Houten EEW, Miga MI, Weaver JB, Kennedy FE, Paulsen KD. Three-dimensional subzone-based reconstruction algorithm for MR elastography. Magn Reson Med. 2001;45(5):827-837.
8. McGarry MDJ and Van Houten EEW. Use of a Rayleigh damping model in elastography. Med Biol Eng Comput. 2008;46(8):759-766.
9. McGarry M, Houten E Van, Guertler C, et al. A heterogenous, time harmonic, nearly incompressible transverse isotropic finite element brain simulation platform for MR elastography. Phys Med Biol. 2021;66(5).