0866

Optimized denoising and removal of partial-Fourier induced Gibbs ringing improves accuracy and robustness of DTI and DKI parameters
Jenny Chen1, Benjamin Ades-aron1, Hong-Hsi Lee2, Durga Kullakanda1, Saurabh Maithani1, Dmitry S. Novikov1, Jelle Veraart1, and Els Fieremans1
1Department of Radiology, NYU School of Medicine, New York, NY, United States, 2Athinoula A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Boston, MA, United States

Synopsis

Diffusion MRI (dMRI) is affected by noise and by artifacts such as Gibbs ringing and distortions. Using software phantoms as ground-truth, this study compares diffusion tensor imaging (DTI) and diffusional kurtosis imaging (DKI) parameter estimates to assess accuracy of various denoising and Gibbs removal methods, two key components of dMRI pipelines. An optimized Diffusion parameter EStImation with Gibbs and NoisE Removal (DESIGNER) pipeline is proposed, with non-local patch MP-PCA denoising and Removal of Partial-fourier induced Gibbs Ringing (RPG), that yields more accurate metrics, fewer outlier voxels in phantoms and more robust DTI/DKI maps in patient data.

Introduction

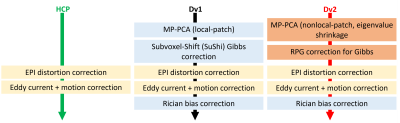
dMRI are corrupted by the effect of thermal noise and various imaging artifacts such as Gibbs ringing and distortions. To improve reproducibility and data fidelity, various dMRI pre-processing pipelines [1,2,3,4,5] are proposed that differ in artifacts they choose to address and/or the algorithmic methods, which potentially may lead to conflicting findings in clinical dMRI studies [6,7]. Here, we introduce DESIGNER 2.0 (Dv2), based on previously validated DESIGNER [1] pipeline, that additionally (1) corrects for Gibbs ringing due to partial Fourier (PF) acquisitions, which is common in clinical (research) settings, and (2) removes noise more effectively. We systematically evaluate accuracy and precision of these new steps using in-vivo dMRI and phantoms for ground-truth comparison.

Methods

We evaluated the accuracy and precision of Dv2 by comparing to (i) a minimal preprocessing pipeline (1; HCP) and (ii) the original implementation of DESIGNER (Dv1) using clinical data and simulation.

DESIGNER 2.0 is a revision of Dv1 that integrates the latest denoise and Gibbs removal development: (a) MP-PCA nonlocal-patch denoising, which selects similar voxels within a local-patch to reconstruct denoised voxel signals, with eigenvalue shrinkage [8] and (b) Removal of Partial-fourier induced Gibbs Ringing (RPG) [9].

Clinical Data: dMRI data (5 b=0 images AP, 1 b=0 image PA for distortion correction [10,11], b=250 s/mm2 – 4 directions, b=1000 s/mm2 – 20 directions, b=2000 s/mm2 – 60 directions, TE=70ms, TR=3.7s, 50 slices, resolution=1.7x1.7x3mm3, 6/8 PF) was retrospectively analyzed of a 47-year-old female who underwent MRI on a Magnetom Prisma 3T.

Simulation I: An HCP phantom [2] was modified by generating B0 and DKI tensor (weighted linear least square (WLLS) fit [12]) using the diffusion vectors matching the dMRI protocol above, and adjusting the resolution (72 slices, resolution=2.5x2.5x2.5mm3). Then, 50 sets of noisy phantoms with SNR ranging from 10 to 100 were created by adding Rician noise. Each noisy phantom was processed with HCP (no denoising), local denoising [13,14] (Dv1), or non-local denoising with eigenvalue shrinkage (Dv2), as well as pre-processed with only Rician correction [15], local denoising with eigenvalue shrinkage, and non-local denoising without eigenvalue shrinkage.

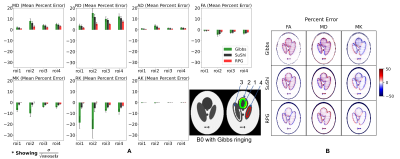
Simulation II: HCP data is acquired with PF on, hence the HCP phantom cannot evaluate PF-induced Gibbs removal methods. Instead, Gibbs ringing was introduced by k-space truncation and PF 6/8 in the horizontal direction using the Shepp-Logan phantom. The Gibbs phantom was either not corrected (HCP), corrected with Subvoxel-shifts (SuShi) method [16] (Dv1), or with RPG degibbs (Dv2). Additionally, the subject's MRI was processed with SuShi method and RPG degibbs (along with eddy and EPI correction) to see effect of degibbs on realistic anatomical structures.

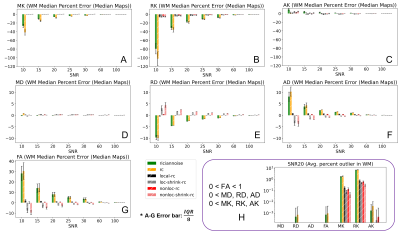
Experiments: DTI (MD – mean diffusivity, RD – radial diffusivity, AD – axial diffusivity, and FA – fractional anisotropy) and DKI (MK – mean kurtosis, RK – radial kurtosis, AK – axial kurtosis) parameter maps were estimated using WLLS fitting. For the phantoms, percent error or median percentage error (MdPE) over median of 50 noise iterations were calculated against their respective ground truth DTI/DKI maps. Average outlier percentage were computed to quantify amount of “black voxels” remaining after denoising, where outliers are defined as D, K<0 or FA>1. JHU white matter (WM) atlas labels [17] were warped to the ground truth FA map and combined to form an overall WM region of interest (ROI). Then, median value in the WM ROI was extracted from DTI/DKI MdPE maps. For Gibbs phantom, mean percent error (MPE) was taken over manually drawn ROIs.

Results

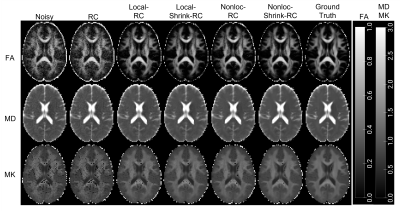
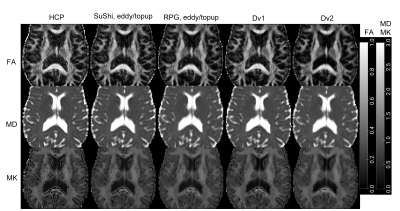
Figure 2 plots the DTI/DKI MdPE of noisy HCP phantoms pre-processed with varying denoise methods. Not denoising or Rician bias correcting alone result in the highest bias, while nonlocal-patch denoising was most accurate. Interestingly, while eigenvalue shrinkage causes bias, it results in fewest outliers. Visual comparison of the maps (Figure 3) shows eigenvalue shrinkage and nonlocal-patch maps are noticeably less noisy and with more "black voxels" removed. Figure 4a shows DTI/DKI-parameters in Gibbs phantom are least accurate without any Gibbs correction and most accurate with RPG degibbs. Although SuShi method removes some Gibbs ringing, RPG additionally removes Gibbs ringing due to PF [9,16] (Figure 4b). PF-induced Gibbs ringing can also be seen in the subject’s (Figure 5) as a dark (MD) or bright (FA) band and black voxels (MK) at the CC/CSF boundary (Figure 5). These artifacts are reduced the most in maps with RPG while Dv2 results in least noisy maps and the fewest outliers.

Discussion and Conclusion

Our results suggest nonlocal denoising and RPG degibbs can improve accuracy and precision, yielding more robust DTI/DKI maps. Of the denoising methods, nonlocal-patch denoising outperforms local-patch denoising with the lowest MdPE. Although eigenvalue shrinkage causes some bias in estimations, it also removes the most outliers and gives the least noisy parametric maps, making it the preferred method for voxel-based analysis. To correct for Gibbs ringing in PF 6/8 datasets, RPG gives the smallest MPE and cleaner maps.

As expected from the phantom results, comparing the three pipelines on subject data (Figure 5), Dv2, which involves RPG and nonlocal-patch denoising with eigenvalue shrinkage, performed best, as the parametric maps show the least outlier and noise. Future work will optimize estimation methods [12,18] to target remaining "black voxels" in kurtosis maps.

Acknowledgements

Research was supported by the National Institute of Neurological Disorders and Stroke of the NIH under awards R01 NS088040 and R01 EB027075, and by the Hirschl foundation and was performed at the Center of Advanced Imaging Innovation and Research (CAI2R, www.cai2r.net), a Biomedical Technology Research Center supported by NIBIB with the award P41 EB017183.

References

  1. Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, Van Essen DC, Jenkinson M; WU-Minn HCP Consortium. The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage. 2013 Oct 15;80:105-24. doi: 10.1016/j.neuroimage.2013.04.127. Epub 2013 May 11. PMID: 23668970; PMCID: PMC3720813.
  2. Ades-Aron, B., Veraart, J., Kochunov, P., McGuire, S., Sherman, P., Kellner, E., Novikov, D. S., & Fieremans, E. (2018). Evaluation of the accuracy and precision of the diffusion parameter EStImation with Gibbs and NoisE removal pipeline. NeuroImage, 183, 532–543. https://doi.org/10.1016/j.neuroimage.2018.07.066
  3. Pierpaoli C, Irfanoglu LW,MO, Barnett A, Basser P, Chang L-C, Koay C, Pajevic S, Rohde G, Sarlls J, and Wu M, 2010. TORTOISE: an integrated software package for processing of diffusion MRI data ISMRM, Stockholm, Sweden.
  4. Cieslak, M., Cook, P.A., He, X. et al. QSIPrep: an integrative platform for preprocessing and reconstructing diffusion MRI data. Nat Methods 18, 775–778 (2021). https://doi.org/10.1038/s41592-021-01185-5
  5. Maximov, II, Alnæs, D, Westlye, LT. Towards an optimised processing pipeline for diffusion magnetic resonance imaging data: Effects of artefact corrections on diffusion metrics and their age associations in UK Biobank. Hum Brain Mapp. 2019; 40: 4146– 4162. https://doi.org/10.1002/hbm.24691
  6. Chen J, Ades-aron B, et al., The effect of image pre-processing pipelines on age associations of diffusion and kurtosis in white matter, International Society for Magnetic Resonance in Medicine, 2021, Digital Poster (presentation May 2021)
  7. Z. Lu, W. Huang and C. Guan, "A comparison of DTI pre-processing tools on a dataset of chronic subcortical stroke rehabilitation patients," 2017 8th International IEEE/EMBS Conference on Neural Engineering (NER), 2017, pp. 568-571, doi: 10.1109/NER.2017.8008415.
  8. M. Gavish and D. L. Donoho, "Optimal Shrinkage of Singular Values," in IEEE Transactions on Information Theory, vol. 63, no. 4, pp. 2137-2152, April 2017, doi: 10.1109/TIT.2017.2653801.
  9. Lee HH, Novikov DS, Fieremans E. Removal of partial Fourier-induced Gibbs (RPG) ringing artifacts in MRI. Magn Reson Med. 2021 Nov;86(5):2733-2750. doi: 10.1002/mrm.28830. Epub 2021 Jul 5. PMID: 34227142.
  10. J.L.R. Andersson, S. Skare, J. Ashburner. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. NeuroImage, 20(2):870-888, 2003.
  11. S.M. Smith, M. Jenkinson, M.W. Woolrich, C.F. Beckmann, T.E.J. Behrens, H. Johansen-Berg, P.R. Bannister, M. De Luca, I. Drobnjak, D.E. Flitney, R. Niazy, J. Saunders, J. Vickers, Y. Zhang, N. De Stefano, J.M. Brady, and P.M. Matthews. Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage, 23(S1):208-219, 2004.
  12. J. Veraart, J. Sijbers, S. Sunaert, A. Leemans, B. Jeurissen, Weighted linear least squares estimation of diffusion MRI parameters: strengths, limitations, and pitfalls. NeuroImage 81, 335-346 (2013).
  13. Cordero-Grande, L.; Christiaens, D.; Hutter, J.; Price, A.N.; Hajnal, J.V. Complex diffusion-weighted image estimation via matrix recovery under general noise models. NeuroImage, 2019, 200, 391-404, doi: 10.1016/j.neuroimage.2019.06.039 4.
  14. Veraart, J., Novikov, D. S., Christiaens, D., Ades-Aron, B., Sijbers, J., & Fieremans, E. (2016). Denoising of diffusion MRI using random matrix theory. NeuroImage, 142, 394–406. https://doi.org/10.1016/j.neuroimage.2016.08.016 5.
  15. Koay CG, Basser PJ, 2006. Analytically exact correction scheme for signal extraction from noisy magnitude MR signals. Journal of Magnetic Resonance 179, 317–322.
  16. Kellner E, Dhital B, Kiselev VG, Reisert M. Gibbs-ringing artifact removal based on local subvoxel-shifts. Magn Reson Med. 2016 Nov;76(5):1574-1581. doi: 10.1002/mrm.26054. Epub 2015 Nov 24. PMID: 26745823.
  17. Hua et al., Tract probability maps in stereotaxic spaces: analysis of white matter anatomy and tract-specific quantification. NeuroImage, 39(1):336-347 (2008)
  18. Henriques RN, Jespersen SN, Jones DK, Veraart J. Toward more robust and reproducible diffusion kurtosis imaging. Magn Reson Med. 2021 Sep;86(3):1600-1613. doi: 10.1002/mrm.28730. Epub 2021 Apr 8. PMID: 33829542; PMCID: PMC8199974.

Figures

Figure 1. Step-by-step flow diagram for HCP, Dv1, and Dv2 pipeline.

Figure 2. A-G: Bar plots showing median and interquartile range (error bar scaled by 1/8) of DTI/DKI parameters MdPE (median percentage error) in WM of median of 50 sets of phantoms (SNR from 10-100). H: Average percent outlier (WM) of 50 phantom iterations (SNR 20). Noisy phantoms were left noisy or processed with varying denoising methods. Nonlocal denoising is most accurate (A-G) while nonlocal denoising with eigenvalue shrinkage has fewest outliers (H). rc=Rician correction, local=local patch, nonlocal=nonlocal patch, shrink=eigenvalue shrinkage

Figure 3. FA, MD, and MK maps for ground truth HCP phantom and noisy phantom (SNR 20) with varying denoising methods. Maps for non-local denoising with eigenvalue shrinkage appears to have the least black voxels. RC=Rician correction, local=local patch, nonloc=nonlocal patch, shrink=eigenvalue shrinkage

Figure 4. DTI/DKI MPE compared between Shepp-Logan phantom with Gibbs ringing and Gibbs ringing with SuShi method and RPG degibbs. A: Bar plots showing ROIs’ MPE and standard error in DTI/DKI parameter maps. RPG degibbs has the smallest percent error. B: FA, MD, and MK, MPE maps. Although SuShi method removes Gibbs ringing, RPG degibbs removes additional ringing due to PF. Gibbs ringing was simulated from k-space truncation and 6/8 PF in the horizontal direction.

Figure 5. FA, MD, and MK maps from a healthy 47-year-old female pre-processed with varying pipelines. RPG degibbs removes the dark (MD) and bright (FA) band and the largest number of black voxels (MK) in GCC/CSF and SCC/CSF boundary, where Gibbs ringing dominates. Maps from Dv2 pipeline appears to have the least noise. SuShi = SuShi method, RPG = RPG degibbs

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)
0866
DOI: https://doi.org/10.58530/2022/0866