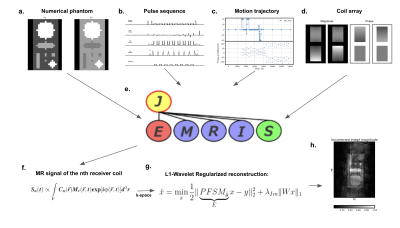
0862
On the limits of model-based reconstruction for retrospective motion correction in the presence of spin history effects1Department of Diagnostic and Interventional Radiology, School of Medicine, Technical University of Munich, Munich, Germany
Synopsis
MRI reconstruction methods comprising model-based motion correction modules often rely on the assumption of absence or piecewise constant motion patterns during signal readout and on the insignificance of spin history effects. Furthermore, the success of such methods also depends on the characteristics and motion sensitivity of the employed sequence and measured tissue properties and may therefor limit the general utility of such approaches in a clinical context. The present study demonstrates the limitations of Fourier-model-based motion correction reconstruction schemes by subtle violations of the piecewise constant motion assumption using Bloch simulations a model-based motion-corrected reconstruction approach.
Synopsis
MRI reconstruction methods comprising model-based motion correction modules often rely on the assumption of absence or piecewise constant motion patterns during signal readout and on the insignificance of spin history effects. Furthermore, the success of such methods also depends on the characteristics and motion sensitivity of the employed sequence as well as tissue properties which may limit the general utility of such approaches in a clinical context. The present study demonstrates the limitations of Fourier-model-based motion correction reconstruction schemes by subtle violations of the piecewise constant motion assumption using Bloch simulations.Summary of Main Findings
The common assumption of piecewise constant motion during readout which would allow modeling of motion-induced signal modulations by simple image transformations in combination with Fourier transformations can be violated and might need to be adjusted in the presence of intra-shot motion effects.Introduction/Purpose
The reconstruction of motion corrupted images – even for rigid motion – poses a demanding reconstruction challenge in MRI1. The idea of retrospective model-based motion correction approaches is to impose modelling assumptions on the origin of the motion-induced signal modulations and therefore potentially allow to make use of data that would otherwise have been discarded as corrupted data. Due to this data recovery potential, model-based motion correction methods are very desirable for motion correction in undersampled MR acquisition schemes or the ones that can only achieve limited SNR. The estimation of motion-induced signal modulations can be demanding in terms of computation, memory requirement and modelling, requiring a good idea about expedient assumptions and simplifications. The signal evaluation including spin history effects can be precisely calculated using Bloch simulations, the computational cost of doing so usually prevent the solving of Bloch equations in iterative reconstruction methods. A common assumption is therefore to assume that the motion trajectory is approximately piecewise static during the readout, which allows to use simple image transformations in combination with Fourier transformations to estimate motion induced signal modulations. Therefore, the purpose of present study was to demonstrate the limitations of the FSRM approach for the purpose of retrospective rigid motion correction in a clinically used 2D multi-shot TSE acquisition scheme.Methods
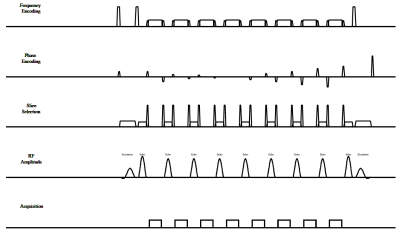
Bloch simulations of rigid motion artifacts 2D multi-shot TSE acquisition scheme was exported from a clinical MR scanner. A sequence diagram and parameter details are given in Figure 2. A numerical phantom with properties outlined in Figure 1 was used throughout all simulations. The Bloch simulations were carried out using JEMRIS2.8.3.4 For the purpose of challenging the validity of the FSRM-approach, two motion trajectories were defined: one in agreement with the general assumption of the absence of motion during signal readout and one purposely violating this assumption by assuming a continuous positional change during readout. (see motion trajectories in Figure 3). Furthermore, four coil channels were simulated to allow for a realistic parallel imaging scenario. The potential impact on motion model-based reconstruction schemes was investigated using the Bloch-simulated signal in a motion-correcting least-squares minimization formulation embedded in a compressed sensing formulation:$$[\hat{x},\hat{\theta}]=\min_{x,\theta}\frac{1}{2}\|\underbrace{PFSM_{\theta}}_{E}x-y\|_2^2+\lambda_{Im}\|Wx\|_1+\lambda_{Mo}\|\theta\|_2^2$$, where $M=TR$, T and R are translation and rotation motion operators, S - coil sensitivity operator, F - Fourier Transform, P - sampling operator, $\lambda_{Im}$ and $\lambda_{Mo}$ are regularization parameters for the image and motion respectively. Rotational transformations were applied using a previously introduced convolution-based interpolation technique4,5. From an implementation point of view, the joint optimization was divided in a least-squares optimization $$\hat{\theta}=\min_{\theta}\frac{1}{2}\| \underbrace{PFSM_{\theta}}_{E}\hat{x}-y \|_2^2+\lambda_{Mo}\|\theta\|_2^2,$$ and a gradient decent wavelet-regularized reconstruction $$\hat{c}= \min_c \frac{1}{2} \| \underbrace{P F S M_{\hat{\theta}} W^H}_{A} c - y \|_2^2 + \lambda_{Im} \| c \|_1$$where $$ \hat{{x}}=W^H \hat{c} $$ and c are the wavelet coefficients. The algorithm was implemented using sigpy6.
Results/Discussion
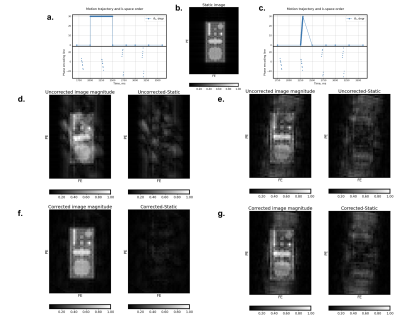
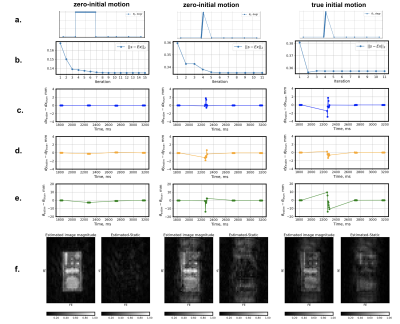
From Figure 1, in the case of intershot motion, when the object remains stationary within the lines in one echo train and moves only in-between the shots, the reconstruction with the ground truth motion (f) is able to correct for the motion-induced artifacts appearing in the static reconstruction (d). Whereas for the intrashot linear motion case, the knowledge of the motion trajectory does not improve (g) the corrupted reconstructed image (e). The correction algorithm searching for motion parameters starting with zero-initial motion finds the estimates close to the ground truth for the piecewise constant motion trajectory as can be seen on parameter residual plots in the first column of (c), (d), (e). The improvement of the image by the algorithm is shown on the image difference plot (f), left. Figure 2 shows high errors of motion parameter estimates for the intrashot motion and no improvement of the reconstructed image. The change of the optimum with the start at the true motion parameters (Figure 2) indicates that the loss function in case of intrashot motion has a better minimum than the true motion, which can point to the model failure at describing the Bloch simulated data.Acknowledgements
The authors would like to thank you Tom Geraedts for sharing his experience and code for the conversion of MR scanner sequences to JEMRIS sequence definition files with us. The present work was supported by DAAD (Project number: 57514573). The authors also acknowledge research support from Philips Healthcare.References
1. Godenschweger, F., Kägebein, U., Stucht, D., Yarach, U., Sciarra, A., Yakupov, R., Lüsebrink, F., Schulze, P., & Speck, O. (2016). Motion correction in MRI of the brain. Physics in Medicine and Biology, 61(5), R32–R56. https://doi.org/10.1088/0031-9155/61/5/R32
2. Batchelor, P. G., Atkinson, D., Irarrazaval, P., Hill, D. L. G., Hajnal, J., & Larkman, D. (2005). Matrix description of general motion correction applied to multishot images. Magnetic Resonance in Medicine, 54(5), 1273–1280. https://doi.org/10.1002/mrm.20656
4. Stöcker, T., Vahedipour, K., Pflugfelder, D., & Shah, N. J. (2010). High-performance computing MRI simulations. Magnetic Resonance in Medicine, 64(1), 186–193. https://doi.org/10.1002/mrm.22406
5. Unser, M., Thévenaz, P., & Yaroslavsky, L. (1995). Convolution-Based Interpolation for Fast, High-Quality Rotation of Images. IEEE Transactions on Image Processing, 4(10), 1371–1381. https://doi.org/10.1109/83.465102
6. Toffoli, T., & Quick, J. (1997). Three-Dimensional Rotations by Three Shears. Graphical Models and Image Processing, 59(2), 89–95. https://doi.org/10.1006/gmip.1997.0420
6. SigPy v0.1.23
Figures