Introduction

In conventional clinical MRI, images are reconstructed under the assumption that linear spatial gradient encoding has operated on MR signals [1]. However, the engineering constraints on gradient coil performance and system efficiency make generating linear gradient fields across the entire field of view (FOV) impractical [2]. The presence of gradient field nonlinearity (GNL) causes image distortions and is particularly problematic for MRI-guided radiotherapy treatment where anatomy must be localized with sub millimetre precision [3]. Image distortions can be corrected by image-domain interpolation [1] or k-space domain reconstruction [2] method. However, computational complexity limits their application for real-time tumor tracking during treatments [4]. Our recently developed ReUINet method shows the promise of deep neural networks for fast distortion correction in the image domain [5]. In this work, to further reduce the computational cost, we propose a novel deep learning network, DFReconNet, that can reconstruct distortion free (DF) images directly from the k-space data. Simulated brain dataset and experimental phantom images acquired from an MRI-Linac were used to investigate the proposed method.

Methods

Problem formulation

The forward encoding process with gradient nonlinearity can be formulated as [6]: $$ E_{GNL}\cdot Fm=b\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(1)$$
Where b is the GNL-corrupted k-space signal; F represents theoretical Fourier transform matrix and m denotes the distortion free image. E_GNL is the GNL encoding matrix with the kernel of e_GNL =e^-2πjkΔ(L), where Δ(L) is the GNL induced spatial deviation at location L. The distortion free image can be reconstructed by the penalized regression [2]:$$m=\mathop{\arg\min}_{\ m} \{\lambda P(m)+\| E_{GNL} \cdot Fm-b\|_F^2\} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(2)$$ where P(m) denotes a regularization function with a weighting parameter λ. Optimization algorithms, e.g., nonlinear conjugate gradients, can be used to solve Eq. (2); however, they normally come with the compromise of high computational time.

DFReconNet

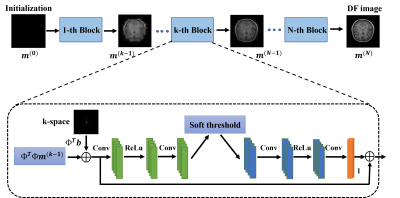
Inspired by an interpretable optimization-based network, i.e., ISTA-Net [7], we propose a distortion free reconstruction network (DFReconNet) to solve the minimization problem in Eq. (2). As shown in Figure. 1, DFReconNet consists of four iterative blocks and each block learns one iteration in ISTA algorithm. Each block starts with a data fidelity calculation, followed by a learnable nonlinear forward transform, a soft-thresholding operation, and a learnable nonlinear backward transform. The forward and backward transforms in each block were learned using the combination of a rectified linear unit (ReLU) and two convolutional layers.

Data preparation and network training

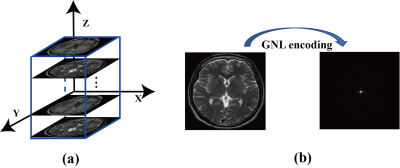
In this study, 3000 T1-weighted brain images from a public MR dataset [8] were selected as training labels. Brain images were acquired with a whole-body MRI scanner and the imaging parameters were: voxel size = 320 × 320 × 256, resolution = 0.7 mm × 0.7 mm × 0.7 mm and TE/TR = 2.13 ms/2.4 s. Twenty locations with uniform intervals (15 mm) were allocated along z direction in a FOV of 30 cm × 30 cm × 30 cm, as shown in Figure 2. Every 150 randomly selected brain images were positioned at each location and our previously developed GNLNet [4] was used to provide the GNL field information. The corresponding GNL-corrupted k-space data of each brain image was generated by using Eq. (1). Repeated operations were conducted for the other two orthogonal planes. The proposed DFReconNet was trained on an Nvidia Tesla V100 GPU (32G) for 100 epochs (~10 hours) using these simulated images with Adam optimizer.
Another 300 brain images from the same dataset were used to prepare the simulated testing data. A 3D grid phantom was scanned from the 1.0T Australian MRI-Linac system with the imaging paramters: matrix size = 130 × 110 × 192, resolution = 1.8 mm × 2 mm × 1.8 mm, and TE/TR = 15 ms/5.1 s. 192 phantom slices were obtained to validate the proposed method.

Results

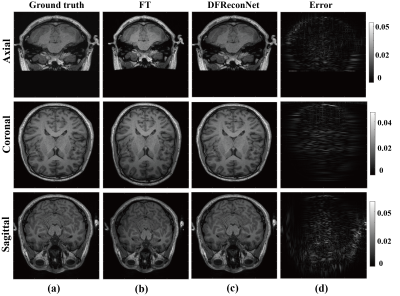
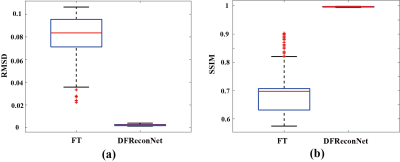
Figure 3 shows brain results reconstructed by standard Fourier transform (FT) and the proposed DFReconNet at three orthogonal planes. Compared with the ground truth images, considerable geometric distortions including image shrinkage (axial and sagittal) and dilation (coronal) are presented in Figure 3(b). By contrast, the DFReconNet successfully eliminated these distortions and resulted in negligible errors (less than 5%). The root mean square deviation (RMSD) and structural similarity index (SSIM) values were calculated on 300 testing brain images. As shown in Figure 4, the median RMSD of FT-reconstructed images is ~0.08, which is approximately 8-fold greater than that of DFReconNet results (~0.01). Similarly, increased SSIM median value was observed when using DFReconNet (~0.98) in comparison to FT method (~0.7).
Figure 5 illustrates the DFReconNet results on phantom images. Compared to the FT method, geometric distortions are successfully reduced in DFReconNet-reconstructed images, which is consistent with the results of Figure 3. The reconstruction time of the proposed network on an image of size 128 × 128 is 0.08s with an Nvidia Tesla V100 GPU (32G), which makes the proposed method feasible for real-time imaging applications.

Discussion and conclusion

Results on simulated brain dataset and experimental phantom images indicated that the proposed method was capable of reconstructing distortion free images directly from k-space domain in real-time, which can facilitate the accurate radiotherapy treatment on an MRI-Linac.