0849
Properties of 2D MR image reconstructions with deep neural networks at high acceleration rates1Facebook AI Research, New York, NY, United States, 2shaped.ai, New York, NY, United States, 3Radiology, NYU School of Medicine, New York, NY, United States, 4Artificial Intelligence in Biomedical Engineering, Friedrich-Alexander University Erlangen-Nuremberg, Erlangen, Germany, 5Facebook AI Research, Menlo Park, CA, United States
Synopsis
We assess the properties of deep neural network-reconstructed brain MR images in the high acceleration regime at factors up to 100. We have three contributions: 1) metrics on model performance from 2- to 100-fold accelerations, 2) a Monte Carlo procedure for scoring the quality of model reconstructions using only subsampled data, and 3) assessment of the acceleration effects on pathology in six cases. Our Monte Carlo procedure can estimate ground truth PSNR with coefficients of determination greater than 0.5 using only subsampled data. Our pathology results were stable in DNN reconstructions up to 8-fold acceleration.
Introduction
Reducing the time to complete an MRI examination remains a major topic of interest in medical imaging. Recently, deep learning methods have shown impressive reconstruction capabilities.1-13 Many efforts for 2D reconstruction have focused on improving parallel imaging acceleration rates from 2 to 4 or 8.1,4,7,10,13-15 We investigate the properties of reconstructions beyond this range, looking at accelerations up to 100.There are two high-acceleration regimes: 1) a “traditional” acceleration setting (A<20) with a densely-sampled center and sparsely sampled periphery and 2) a “super-resolution” regime where the rate is so high that only central k-space lines are acquired. In the super-resolution regime, the speed of an MRI is closer to a CT scan, but the artifacts can be too severe for general-purpose imaging. Our investigation seeks to understand the limitations of extreme acceleration and whether this regime could be useful for limited applications such as screening.
We have three contributions: 1) a quantitative assessment of deep learning reconstruction performance in the high acceleration regime, 2) a procedure for scoring the quality of reconstructions in the absence of ground truth via Monte Carlo (MC) reconstruction simulations, and 3) a preliminary study of image quality in six pathology cases.
Methods
Models and TrainingWe modified and enlarged the E2E Variational Network to 231 million parameters.16 A block diagram of the model structure and a description of changes is in Figure 1. We trained the model in two stages. The first stage trained for all contrasts and accelerations for 45 epochs. We investigated 12 acceleration levels between 2 and 100. In the second stage we fine-tuned a model for each tuple of (acceleration, contrast). We fine-tuned T1 models for 55 epochs, T2 models for 15 epochs, and FLAIR models for 60 epochs. Each stage used 24 GPUs for training and took about 3 days.
Both stages used a densely-sampled center (1/20 of the data) with Hermitian offset-sampling in the periphery to take advantage of weak Hermitian symmetry in the data.18 Above an acceleration of 20 we remove lines from the center beginning with the outer lines.
Analysis
After training, we ran the models on the test set at all of the accelerations under study and compared quantitative metrics of volume SSIM, PSNR, and MSE. In addition to quantitative analysis, we selected a sample of six cases for review.
Monte Carlo Simulation Procedure
We developed a procedure to estimate ground-truth metrics (SSIM and PSNR) using Monte Carlo (MC) simulations on subsampled data. Previous works in MRI have used Monte Carlo methods for error estimation.19-21 Our procedure makes no assumptions regarding the distribution of the residuals and extends earlier methods to complex-valued, multi-coil data.
Figure 2 shows the simulation. The simulation begins by estimating complex phase and coil sensitivities from the densely-sampled center. Then we apply the phase, sensitivities, forward FFT, and noise to create a fully-sampled, synthetic k-space. We randomly vary offsets to create 5 subsampled k-space realizations from the synthetic k-space, apply the model to all realizations, and then average the metric of interest using the original reconstruction as ground truth. The procedure leaves some residual bias. To compensate for this bias we fit scaling and offset regression parameters using hold-out validation data. We calculate R2 of the MC estimates on hold-out test data to assess estimation quality. We did not apply MC simulation at accelerations above 20 because these rates only sampled the k-space center.
Datasets
All experiments were performed on the brain split of the fastMRI dataset15,22 collected and de-identified by NYU. The dataset contains T1, T2, and FLAIR scans divided into train, validation, and test splits. We used a full version of the test set that will be released to the public at a later date.
Results
For reference, the proposed model (fine-tuned for equispaced sampling patterns) achieved 0.9596 SSIM at 4X and 0.9424 SSIM at 8X, which would place 2nd and 4th, respectively, on the public fastmri.org leaderboard.Plots of SSIM, PSNR, and MSE on the test set as a function of acceleration with the offset sampling pattern are shown in Figure 3. Image quality metrics deteriorate rapidly in the standard acceleration regime and more slowly in the super-resolution regime above 20X acceleration.
Figure 4 shows results of the MC procedure. MC statistical estimates are most accurate for PSNR and MSE and generally predictive of all three ground-truth metrics for all contrasts and accelerations.
Figure 5 shows three illustrative cases across accelerations comparing DNN and zero-filled reconstructions. At high accelerations up to 8, depiction of pathology is mildly affected. After crossing into the super-resolution regime, pathology becomes dramatically altered, rendering DNN-reconstructed images non-diagnostic. We found similar results in four other pathology cases (not shown).
Conclusion
We assessed DNN reconstruction models in the high acceleration setting. Our quantitative assessment identified a standard reconstruction vs. super resolution regime. The Monte Carlo procedure was predictive of ground-truth metrics using only undersampled data and could be applied to any metric, though it retains standard linear regression limitations of susceptibility to outliers. The qualitative analysis indicated that some pathologies can be stably reconstructed at accelerations up to 8.Acknowledgements
We would like to thank NIH grants R01EB024532 and P41EB017183 for supporting this research.References
Yang Y, Sun J, Li H, Xu Z. Deep ADMM-Net for compressive sensing MRI. In NeurIPS 2016 Dec 5 (pp. 10-18).
Yang G, Yu S, Dong H, Slabaugh G, Dragotti PL, Ye X, Liu F, Arridge S, Keegan J, Guo Y, Firmin D. DAGAN: Deep de-aliasing generative adversarial networks for fast compressed sensing MRI reconstruction. IEEE Transactions on Medical Imaging. 2017;37(6):1310-21.
Schlemper J, Caballero J, Hajnal JV, Price AN, Rueckert D. A deep cascade of convolutional neural networks for dynamic MR image reconstruction. IEEE Transactions on Medical Imaging. 2017;37(2):491-503.
Hammernik K, Klatzer T, Kobler E, Recht MP, Sodickson DK, Pock T, Knoll F. Learning a variational network for reconstruction of accelerated MRI data. Magnetic Resonance in Medicine. 2018;79(6):3055-71.
Aggarwal HK, Mani MP, Jacob M. MoDL: Model-based deep learning architecture for inverse problems. IEEE Transactions on Medical Imaging. 2018;38(2):394-405.
Mardani M, Gong E, Cheng JY, Vasanawala SS, Zaharchuk G, Xing L, Pauly JM. Deep generative adversarial neural networks for compressive sensing MRI. IEEE Transactions on Medical Imaging. 2018;38(1):167-79.
Lee D, Yoo J, Tak S, Ye JC. Deep residual learning for accelerated MRI using magnitude and phase networks. IEEE Transactions on Biomedical Engineering. 2018;65(9):1985-95.
Quan TM, Nguyen-Duc T, Jeong WK. Compressed sensing MRI reconstruction using a generative adversarial network with a cyclic loss. IEEE Transactions on Medical Imaging. 2018;37(6):1488-97.
Zhu B, Liu JZ, Cauley SF, Rosen BR, Rosen MS. Image reconstruction by domain-transform manifold learning. Nature. 2018;555(7697):487-92.
Eo T, Jun Y, Kim T, Jang J, Lee HJ, Hwang D. KIKI-net: cross-domain convolutional neural networks for reconstructing undersampled magnetic resonance images. Magnetic Resonance in Medicine. 2018;80(5):2188-201.
Akçakaya M, Moeller S, Weingärtner S, Uğurbil K. Scan-specific robust artificial-neural-networks for k-space interpolation (RAKI) reconstruction: Database-free deep learning for fast imaging. Magnetic Resonance in Medicine. 2019;81(1):439-53.
Pezzotti N, Yousefi S, Elmahdy MS, Van Gemert JH, Schuelke C, Doneva M, Nielsen T, Kastryulin S, Lelieveldt BP, Van Osch MJ, De Weerdt E, et al. An adaptive intelligence algorithm for undersampled knee MRI reconstruction. IEEE Access. 2020;8:204825-38.
Hammernik K, Schlemper J, Qin C, Duan J, Summers RM, Rueckert D. Systematic evaluation of iterative deep neural networks for fast parallel MRI reconstruction with sensitivity-weighted coil combination. Magnetic Resonance in Medicine. 2021;86(4):1859-1872.
Knoll F, Murrell T, Sriram A, Yakubova N, Zbontar J, Rabbat M, Defazio A, Muckley MJ, Sodickson DK, Zitnick CL, Recht MP, et al. Advancing machine learning for MR image reconstruction with an open competition: Overview of the 2019 fastMRI challenge. Magnetic Resonance in Medicine. 2020;84(6):3054-70.
Muckley MJ, Riemenschneider B, Radmanesh A, Kim S, Jeong G, Ko J, Jun Y, Shin H, Hwang D, Mostapha M, Arberet S, et al. Results of the 2020 fastMRI challenge for machine learning MR image reconstruction. IEEE Transactions on Medical Imaging. 2021;40(9):2306-17.
Sriram A, Zbontar J, Murrell T, Defazio A, Zitnick CL, Yakubova N, Knoll F, Johnson P. End-to-end variational networks for accelerated MRI reconstruction. In MICCAI 2020 Oct 4 (pp. 64-73).
Huang G, Liu Z, Van Der Maaten L, Weinberger KQ. Densely connected convolutional networks. In CVPR 2017 (pp. 4700-4708).
Defazio A. Offset sampling improves deep learning based accelerated MRI reconstructions by exploiting symmetry. arXiv:1912.01101. 2019 Dec 2.
Defazio A, Tygert M, Ward R, and Zbontar J, Compressed sensing with a Jackknife, a Bootstrap, and Visualization. Journal of Data Science, Statistics, and Visualisation, to appear.
Ramani S, Liu Z, Rosen J, Nielsen JF, Fessler JA. Regularization parameter selection for nonlinear iterative image restoration and MRI reconstruction using GCV and SURE-based methods. IEEE Transactions on Image Processing. 2012;21(8):3659-72.
Edupuganti V, Mardani M, Vasanawala S, Pauly J. Uncertainty quantification in deep MRI reconstruction. IEEE Transactions on Medical Imaging. 2020;40(1):239-50.
Zbontar J, Knoll F, Sriram A, Murrell T, Huang Z, Muckley MJ, Defazio A, Stern R, Johnson P, Bruno M, Parente M, et al. fastMRI: An open dataset and benchmarks for accelerated MRI. arXiv:1811.08839. 2018.
Figures
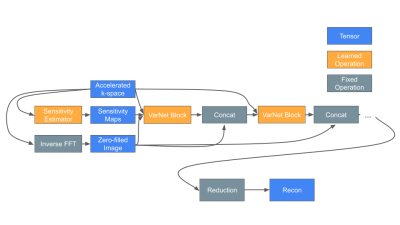
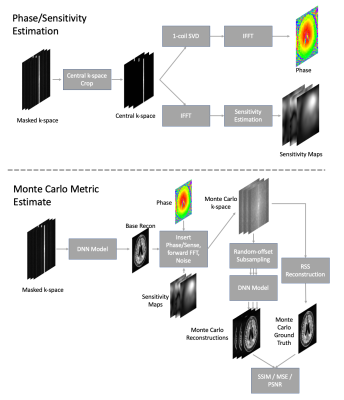
Figure 2: Diagram of Monte Carlo simulation pipeline. First, image phase and coil sensitivity maps are estimated from only the densely-sampled center region. Second, a simulated k-space is estimated by re-inserting phase into the DNN reconstruction, multiplying by sensitivity maps, applying the forward FFT, and adding noise. Multiple sampling patterns are applied and reconstructed. Monte Carlo metrics (SSIM or PSNR) are estimated using the original reconstruction as a ground truth.
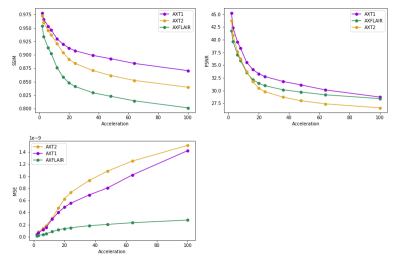
Figure 3: Volume distortion metrics across accelerations, separated by contrast type. T1 images are the easiest to reconstruct (according to metrics). Observable are the two regimes: the standard reconstruction regime below an acceleration of 20 and the super-resolution regime above an acceleration of 20. Image quality declines rapidly as fewer peripheral k-space lines are sampled and the rate of decline is higher in the first regime.
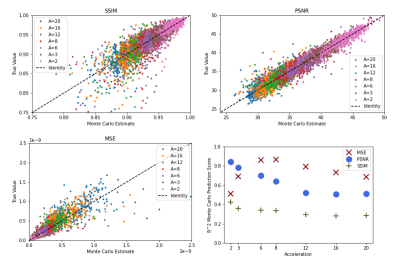
Figure 4: Monte Carlo results across acceleration factors (A=Acceleration). MC estimates were obtained by running 5 iterations of the procedure in Figure 2, followed by estimating scaling and offset parameters. The results in this figure are shown on hold-out test data. MSE estimates were calculated via the MC PSNR estimate. We also show R2 scores for the estimates at each acceleration as an indicator of prediction quality. According to R2 values, the PSNR and MSE predictions have the highest fidelity. We aggregate R2 values for each metric to simplify presentation.
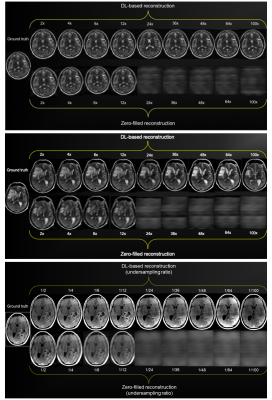
Figure 5: DL-based reconstructions in 3 illustrative cases (2 with pathology) at multiple undersampling schemes: (top) Normal healthy T2 image, (middle) T2-weighted pulse sequence in a patient with right frontal edema and mass effect, (bottom) T1-weighted post-contrast pulse sequence in a patient with a left heterogeneously enhancing, parieto-temporal lobe tumor. The quality of images with pathology decays considerably with the transition to the super-resolution regime. Four other pathology cases (not shown) had similar results.