Introduction

Like coil weighting in parallel imaging, nonlinear gradient encoding enables the sampled data to be interpreted as a weighted sum of adjacent k-space data points, making it helpful to fill in the trajectory gaps in k-space, especially when combined with coil sensitivity encoding in parallel imaging¹. Fast Rotary Nonlinear Spatial Acquisition (FRONSAC) is an imaging approach that applies a rapidly oscillating nonlinear gradient waveform during readout and has been shown to provide imaging acceleration while maintaining the reliability of a standard Cartesian acquisition^2,3. Previous work has demonstrated the feasibility of reconstructing FRONSAC data via iterations over the full encoding matrix, as well as by inversion of the PSF modulation seen in a transform of the data^4,5.

Previous work has shown that deep learning reconstruction can produce faster reconstruction with reduced noise and artifacts in both Cartesian and non-Cartesian trajectories, but these points have not been explored under nonlinear gradient encoding. In particular, FRONSAC typically requires a rigorous field mapping of the nonlinear gradient, so improved robustness against potential trajectory errors might lower this requirement.

Here we study the utility of reconstructing FRONSAC with MoDL, incorporating the FRONSAC encoding matrix in the MoDL reconstruction network⁶. We present studies of whether MoDL reconstruction suppresses noise, allows for greater undersampling, or improves robustness to errors in the nonlinear field mapping. To our knowledge, this is the first work using deep learning reconstruction for nonlinear gradient imaging.

Method

Model-based imaging schemes map and image x to the sensor domain data y using an encoding matrix A.
$$y=A(x)$$
In FRONSAC imaging, $$$A=P F Psf S$$$, where $$$P$$$ is the sampling operator, $$$F$$$ is the Fourier transform, $$$S$$$ is the multiplication with the sensitivities. $$$Psf$$$ is determined by nonlinear gradient channels and the corresponding phase trajectory.
$$Psf_{x,y,z}(\omega)=F^{-1}(exp(i2\pi P_{nlg}(x,y,z,t)))$$
We formulate the reconstruction of the image as an optimization problem consisting of data consistency term and regularization term $$x_{rec}=arg min||A(x)-y||_2^2+\lambda||(I-D_w)(x)||^2$$
where $$$D_w$$$ is the denoiser to remove alias artifacts and noise.

This problem can be solved as$$x_{n+1} = (A^HA+\lambda I)^{-1}(A^H(y)+\lambda D_w(x_n))$$
In many cases, the operator of $$$(A^HA+\lambda I)$$$ is not analytically invertible, so this problem often needs to be solved using a numerical optimization scheme.

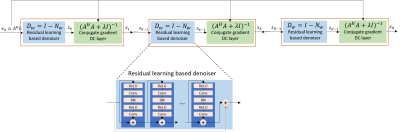
An unrolled recursive algorithm forms the deep learning network, MoDL-FRONSAC, as is shown in Figure 1. Each residual learning based denoiser block, which collects image information, consists of a 6-layer model with 64 filters at each layer. The following data consistency blocks enforce consistency with acquired data where conjugate gradient optimization is used instead of analytical inversion of $$$(A^HA+\lambda I)$$$. The model is unrolled assuming 4 iterations of the optimization problem. The training is end-to-end, and the loss function is the mean squared error between predicted images and ground truth.

The network was trained on retrospectively undersampled 2D brain magnetic resonance images selected from the Human Connectome Project (HCP)⁷. 100 images were divided into training, validation, and test dataset with a ratio of 3:1:1. Experimental sensitivity maps from an 8 channel coil and an experimentally measured FRONSAC trajectory⁵ were used in data simulation. The reconstruction implementation was based on the package Deepinpy⁸.

Different levels of Gaussian noise were added to the signal to study the effect of noise. At a fixed noise level, we also tested different undersampling factors, training a new denoiser for each case of undersampling. The results of MoDL-FRONSAC were compared to the PSF-based reconstruction method as well as conjugate gradient SENSE. To study the correction of errors in the nonlinear gradient trajectory, a single $$$D_w$$$ was trained with a range of FRONSAC gradient waveforms. For each test set, errors in the trajectory of the nonlinear gradient were simulated by scaling the FRONSAC gradient in the data generation step without making any changes in the reconstruction pipeline.

Results and Discussion

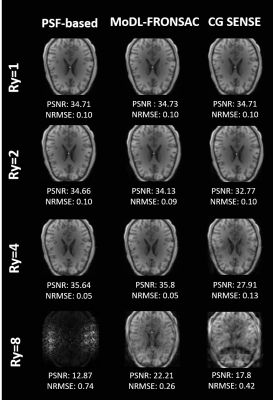
Figure 2 tabulates metrics across the test dataset for varying levels of signal noise. In this implementation, performance relative to Gaussian noise is fairly similar for PSF-based and MoDL reconstructions, which are both improvements on the CG-SENSE results.

Figure 3 shows results from the study of undersampling performance at a fixed noise level. Results are similar at modest undersampling factors. However, at R=8 the DL layer of MoDL appears to rescue the image and remove the most prominent aliasing artifacts, though some noise-like image degradation is still apparent.

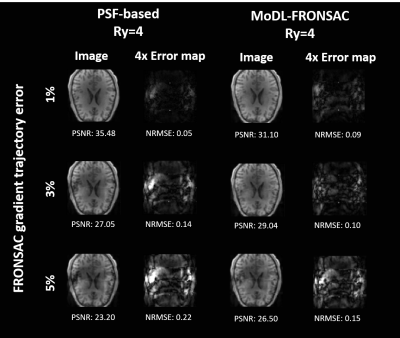
Finally, Figure 4 shows results simulating a scale factor between the FRONSAC gradient used to generate data and the FRONSAC gradient used in the reconstruction. While both reconstruction methods show some image degradation with increasing trajectory errors, NRMSE and PSNR are both better with MoDL reconstruction. Difference images also reveal a more distributed artifact, which may be amenable to additional regularization strategies.

Conclusion

This work demonstrates that MoDL reconstruction can improve images acquired with nonlinear encoding. The results show substantial improvements at high undersampling factors, and they also demonstrate that the denoising network can be trained to correct for artifacts arising from specific trajectory errors. This latter feature is particularly important as it may reduce mapping requirements for nonlinearly encoded imaging strategies.

Acknowledgements

The authors thank Kalina Slavkova and Jon Tamir for guidance, as well as NIH NIBIB Grant EB022030 for funding support.