Introduction

Truncation of high-frequency information above the maximum spatial frequency sampled during the Magnetic Resonance Imaging (MRI) experiment provokes spurious Gibbs Ringing (GR) next to tissue transitions. This may degrade the radiological quality of the images and confound segmentation algorithms, especially when using sinc interpolation. Classical solutions involve the application of a low pass filter to attenuate k-space discontinuities, but they introduce blurring. Recent works have explored spectral extrapolation¹ by deep learning, including self-supervised methods^2,3, knowledge transfer⁴, and combination with previous non-linear approaches⁵. However, these techniques are limited by availability of training data or transferability of results to different scales or sequences. The Deep Decoder⁶ (DD) has been introduced to solve inverse imaging problems without training, relaxing computational requirements of alternative approaches⁷, and offering competitive results with respect to training schemes in its application to MRI reconstruction⁸. Its functioning is based on implicitly biasing the reconstruction results towards the statistics of natural images, which could be particularly effective to circumvent GR.

Methods

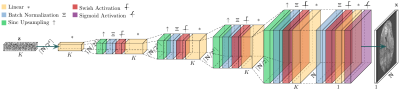
Image inversion based on the DD generative model is achieved by:$$\hat{\boldsymbol{\theta}}=\displaystyle\mbox{argmin}_{\boldsymbol{\theta}}\|\mathbf{M}\mathbf{A}\boldsymbol{\mathcal{G}}_\boldsymbol{\theta}(\mathbf{z})-\mathbf{y}\|_2^2\,\,\mbox{with}\,\,\hat{\mathbf{x}}=\boldsymbol{\mathcal{G}}_\hat{\boldsymbol{\theta}}(\mathbf{z})$$with $$$\mathbf{M}$$$ a mask indicating the acquired k-space samples, $$$\mathbf{A}$$$ a forward model matrix, $$$\boldsymbol{\mathcal{G}}$$$ the DD generator, $$$\mathbf{z}$$$ a fixed random input vector, $$$\boldsymbol{\theta}$$$ the parameters of the network, to be fitted by backpropagation, $$$\mathbf{y}$$$ the padded observations, and $$$\mathbf{x}$$$ the reconstruction, obtained by propagating $$$\mathbf{z}$$$ through $$$\boldsymbol{\mathcal{G}}$$$ using the fitted parameters $$$\hat{\boldsymbol{\theta}}$$$. We study two models for $$$\mathbf{A}$$$:$$\mathbf{A}=\mathbf{F},$$with $$$\mathbf{F}$$$ the Fourier transform of the image, used for GR correction from magnitude images, and$$\mathbf{A}=\mathbf{F}\mathbf{O}\mathbf{S},$$with $$$\mathbf{O}$$$ a spatial overlap matrix from uniformly subsampled k-space, and $$$\mathbf{S}$$$ a coil sensitivity matrix, used for direct spectral extrapolation of complex reconstructions from accelerated k-space data in parallel imaging. Results are provided for 2D reconstructions.
The original DD architecture has been modified for improved performance⁹ (Fig. 1). In our experiments, we use $$$L=\mbox{ceil}(\mbox{log}_2\sqrt{N_1N_2})-3$$$ DD scales with $$$N_1$$$ and $$$N_2$$$ the target grid sizes for $$$\mathbf{x}$$$, a $$$N_{\theta}\simeq N_1N_2$$$ parameter network, and the Adam optimizer with $$$20000$$$ iterations.
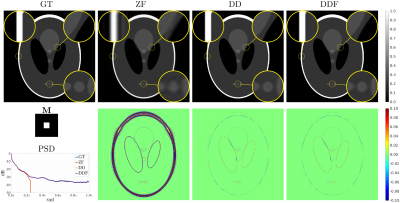
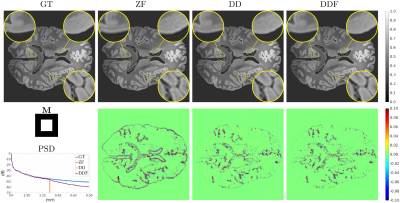
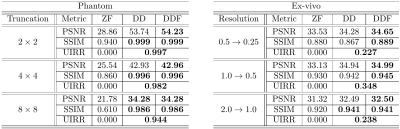
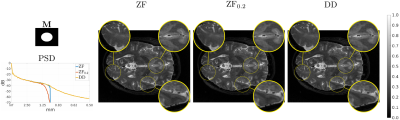
The modified Shepp-Logan phantom of size $$$512\times 512$$$ is used as Ground Truth (GT) for in-silico validation of GR correction when truncating the original spectrum to $$$1/8$$$, $$$1/4$$$, and $$$1/2$$$ the original sizes for both axes. A publicly available $$$0.1\,\mbox{mm}$$$ resolution ex-vivo scan of a human brain¹⁰ is used to study the GR problem for truncation at $$$0.5\,\mbox{mm}$$$, $$$1\,\mbox{mm}$$$ and $$$2\,\mbox{mm}$$$ by comparing reconstructions of an axial slice with GT datasets downsampled to twice the corresponding truncation frequencies. Peak Signal to Noise Ratio (PSNR), Structural Similarity Index Measure¹¹ (SSIM) and a specific metric termed Unsampled Information Retrieval Ratio (UIRR):$$\text{UIRR}=1-\frac{\|(\mathbf{I}-\mathbf{M})\mathbf{F}(\hat{\mathbf{x}}-\mathbf{x}^{\ast})\|_2^2}{\|(\mathbf{I}-\mathbf{M})\mathbf{F}\mathbf{x}^{\ast}\|_2^2},$$ with $$$\mathbf{I}$$$ the identity matrix and $$$\mathbf{x}^{\ast}$$$ the GT, are computed for both experiments. In all cases we compare the DD generative fit, Zero-Filled (ZF) images, and DD for Filling (DDF) the unsampled areas of the spectrum only. Finally, a volumetric Cartesian TSE brain sequence acquired on a consented volunteer using a Philips $$$3\,\mbox{T}$$$ Achieva scanner ($$$1\,\mbox{mm}$$$ isotropic resolution, $$$240\times 188\times 240\,\mbox{mm}$$$ IS-LR-AP field of view, $$$1.4\times 1.4$$$ acceleration, elliptical shutter, repetition time $$$T_{\text{R}}=2.5\,\mbox{s}$$$, and echo time $$$T_{\text{E}}=254.3\,\mbox{ms}$$$) is used to test the complex integrated formulation. Namely, parallel imaging generative reconstruction onto a $$$0.5\,\mbox{mm}$$$ pixel size image at the center of the IS readout direction is compared to standard ZF SENSitivity Encoded (SENSE) reconstruction without and with GR mitigation based on a Tukey filter (taper ratio $$$0.2$$$, ZF_$$$0.2$$$).

Results

Fig. 2 (results for $$$1/4$$$ truncation) shows noticeable reduction of GR oscillations when comparing DD or DDF to ZF. Moreover, visual results and Power Spectral Density (PSD) plots averaged along the two image axes suggest prominent retrieval of Unsampled High Frequency (UHF) components for this piecewise continuous phantom. Visual improvement in GR suppression and contrast when using the DD is observed in the ex-vivo experiment in Fig. 3 (results for $$$1\,\mbox{mm}$$$ truncation), but in this case richer UHF information is only partially retrieved. As reported in Fig. 4, DD reconstructions provide improved PSNR and UIRR over ZF for all compared configurations, with improvements in SSIM at $$$0.25\,\mbox{mm}$$$ GT resolution observed only for the DDF strategy. Moreover, UIRR approaches $$$1$$$ for the phantom and is noticeably higher than $$$0$$$ for brain data. Reconstructions in Fig. 5 show ringing effects for ZF-SENSE, which are reduced for ZF_$$$0.2$$$-SENSE at the price of blurred structures. The DD reconstruction provides a better trade-off with minor ringing and sharp definition of fine detailed structures.

Discussion

We have presented a deep generator based method for unsupervised GR correction that can be used as a post-processing step or integrated into classical reconstruction formulations. Results show effective correction of GR artifacts with partial retrieval of UHF components in a variety of scales and truncation factors. Comparisons with supervised methods and tests on partial Fourier reconstruction or different acquisition encodings remain to be performed. For application to 3D data we plan to study decomposition into patches and convergence acceleration to alleviate memory and run time requirements. These refinements are also expected to improve the DD fit for large grid sizes.

Conclusion

Unsupervised GR correction can be achieved with generative deep architectures, either as a post-processing step or by integration into the reconstruction, with flexible applicability at different scales or to different sequences.

Acknowledgements

This work is funded by the Ministry of Science and Innovation, Spain, under the Beatriz Galindo Programme [BGP18/00178]. This work has been supported by the Madrid Government (Comunidad de Madrid-Spain) under the Multiannual Agreement with Universidad Politécnica de Madrid in the line Support for R&D projects for Beatriz Galindo researchers, in the context of the V PRICIT (Regional Programme of Research and Technological Innovation).