0845
Parallel Greedy Learning for Accelerating Cardiac Cine MRI1Electrical Engineering, Stanford University, Stanford, CA, United States, 2Radiology, Stanford University, Stanford, CA, United States
Synopsis
Deep unrolled models have recently shown state-of-the-art performance for reconstruction of dynamic MR images. However, training these networks via backpropagation is limited by intensive memory and compute requirements to calculate gradients and store intermediate activations per layer. Motivated by these challenges, we propose an alternative training method by greedily relaxing the training objective. Our approach splits the end-to-end network into decoupled network modules, and optimizes each module separately, avoiding the need to compute end-to-end gradients. We demonstrate that our method outperforms end-to-end backpropagation by 3.3 dB in PSNR and 0.025 in SSIM with the same memory footprint.
Introduction
Deep unrolled models have recently surpassed parallel imaging1 and compressed sensing2 for reconstruction of undersampled dynamic MR images3,4 .These methods alternate between data-consistency and a neural network with 3D convolutions5 . However, end-to-end training of deep unrolled networks for dynamic MRI is constrained by GPU memory due to high memory costs and computational complexity of 3D convolutional neural networks (CNNs). Therefore, memory-efficient training techniques are crucial for applying deep unrolled networks to high-dimensional imaging applications6 such as cardiac cine and phase-contrast imaging, among many others.Previous methods tackle this issue by modifying the deep unrolled network to incorporate a stochastic approximation of data-consistency7, or by modifying the network to instead solve for the data in a compact subspace8. Another line of work uses reverse recalculations to obviate the need to store intermediate activations, with an expense of higher computation time9,10.
In this work, we propose an alternative training method for deep unrolled networks termed greedy learning. We split the end-to-end network into decoupled network modules, and optimize each network module separately, thereby avoiding the need to compute and store end-to-end gradients. The proposed method is memory-efficient, enabling 3x more learnable network parameters on the same hardware. Furthermore, our method is applicable to any deep unrolled network, and can be synergistically combined with other memory-efficient approaches to further reduce memory consumption.
Theory
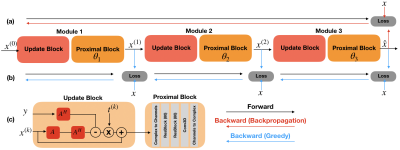
An alternative to backpropagation for training CNNs is greedy learning11. Here, we adapt greedy learning to deep unrolled networks. In this setup, deep networks are split into several shallow network modules, and gradient updates for each module are decoupled.When a mini-batch is sampled during training, the first module computes the forward pass on the mini-batch of images, performs a gradient update based on its own local loss, and passes the result of the forward pass to the next module. This procedure is repeated until the final module which produces the prediction of the network. Therefore, individual updates of each set of parameters are performed independently across different modules, which drastically reduces the memory requirement (Fig. 1).
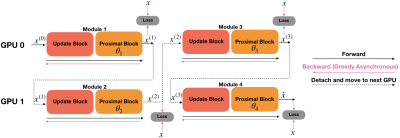
In addition, since individual updates of modules are independent, optimization of each module can be parallelized. In parallel greedy learning, the network modules are split across multiple devices. When a mini-batch is sampled, forward pass is computed sequentially through all modules. After forward pass is computed, each backward pass can be asynchronously executed among all modules in parallel. Since backward time is a primary bottleneck, asynchronous execution of the backward operation can greatly decrease overall computation time (Fig. 2).
Methods
We adopt the fully-sampled balanced SSFP 2D cardiac cine dataset used in12 for evaluation. 10 subjects are used for training, 2 subjects are used for validation, and 9 for testing. Training scans are split slice-by-slice to create 79 unique cine slices where each scan has 20 temporal frames. The matrix size for each scan varied within a range from 144x200 to 200x224. Scans are retrospectively undersampled using a k-t variable-density mask at 16x acceleration. We evaluate image quality using slice-based PSNR, SSIM and nRMSE.Training is performed in PyTorch13 on a Geforce RTX 2080 GPU (11GB). Networks are trained with the Adam optimizer14 for 200 epochs.
We compare greedy learning with backpropagation on the same hardware, using networks that occupy the maximum amount of available GPU memory with a batch size of 1. We adapt the network architecture from12 (Fig.1c). For both methods, each proximal block consisted of 2 residual blocks with 80 channels. For backpropagation, the network has 4 unrolled iterations, whereas for greedy learning the network has 12 unrolled iterations, where the network is split to 3 individual modules for training.
In addition, to benchmark forward and backward computation time, we fix the network architecture, and compare the computation time of backpropagation, greedy learning, and parallel greedy learning on 2 GPUs. The network used for benchmarking time has 4 unrolled iterations.
Results
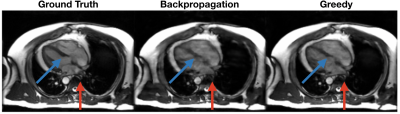
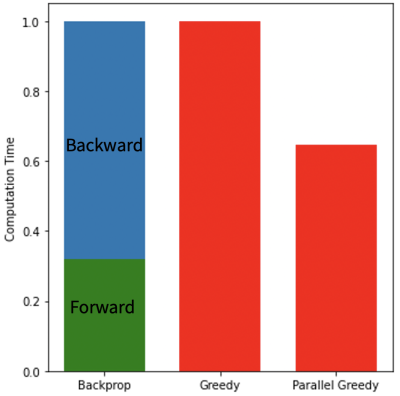
The greedy learning approach allowed for training a network with 3x as many unrolled iterations as backpropagation. As a result, the network trained with greedy learning outperformed the network trained with backpropagation by +3.3 dB PSNR, +0.025 SSIM and +0.029 nRMSE (Fig. 3) with the same memory footprint. Representative slices from the test set are shown in Fig. 4. Greedy learning improves reconstruction fidelity compared to backpropagation, successfully mitigating aliasing artifacts and recovering fine anatomical structures.Compute time comparison for backpropagation, greedy learning, and parallel greedy learning are illustrated in Fig. 5. Split across two devices, parallel greedy learning results in at least a 1.5x speed up in training compared to backpropagation and greedy learning.
Discussion and Conclusion
We found that while greedy learning does not calculate end-to-end gradients via backpropagation, it achieves exceptional generalization performance on test data. In addition, greedy learning enables training larger models for cardiac cine. While training time might increase as model size increases, parallel greedy learning can speed up training to enable a feasible training time.We presented parallel greedy learning for accelerating cardiac cine MRI. Parallel greedy learning allows for 3x more learnable network parameters compared to backpropagation with the same memory footprint, which improves reconstruction performance for cardiac cine images.
Acknowledgements
This work was supported by NIH Grants R01 EB009690, R01 EB026136 and NSF Grant DGE-1656518.References
1. M. Murphy, M. Alley, J. Demmel, K. Keutzer, S. Vasanawala, and M. Lustig. Fast ℓ1-SPIRiT compressed sensing parallel imaging MRI: Scalable parallel implementation and clinically feasible runtime. IEEE Trans Med Imaging. 2012;31(6):1250-1262. doi:10.1109/TMI.2012.2188039
2. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58(6):1182-1195. doi:10.1002/mrm.21391
3. Qin C, Schlemper J, Caballero J, Price AN, Hajnal JV, Rueckert D. Convolutional recurrent neural networks for dynamic MR image reconstruction. IEEE Trans Med Imaging. 2019;38(1):280–290. doi:10.1109/TMI.2018.2863670
4. Biswas S, Aggarwal HK, Jacob M. Dynamic MRI using model-based deep learning and SToRM priors: MoDL-SToRM. Magn Reson Med. 2019;82(1):485-494. doi:10.1002/mrm.27706
5. Schlemper J, Caballero J, Hajnal JV, Price A, Rueckert D. A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans Med Imaging. 2018;37(2):491–503. doi:10.1007/978-3-319-59050-9_51
6. Ong F, Zhu X, Cheng JY, et al. Extreme MRI: Large-Scale Volumetric Dynamic Imaging from Continuous Non-Gated Acquisitions. ArXiv:1909.13482 Phys. September 2019. http://arxiv.org/abs/1909.13482.
7. Liu, J., Sun, Y., Gan, W., Xu, X., Wohlberg, B., & Kamilov, U. S. (2021). Sgd-net: Efficient model-based deep learning with theoretical guarantees. IEEE Transactions on Computational Imaging.
8. Sandino, C. M., Ong, F., Iyer, S. S., Bush, A., & Vasanawala, S. (2021, October). Deep subspace learning for efficient reconstruction of spatiotemporal imaging data. In NeurIPS 2021 Workshop on Deep Learning and Inverse Problems.
9. Kellman, M., Zhang, K., Markley, E., Tamir, J., Bostan, E., Lustig, M., & Waller, L. (2020). Memory-efficient learning for large-scale computational imaging. IEEE Transactions on Computational Imaging, 6, 1403-1414.
10. Wang, K., Kellman, M., Sandino, C. M., Zhang, K., Vasanawala, S. S., Tamir, J. I., ... & Lustig, M. (2021). Memory-efficient Learning for High-Dimensional MRI Reconstruction. arXiv preprint arXiv:2103.04003.
11. Belilovsky, E., Eickenberg, M., & Oyallon, E. (2020, November). Decoupled greedy learning of cnns. In International Conference on Machine Learning (pp. 736-745). PMLR.
12. Sandino, C. M., Lai, P., Vasanawala, S. S., & Cheng, J. Y. (2021). Accelerating cardiac cine MRI using a deep learning‐based ESPIRiT reconstruction. Magnetic Resonance in Medicine, 85(1), 152-167.
13. Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., ... & Chintala, S. (2019). Pytorch: An imperative style, high-performance deep learning library. Advances in neural information processing systems, 32, 8026-8037.
14. Kingma DP, Ba JL. Adam: A method for stochastic gradient descent. In: Proceedings of the 3rd International Conference on Learning Representations. San Diego, CA, United States; 2015.
Figures