0844

Deep Plug-and-Play multi-coil compressed sensing MRI with matched aliasing: the Denoising-P-VDAMP algorithm

Charles Millard¹, Aaron Hess¹, Boris Mailhe², and Jared Tanner³
¹Wellcome Centre for Integrative Neuroimaging, FMRIB, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom, ²Siemens, Princeton, NJ, United States, ³Mathematical Institute, University of Oxford, Oxford, United Kingdom

Synopsis

We present the Denoising Parallel Variable Density Approximate Message Passing (D-P-VDAMP) algorithm for multi-coil compressed sensing MRI with a learned prior. To our knowledge, D-P-VDAMP is the first Plug-and-Play method for multi-coil k-space data where the distribution of the training data's aliasing matches the actual distribution seen during reconstruction. We evaluate the performance of the proposed method on the fastMRI knee dataset and find substantial improvements in reconstruction quality compared with Plug-and-Play FISTA with the same network architecture in similar training and reconstruction time.

Introduction

In recent years there has been considerable research attention on reconstructing accelerated k-space acquisitions with learned priors. Numerous approaches have been suggested, including direct data-to-image networks^1,2 and networks formed by unrolling compressed sensing ^3-6. This abstract focusses on deep Plug-and-Play (P&P) methods ^7-9, which replace the usual prior-based step of a reconstruction algorithm with a learned "denoiser".

The denoiser of deep P&P algorithms are typically trained on data simulated by corrupting reference images with zero-mean white complex Gaussian noise ^8,9. Although sampling k-space incoherently leads to "noise-like" aliasing of the intermediate image estimate, a zero-mean white complex Gaussian distribution poorly models its distribution in general. This is a key shortcoming of existing P&P methods for MRI: there is a substantial mismatch between the distribution of the aliasing of the training data and the actual aliasing when the denoiser is used as part of a reconstruction algorithm.

The authors recently proposed the Parallel Variable Density Approximate Message Passing (P-VDAMP) algorithm ^10,11. To our knowledge, P-VDAMP is the first algorithm for randomly sampled multi-coil k-space data where the distribution of the aliasing of the intermediate estimate is approximately known. Specifically, for Bernoulli sampled k-space data the intermediate estimate of P-VDAMP $$$\hat{\textbf{x}}_k$$$ at iteration $$$k$$$ obeys $$\hat{\textbf{x}}_k{\approx}\textbf{x}_0+\mathcal{CN}(\textbf{0},\mathbf{\Sigma}_k^2),$$ where $$$\textbf{x}_0$$$ is the ground-truth image and $$$\mathcal{CN}(\textbf{0},\mathbf{\Sigma}_k^2)$$$ is complex Gaussian noise with independent real and imaginary parts with zero mean and covariance matrix $$$\mathbf{\Sigma}_k^2$$$. P-VDAMP's $$$\mathbf{\Sigma}_k^2$$$ can be accurately modelled as diagonal in the wavelet domain, so that $$$\mathbf{\Sigma}_k^2{\approx}\mathbf{\Psi}\mathrm{Diag}(\pmb{\tau}_k)\mathbf{\Psi}^T$$$ for vector $$$\pmb{\tau}_k$$$ and orthogonal wavelet transform $$$\mathbf{\Psi}$$$. Eqn. (1) is known as P-VDAMP's "state evolution", since the algorithm's "state" at iteration $$$k$$$ can be fully characterised by $$$\mathbf{\Sigma}_k^2$$$. This abstract presents Denoising-P-VDAMP, a P&P version of P-VDAMP that leverages state evolution to ensure that the aliasing of the training data matches the distribution of the aliasing during reconstruction ¹², building on previous work by other authors on Denoising-AMP ^13,14 and single-coil Denoising-VDAMP ¹⁵.

Method

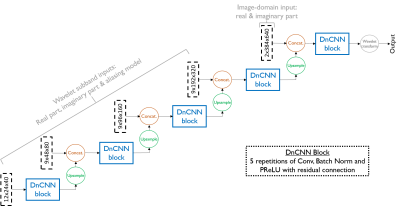
Since P-VDAMP's aliasing is modelled in the wavelet domain, we propose a denoising architecture based on Denoising CNN (DnCNN) ¹⁶ that takes wavelet coefficients and the corresponding aliasing model as its input. The proposed network architecture, which we term Wavelet-DnCNN (W-DnCNN), is represented in Fig. 1. The wavelet coefficients are concatenated with their corresponding aliasing model and inputted to the network scale-by-scale, starting with the coarsest and passing through a DnCNN-based block at every scale.

We evaluated the the proposed method on multi-coil knee data from the fastMRI dataset ¹⁷. To prepare the raw k-space data for training, we Bernoulli sampled k-space with an sampling ratio generated uniformly at random between $$$0.05$$$ and $$$0.5$$$, estimated the sensitivity maps with ESPIRiT ¹⁸, and computed the fully sampled wavelet coefficients and aliasing model estimate $$$\pmb{\tau}_j$$$. We simulated the $$$i$$$th aliased training point $$$\mathbf{r}_i$$$ by corrupting ground-truth wavelet coefficients $$$\mathbf{w}_{0,i}$$$ with Gaussian noise,$$\mathbf{r}_i=\mathbf{w}_{0,i}+\mathcal{CN}(\mathbf{0},\text{Diag}(\pmb{\tau}_{j})),$$ where $$$j$$$ was shuffled with $$$i$$$ once per epoch.

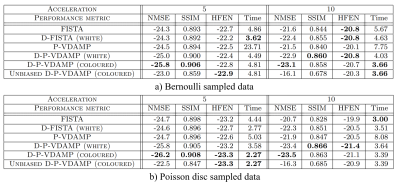
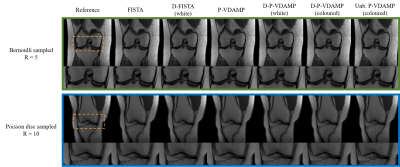
For comparative non-learned reconstructions, we ran SURE-optimal soft thresholding P-VDAMP algorithm ¹¹ and FISTA ¹⁹. For a comparative deep P&P method, we ran D-FISTA ²⁰. We used the same W-DnCNN architecture as D-P-VDAMP for D-FISTA but trained on white Gaussian noise, as in previous implementations of P&P for MRI ^8,9. We ran D-P-VDAMP with both the coloured and white denoiser. As well as the usual, biased output of P-VDAMP ¹¹, we also evaluated the reconstruction quality of the intermediate estimate that obeys state evolution, $$$\hat{\mathbf{x}}_k$$$, referred to as "Unbiased" D-P-VDAMP, which we found generated sharper-looking images at the cost of higher Mean-Squared-Error (MSE). We ran all algorithms on Bernoulli and Poisson disc sampled data at acceleration factors $$$R=5,10$$$, as shown in Fig. 2.

Results and discussion

Fig. 3 shows the average Normalised MSE (NMSE), Structural Similarity Index (SSIM), High-Frequency Error Norm (HFEN) ²¹ and time to convergence on the test set. Coloured D-P-VDAMP's NMSE, SSIM and HFEN were consistently better than D-FISTA, illustrating the advantage of training on matched aliasing. D-P-VDAMP's required number of iterations to convergence was substantially smaller, leading to a faster average time to convergence than D-FISTA in 3 out of 4 test settings despite requiring around $$$3$$$ times longer per iteration.

Two reconstruction examples for randomly selected slices from the test set are shown in Fig. 4 for Bernoulli at $$$R=5$$$ and Poisson disc at $$$R=10$$$. Unbiased D-P-VDAMP qualitatively retains fine anatomical detail well despite a relatively poor NMSE. An interpolation between the unbiased and biased outputs could be considered in the future to adjust the perception/distortion trade-off ²² without requiring adversarial penalisation.

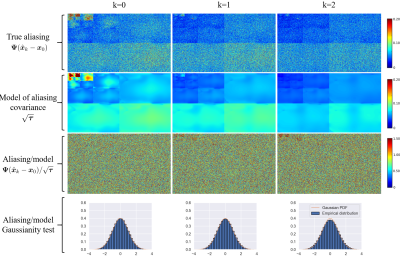
Evidence for D-P-VDAMP's approximate state evolution for the Bernoulli sampled example from Fig. 4 is shown in Fig. 5. Since P-VDAMP's aliasing model is not specifically constructed for Poisson disc sampled data, its aliasing is not as accurately modelled by $$$\pmb{\tau}$$$. Nonetheless, Fig. 3 illustrates that the coloured aliasing model still offers an advantage over the less accurate white model.

Conclusions

D-P-VDAMP's state evolution provides a way to train a denoising CNN on simulated aliasing that closely matches the actual aliasing seen during reconstruction. D-P-VDAMP with a coloured denoiser outperformed D-FISTA's average NMSE, SSIM and HFEN in a comparable time to convergence.

Acknowledgements

This work was supported in part by an EPSRC Industrial CASE studentship with Siemens Healthineers, voucher number 17000051, and in part by The Alan Turing Institute under EPSRC under Grant EP/N510129/1.

The concepts and information presented in this abstract are based on research results that are not commercially available. Future availability cannot be guaranteed.

References

1. Y. Yang, J. Sun, H. Li, and Z. Xu, “Deep ADMM-Net for compressive sensing MRI,” in Proceedings of the 30th international conference on neural information processing systems, pp. 10–18, 2016.

2. K. Hammernik, T. Klatzer, E. Kobler, M. P. Recht, D. K. Sodickson, T. Pock, and F. Knoll, “Learning a variational network for reconstruction of accelerated MRI data,” Magnetic Resonance in Medicine, vol. 79, no. 6, pp. 3055–3071, 2018.

3. S. Wang, Z. Su, L. Ying, X. Peng, S. Zhu, F. Liang, D. Feng, and D. Liang, “Accelerating magnetic resonance imaging via deep learning,” in 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI), pp. 514–517, IEEE, 2016.

4. B. Zhu, J. Z. Liu, S. F. Cauley, B. R. Rosen, and M. S. Rosen, “Image reconstruction by domain-transform manifold learning,” Nature, vol. 555, no. 7697, pp. 487–492, 2018.

5. T. M. Quan, T. Nguyen-Duc, and W.-K. Jeong, “Compressed sensing MRI reconstruction using a generative adversarial network with a cyclic loss,” IEEE transactions on medical imaging, vol. 37, no. 6, pp. 1488–1497, 2018.

6. M. Mardani, E. Gong, J. Y. Cheng, S. S. Vasanawala, G. Zaharchuk, L. Xing, and J. M.Pauly, “Deep generative adversarial neural networks for compressive sensing MRI,” IEEE transactions on medical imaging, vol. 38, no. 1, pp. 167–179, 2018.

7. S. V. Venkatakrishnan, C. A. Bouman, and B. Wohlberg, “Plug-and-play priors for model based reconstruction,” in 2013 IEEE Global Conference on Signal and Information Processing, pp. 945–948, 2013.

8. R. Ahmad, C. A. Bouman, G. T. Buzzard, S. Chan, S. Liu, E. T. Reehorst, and P. Schniter, “Plug-and-play methods for magnetic resonance imaging: Using denoisers for image recovery,” IEEE Signal Processing Magazine, vol. 37, pp. 105–116, 2020.

9. A. P. Yazdanpanah, O. Afacan, and S. Warfield, “Deep plug-and-play prior for parallel MRI reconstruction,” in 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), pp. 3952–3958, IEEE, 2019.

10. C. Millard, A. T. Hess, B. Mailhe, and J. Tanner, “Approximate message passing with a colored aliasing model for variable density Fourier sampled images,” IEEE Open Journal of Signal Processing, p. 1, 2020.

11. C. Millard, A. T. Hess, B. Mailhe, and J. Tanner, “Near-optimal tuning-free multi-coil compressed sensing MRI with Parallel Variable Density Approximate Message Passing,” in 2021 ISMRM annual meeting, 2021.

12. S. K. Shastri, R. Ahmad, C. Metzler, and P. Schniter, “Matching plug-and-play algorithms to the denoiser,” in NeurIPS 2021 Workshop on Deep Learning and Inverse Problems, 2021.

13. C. A. Metzler, A. Maleki, and R. G. Baraniuk, “From denoising to compressed sensing,” IEEE Transactions on Information Theory, vol. 62, no. 9, pp. 5117–5144, 2016.

14. C. Metzler, A. Mousavi, and R. Baraniuk, “Learned D-AMP: Principled neural network based compressive image recovery,” in Advances in Neural Information Processing Systems, pp. 1772–1783, 2017.

15. C. A. Metzler and G. Wetzstein, “D-VDAMP: Denoising-based approximate message passing for compressive MRI,” arXiv:2010.13211, 2020.

16. K. Zhang, W. Zuo, Y. Chen, D. Meng, and L. Zhang, “Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising,” IEEE Transactions on Image Processing, vol. 26, pp. 3142–3155, 2017.

17. J. Zbontar, F. Knoll, A. Sriram, T. Murrell, Z. Huang, M. J. Muckley, A. Defazio,R. Stern, P. Johnson, M. Bruno, and Others, “fastMRI: An open dataset and bench-marks for accelerated MRI,” arXiv preprint arXiv:1811.08839, 2018.

18. M. Uecker, P. Lai, M. J. Murphy, P. Virtue, M. Elad, J. M. Pauly, S. S. Vasanawala, and M. Lustig, “ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA,” Magnetic Resonance in Medicine, vol. 71, pp. 990–1001, 2014.

19. A. Beck and M. Teboulle, “Fast iterative shrinkage-thresholding algorithm for linear inverse problems,” SIAM Journal on Imaging Sciences, vol. 2, pp. 183–202, 2009.

20. U. S. Kamilov, H. Mansour, and B. Wohlberg, “A plug-and-play priors approach for solving nonlinear imaging inverse problems,” IEEE Signal Processing Letters, vol. 24,no. 12, pp. 1872–1876, 2017.

21. S. Ravishankar and Y. Bresler, “MR image reconstruction from highly undersampled k-space data by dictionary learning,” IEEE transactions on medical imaging, vol. 30,no. 5, pp. 1028–1041, 2010.

22. Y. Blau and T. Michaeli, “The perception-distortion tradeoff,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 6228–6237, 2018.

Figures

Fig. 1. The proposed denoiser W-DnCNN for a 384x640 input with 4 decomposition scales. Black dashed boxes represent network inputs, which consist of a concatenation of the real part, imaginary part, and $$$\sqrt{\pmb{\tau}}$$$ at each wavelet scale, or for the top-right input the real and imaginary parts of the image-domain pixels. The blue rectangles, "DnCNN Blocks'', contain all the trainable parameters. The green circles are fixed bilinear upsampling layers, which scale the dimension of the channels by 2, so that they match the dimension of the subbands at the next-coarsest scale.

Fig. 2. An example of the probability density scheme and Bernoulli and Poisson disc masks for $$$R = 10$$$ sampling.

Fig. 3. Average performance of algorithms on the test set for Bernoulli and Poisson disc sampled data for acceleration factors $$$R = 10$$$ and $$$R = 5$$$. Here, NMSE and HFEN are in decibels and time is in seconds. The best performances are highlighted in bold.

Fig. 4. Example reconstructions from the $$$R = 5$$$ Bernoulli sampled and $$$R = 10$$$ Poisson Disc sampled experiments.

Fig. 5. The wavelet-domain aliasing of the intermediate estimate of D-P-VDAMP and its covariance model $$$\sqrt{\pmb{\tau}}$$$ for iterations $$$k = 0, 1, 2$$$. Here, the symbol "/" refers to entry-wise division. The third and fourth row are evidence that $$$\hat{\mathbf{x}}_k \approx \mathbf{x}_0 + \mathcal{CN}(\mathbf{0}, \mathbf{\Psi} \text{Diag}(\pmb{\tau})\mathbf{\Psi}^T)$$$ approximately holds; D-P-VDAMP obeys a state evolution.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

0844

DOI: https://doi.org/10.58530/2022/0844