Introduction

The ability to obtain images with different types of tissue contrast is a major advantage of using MRI. Routine clinical MR protocols include at least three different tissue contrasts (T1-weighted, T2-weighted and FLAIR). The total scan time is usually more than 20 minutes. It can be challenging for patients to stay still for the entire MR scan, and motion artifacts can render images useless for diagnosis. Several studies have used neural networks to generate synthetic MR images and contrast conversion with image-to-image translation^1,2. However, synthesizing tissue contrasts without taking account into MR physics models might be susceptible to the blurring and artifacts. In this study, to tackle the aforementioned challenges, we propose a physics-constrained network that first generates parameter maps (quantitative T1, T2, and M0) from an acquired T1-weighted image and then contrains synthesis of the clinical contrasts such as T2-weighted and FLAIR with Bloch equations. To demonstrate the usefulness of the proposed method, we conduct synthesis of missing tissue constrasts from clinical MR scans of healthy controls and Multiple Sclerosis (MS) patients.

Methods

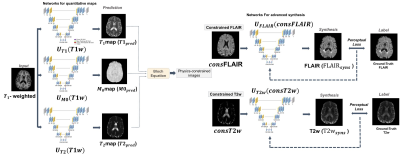
Pipeline
Figure 1 describes the proposed physics-contrained synthesis network. Given a T1-weighted image, we predict T1, T2, and M0 parameter maps using the pre-trained U-Nets³.$$T1_{pred}=U_{T1}(T1w), \quad T2_{pred}=U_{T2}(T1w), \quad M0_{pred}=U_{M0}(T1w) \quad (Eq. 1)$$
We then generate physics-contrained T2-weighted and FLAIR images by applying predicted parameter maps to Bloch equations as following.$$consT2=M0_{pred}\times(1-e^{-\frac{TR}{T1_{pred}}})\times(e^{-\frac{TE}{T2_{pred}}}) \quad (Eq. 2)$$$$consFLAIR=M0_{pred}\times(1-2\times e^{-\frac{TI}{T1_{pred}}}+e^{-\frac{TR}{T1_{pred}}})\times(e^{-\frac{TE}{T2_{pred}}}) \quad (Eq. 3)$$
Where TR, TE and TI are repitation time, echo time and inversion time, respectively. We then feed physic-constrained images to separate U-Nets to synthesize T2-weighted and FLAIR images.$$T2w_{syns}=U_{T2w}(consT2w) \quad (Eq. 4)$$$$FLAIR_{syns}=U_{FLAIR}(consFLAIR) \quad (Eq. 5)$$

Implementation details
We used perceptual loss function⁴ and ADAM optimizer for training our network, and the learning rate was 0.0001 and epochs was 50. For Eq. 2, we set TR=4800ms and TE=35ms. For Eq. 3, we set TR=6500ms, TE=5ms and TI=2000ms. All networks were trained with 5-fold cross-validation.

Dataset
All the data used to train networks were collected from 32 healthy controls and 5 MS patients who gave informed consent under an IRB-approved protocol. Imaging was performed on a 3T (Siemens).
When training networks to predict parameter maps, the dataset was composed of T1-weighted and ground-truth T1 maps acquired from the MP2RAGE ⁵. For ground truth T2-maps, multi-echo 3D GRASE sequence was used. The multi-echo data were processed using a nonnegative least-square fitting. Ground-truth M0 maps were estimated using a signal equation of INV2 images from the MP2RAGE sequence together with T1-map and T2-map.
When training networks $$$U_{T2w}$$$, $$$U_{FLAIR}$$$, input dataset was calculated by applying ground-truth parameter maps to Bloch equation 2 and 3. T2-weighted from GRASE images (17th echo) and FLAIR acquired from SPACE sequence⁶ were used as the labeled dataset.

Evaluation
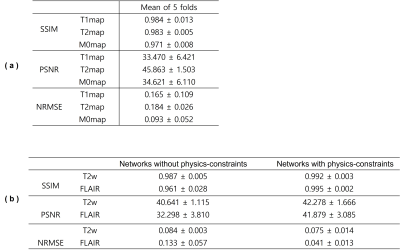
For comparison, we trained U-Nets to directly synthesize T2w from T1w and FLAIR from T1w. We evaluate the synthesis quality by measuring mean values of SSIM, PSNR and NRMSE from 5-fold cross-validation.

Results

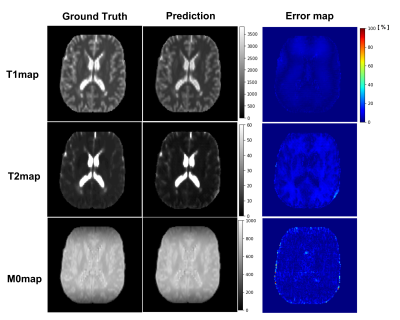
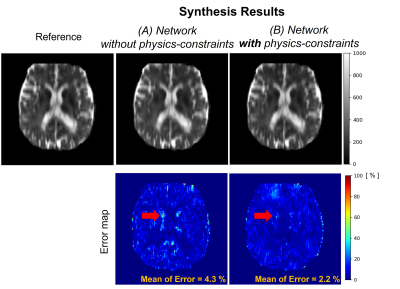
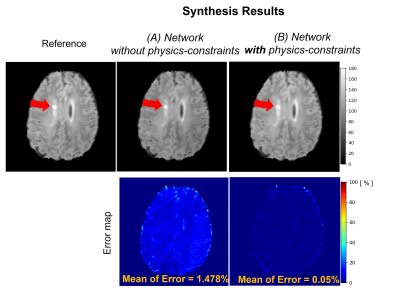
Figure 2 illustrates the prediction results of quantitative parameter maps from U-Nets ($$$U_{T1}$$$, $$$U_{T2}$$$, $$$U_{M0}$$$). Our predicted T1, T2, and M0 maps show ground-truth-like image with minimal error. Therefore, physics-constrained images from the predicted parameter maps are accurate. In Figure 3 and 4, we present the synthesis results of T2w and FLAIR contrasts, respectively. For both tissue contrasts, our physics-constrained network showed the improved synthesis quality in preserving fine details of ventricles and periventricular lesion in MS patients as highlighted in difference images. This indicates that physics-constraint posed by Bloch equations enhances the missing tissue contrast synthesis.
We also report quantitative evaluation scores for parameter map prediction and missing contrast synthesis in Table 1. Our proposed physics-constrained network accurately predicts parameter maps and produces significantly lower NRMSE and higher PSNR and SSIM than the original U-Nets that synthesize missing tissue contrasts directly from a T1-weighted image.

Conclusions & Disscusions

In this study, we proposed a synthesis neural network with physics-constraints. Comparing with a direct synthesis network without constraints, we achieved the significant improvement in SSIM , PSNR, and NRMSE values.
Our method needs only T1w to generate parameter maps, T2-weighted and FLAIR, potentially leading to time savings. The shorter protocol length may help when scanning patients who have difficulty lying still. The method may also be useful for retrospective analysis of imaging data. Future work will focus on the consistency of the results.

Acknowledgements

This research was supported by the MSIT (Ministry of Science, ICT), Korea, under the High-Potential Individuals Global Training Program (2021-0-01553) supervised by the IITP (Institute for Information & Communications Technology Planning & Evaluation).

References

1. Ye, D. H., Zikic, D., Glocker, B., Criminisi, A., & Konukoglu, E. (2013, September). Modality propagation: coherent synthesis of subject-specific scans with data-driven regularization. In International Conference on Medical Image Computing and Computer-Assisted Intervention (pp. 606-613). Springer, Berlin, Heidelberg.

2. Dewey, B. E., Zhao, C., Reinhold, J. C., Carass, A., Fitzgerald, K. C., Sotirchos, E. S., ... & Prince, J. L. (2019). DeepHarmony: A deep learning approach to contrast harmonization across scanner changes. Magnetic resonance imaging, 64, 160-170.

3.Ronneberger, O., Fischer, P., & Brox, T. (2015, October). U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention (pp. 234-241). Springer, Cham.

4. Johnson, J., Alahi, A., & Fei-Fei, L. (2016, October). Perceptual losses for real-time style transfer and super-resolution. In European conference on computer vision (pp. 694-711). Springer, Cham.

5. Kober, T., Granziera, C., Ribes, D., Browaeys, P., Schluep, M., Meuli, R., ... & Krueger, G. (2012). MP2RAGE multiple sclerosis magnetic resonance imaging at 3 T. Investigative radiology, 47(6), 346-352.

6. Mugler III, J. P. (2014). Optimized three‐dimensional fast‐spin‐echo MRI. Journal of magnetic resonance imaging, 39(4), 745-767.