0775

In vivo myelin thickness estimates from DIffusion-Prepared Phase Imaging (DIPPI)
Michiel Cottaar1, Wenchuan Wu1, Karla Miller1, and Saad Jbabdi1
1Wellcome Centre for Integrative Neuroimaging, FMRIB, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom

Synopsis

DIPPI is a novel sequence that allows the measurement of the off-resonance field experienced by intra-axonal water, which in myelinated axons is modulated by the surrounding myealin sheath allowing for estimation of the g-ratio. Unlike other g-ratio imaging methods, DIPPI does not rely on combining multiple modalities and can provide g-ratio estimates for individual crossing fibre populations rather than averaged over voxels. We present the first in-vivo DIPPI measurements and correct it for confounds such as subject movement and eddy currents. We then estimate the g-ratio in multiple white matter tracts from the processed off-resonance field maps.

Introduction

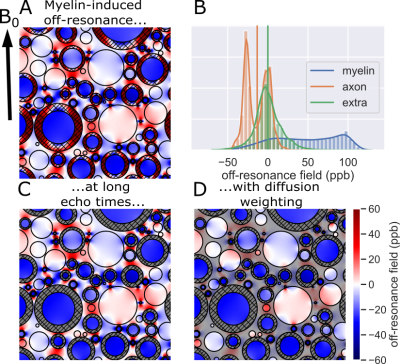
Within an external magnetic field, myelin’s magnetic susceptibility alters the local off-resonance magnetic field1 (Figure 1A,B). In particular, within the intra-axonal water there is a simple relationship between the myelin-induced off-resonance field and the thickness of the surrounding myelin sheath1:
$$\omega_{\text{myelin}\rightarrow\text{intra}}=\chi_\text{A}\omega_\text{Larmor}\log g\sin^2\theta$$
where $$$\chi_\text{A}\approx-100\text{ppb}$$$1 and $$$\omega_\text{Larmor}$$$ are constants (anisotropic magnetic susceptibility of myelin and Larmor frequency, respectively), $$$g$$$ is the g-ratio defined as the ratio of the inner over outer radius of the myelin sheath, and $$$\theta$$$ is the angle between the fibre orientation and the main magnetic field.

After sufficiently strong diffusion weighting, the remaining signal is dominated by the intra-axonal water (Figure 1C,D)2-4. The off-resonance field of the intra-axonal water still visible after diffusion weighting (Figure 1D) can be used to estimate the myelin thickness using equation 15.

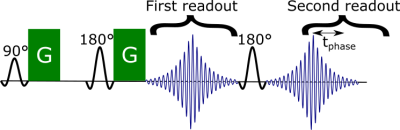
To address movement-induced phase offsets during the diffusion weighting, we proposed a novel sequence5 which adds a second readout with an asymmetric echo after a standard Stejskal-Tanner sequence6 (Figure 2). The phase offset between the two readouts can be used to estimate the intra-axonal off-resonance frequency and hence the myelin thickness.

Methods

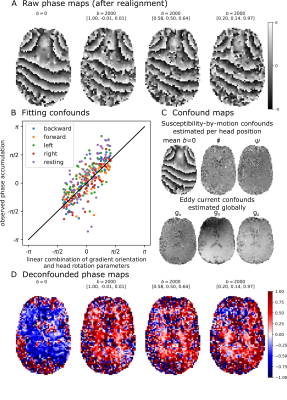
We acquired for the first in-vivo DIPPI data in a single subject on a Magnetom 7T scanner. To investigate the $$$\sin^2\theta$$$ dependence (eq. 1) data was acquired at five different head positions: left (14°), right (11°), forward (19°), backward (16°), and rest (angles relative to rest). For each head position data we acquired: 60 gradient orientations with $$$b=2\text{ms}/\mu\text{m}^2$$$ interspersed with 4 $$$b=0$$$ scans and a single $$$b=0$$$ scan with opposite phase encoding for distortion correction. Scan parameters were phase accumulation time between readouts ($$$t_\text{phase}$$$) of 20 ms, 20 slices, 3 mm3 isotropic resolution, TE1/TE2/TR=78/116/4000 ms, GRAPPA=2, scan time of 4:28 minutes per head position.

Images were aligned and distortion-corrected using FSL’s topup7 and eddy8. Afterwards the different head orientations were registered into a common space. The result is a set of aligned maps showing the phase accumulation (Figure 3A).

The phase maps were deconfounded by removing:
  1. Mean $$$b=0$$$ phase map estimated separately for each head position to correct for changes in the B0 field.
  2. Linear trends with the gradient orientation ($$$g_{x/y/z}$$$) to correct for eddy current’s contribution to the off-resonance field.
  3. Linear trend with the head rotation parameters from eddy to correct for variations in the B0 field due to involuntary movement within each head position.
First, we estimated in each voxel the best-fit linear trends (Figure 3B) leading to the maps shown in Figure 3C. These maps were then used to deconfound each phase map based on its head position, gradient orientation and eddy rotation parameters. In the resulting deconfounded phase maps (Figure 3D) the variations of phase with gradient orientations should be dominated by the myelin-induced off-resonance field5.

To test this dominance of the myelin-induced off-resonance field, we estimate fibre orientations by running a ball-and-stick model9 on the magnitude data from the first readout. In each voxel with crossing fibres we then estimated the phase accumulation associated with each crossing fibre. This phase accumulation was modelled as the sum of a contribution from the large-scale B0 field (which we assume is the same for both crossing fibres) and a fibre-specific myelin-induced contribution (eq. 1). Using multiple head positions improves the feasibility of estimating the g-ratios by measuring the phase accumulation for different $$$\sin^2\theta$$$ (eq. 1)5.

To associate the g-ratios with white matter tracts, tractography based on protocols from FSL's XTRACT10 was run on higher-resolution (1.4x1.4x1.2 mm) diffusion-weighted data (64 directions, $$$b=1\text{ms}/\mu\text{m}^2$$$).

Results

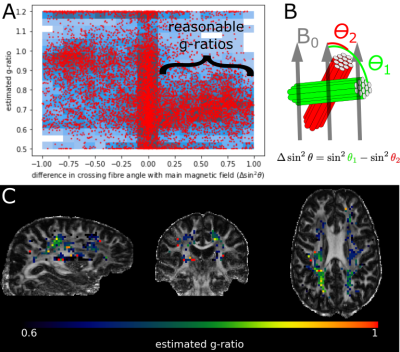
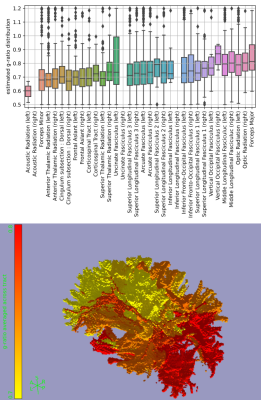
Fibres perpendicular to the main magnetic field experience the strongest myelin-induced off-resonance (i.e., large $$$\sin^2\theta$$$ in eq. 1). We expect a robust g-ratio estimate when such perpendicular fibres cross other fibres parallel to the main magnetic field (i.e., large $$$\Delta\sin^2\theta$$$ as defined in Figure 4B), because the B0 field estimated from signals associated with parallel fibres contains minimal myelin confounding. This is found in Figure 4A, where reasonable g-ratios (around 0.7) are estimated for fibres with $$$\Delta \sin^2\theta>0.1$$$.

The estimated g-ratios for those fibres are shown in Figure 4C. Note that these are not voxel-averaged g-ratio estimates, but are in fact associated with a single crossing fibre population in that voxel (i.e., the fibre population at a larger angle with respect to the main magnetic field). When averaged across tracts, some trends emerge with the optic radiation and the forceps major being much less myelinated (i.e., high g-ratio) than the acoustic radiation and the forceps minor (Figure 5). However, it should be noted that the estimates of the acoustic radiation and the forceps major are based on very few voxels, because in its present form DIPPI only provides g-ratio estimates from horizontal fibres in crossing fibre regions of which these tracts have only a small number within our field of view.

Future work

  1. Further reduce the noise during the acquisition, reconstruction, and preprocessing.
  2. Use microstructural models to describe the phase accumulation as a function of b-value. This should allow for g-ratio estimates in single-fibre regions and for fibres more parallel to the main magnetic field (in particular if combined with noise reduction).
  3. Validate the g-ratios estimated from DIPPI using other myelin mapping techniques and post-mortem electron microscopy.

Acknowledgements

Wenchuan Wu and Michiel Cottaar contributed equally to this work.

Michiel Cottaar and Saad Jbabdi are funded by a Wellcome Collaborative Award (grant no. 215573/Z/19/Z) and a Wellcome Senior Research Fellowship (grant no.221933/Z/20/Z). Karla Miller is funded by the Wellcome Trust (grant no. 202788/Z/16/Z). Wenchuan Wu is funded by the Royal Academy of Engineering (grant no. RF201819/18/92). The Wellcome Centre for Integrative Neuroimaging (WIN) is supported by core funding from the Wellcome Trust (grant no. 203139/Z/16/Z).

References

1 Wharton, Samuel, and Richard Bowtell. ‘Effects of White Matter Microstructure on Phase and Susceptibility Maps.’ Magnetic Resonance in Medicine 73, no. 3 (2015): 1258–69. https://doi.org/10.1002/mrm.25189.

2 McKinnon, Emilie T, Jens H Jensen, G Russell Glenn, and Joseph A Helpern. ‘Dependence on B-Value of the Direction-Averaged Diffusion-Weighted Imaging Signal in Brain.’ Magnetic Resonance Imaging 36 (2017): 121–27. https://doi.org/10.1016/j.mri.2016.10.026.

3 Veraart, Jelle, Els Fieremans, and Dmitry S Novikov. ‘On the Scaling Behavior of Water Diffusion in Human Brain White Matter.’ Neuroimage 185 (2019): 379–87. https://doi.org/10.1016/j.neuroimage.2018.09.075.

4 Lundell, Henrik, Chloé Najac, Marjolein Bulk, Hermien E. Kan, Andrew G. Webb, and Itamar Ronen. ‘Compartmental Diffusion and Microstructural Properties of Human Brain Gray and White Matter Studied with Double Diffusion Encoding Magnetic Resonance Spectroscopy of Metabolites and Water’. NeuroImage nil, no. nil (2021): 117981. https://doi.org/10.1016/j.neuroimage.2021.117981.

5 Cottaar, Michiel, Wenchuan Wu, Benjamin C. Tendler, Zoltan Nagy, Karla Miller, and Saad Jbabdi. ‘Quantifying Myelin in Crossing Fibers Using Diffusion‐prepared Phase Imaging: Theory and Simulations’. Magnetic Resonance in Medicine nil, no. nil (2021): mrm.28907. https://doi.org/10.1002/mrm.28907.

6 Stejskal, E.O., and Tanner J.E. ‘Spin Diffusion Measurements: Spin Echoes in the Presence of a Time Dependent Field Gradient’. The Journal of Chemical Physics, 1965. https://doi.org/10.1063/1.1695690.

7 Andersson, Jesper L R, Stefan Skare, and John Ashburner. ‘How to Correct Susceptibility Distortions in Spin-Echo Echo-Planar Images: Application to Diffusion Tensor Imaging.’ Neuroimage 20, no. 2 (2003): 870–88. https://doi.org/10.1016/S1053-8119(03)00336-7.

8 Andersson, Jesper L R, and Stamatios N Sotiropoulos. ‘An Integrated Approach to Correction for Off-Resonance Effects and Subject Movement in Diffusion MR Imaging.’ Neuroimage 125 (2016): 1063–78. https://doi.org/10.1016/j.neuroimage.2015.10.019.

9 Behrens, T E J, H Johansen Berg, S Jbabdi, M F S Rushworth, and M W Woolrich. ‘Probabilistic Diffusion Tractography with Multiple Fibre Orientations: What Can We Gain?’ Neuroimage 34, no. 1 (2007): 144–55. https://doi.org/10.1016/j.neuroimage.2006.09.018.

10 Warrington, S, K L Bryant, A A Khrapitchev, J Sallet, M Charquero-Ballester, G Douaud, S Jbabdi, R B Mars, and S N Sotiropoulos. ‘XTRACT - Standardised Protocols for Automated Tractography in the Human and Macaque Brain.’ Neuroimage (2020): 116923. https://doi.org/10.1016/j.neuroimage.2020.116923.


Figures

DIPPI concept; A) Map of the myelin-induced off-resonance field for a set of myelinated and unmyelinated cylindrical axons. B) Distribution of the field in panel A. After diffusion-weighting the remaining signal should be dominated by the intra-axonal water, because the myelin water signal has decayed at long echo times due to its short T2 (C) and the extra-axonal water contribution is substantially reduced due to its higher diffusivity (D).

proposed DIffusion-Prepared Phase Imaging (DIPPI) sequence; A second readout with an asymmetric spin echo is added after a Stejskal-Tanner diffusion MRI sequence6. The phase offset between the two readouts is measured. This phase offset is proportional to the phase accumulation time $$$t_\text{phase}$$$ and the off-resonance field experienced by the water signal still visible after the diffusion weighting on the left. This water signal originates predominantly from the intra-axonal space (Figure 1D)2-4.

deconfounding; A) phase accumulation maps after alignment and distortion correction. B) In every voxel we estimate the phase contributions from eddy currents and involuntary head rotations ($$$\phi$$$ and $$$\psi$$$) using a linear fit. C) Resulting maps of susceptibility-by-motion (top) and eddy current (bottom) confounds. No smoothing was applied. D) Resulting phase accumulation maps after subtracting out the confound phase contributions illustrated in panel C (note the reduced range of the color bar compared to panel A).

g-ratio estimation; A) Each dot represents the g-ratio estimated for a crossing fibre population (blue background is a density map). The x-axis is defined in panel B as the difference in $$$\sin^2\theta$$$ between the fibre for which the g-ratio was estimated (green) and the crossing fibre (red). C) g-ratio map for those fibres more perpendicular to the B0 than their crossing counterpart ($$$\Delta\sin^2\theta>0.1$$$).

tract myelin thickness; Box-plot of g-ratio distribution across tracts identified using FSL’s XTRACT7. Because DIPPI estimates g-ratios on a per-fibre, not a per-voxel basis, we only consider the g-ratios along the fibre population aligned with the tract. The bottom shows a map of the tracts coloured by their average g-ratio.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)
0775
DOI: https://doi.org/10.58530/2022/0775