0768
Rapid Multi-shell Diffusion MRI Enabled by Learning Compact and Rotation Invariant q-Space Representations1University of Iowa, Iowa City, IA, United States, 2GE Healthcare, Waukesha, WI, United States
Synopsis
A modified reconstruction is proposed for highly accelerated dMRI. The method employs machine learning in a model-based setting. The current work improves the generalizability of the deep-learned plug-and-play prior employed in the reconstruction, for enabling utilization of the reconstruction from a wide range of acquisition settings. This is achieved by learning a compact q-space representation in a rotation invariant space. The method is tested for the reconstruction of combined multi-band and in-plane accelerated data from both single-shell and multi-shell experiments. The reconstruction error is shown to be less than 3% for net acceleration of R=12 for single- and multi-shell cases.
Introduction
Diffusion-weighted magnetic resonance imaging (dMRI) is a widely used neuroimaging technique that provides quantitative measures of brain microstructural and connectivity changes in-vivo. For accurate microstructure and connectivity studies, the competing demands of dense q-space coverage and k-space coverage need to be addressed. Accelerated data acquisition combining multi-band (MB) imaging and parallel imaging (i.e, in-plane undersampling) is typically utilized for such studies. However, the reconstruction of the above data is challenging due to the heavy aliasing.Prior studies have explored the utilization of machine learning to enable such reconstructions.1-3 The end-to-end reconstruction in [1] employs a UNET-based architecture to provide intermediate image and phase information, which is utilized in a model-based reconstruction. The qModeL2-3 approach combines a pre-learned q-space prior in a plug-and-play fashion with a model-based reconstruction. Compared to the end-to-end approach, the training demands of the plug-and-play approach are relatively low. Recently, utilization of the qModeL approach for the reconstruction of q-space data for a wide range of acquisition settings was demonstrated both for single-shell and multi-shell dMRI studies2-3.
The training involved in the qModeL approach pertains to the pre-learning of a compact q-space representation. Particularly, the specific q-space (i.e., b-shells and gradient directions) to which the data belongs, is pre-learned from training data using a denoising autoencoder (DAE). A disadvantage with this approach is that the DAE cannot handle the reconstruction of arbitrary datasets that do not match the q-space of the training data. In such scenarios, re-training is needed. In this work, we reformulate the pre-learning involved in qModeL to a rotation-invariant q-space representation. This approach enables the plug-and-play prior to being utilized in a wider q-space acquisition setting, thus further improving the flexibility of the qModeL framework.
Methods
The qModeL cost function, which jointly reconstructs all the diffusion weighted images (DWIs) from a MB-accelerated acquisition is given by:$$ \mathbf {S^{^*}_{\scriptscriptstyle b}}\!\! = arg \min_{\tilde{ \mathbf S_{\scriptscriptstyle b}}} ||{\mathcal {A}_{b}({\mathbf S_{\scriptscriptstyle b}})-\widehat{\mathbf Y }}||_2^2 + \lambda_1 ~ ||{\mathcal P_{\Theta}(\mathbf S_{\scriptscriptstyle b}) }||_2^2 + \lambda_2 ~||{ \mathbf S_{\scriptscriptstyle b}}||_{TV}\\ \text{where } \mathcal P_{\Theta}\big({\mathbf S}_{b}\big) ={\mathcal D_{\Theta}\big({\mathbf S}_{b}\big) -{\mathbf S}_{b}}.$$
Here, the model-based reconstruction explicitly enforces data consistency to the measured data $$$\widehat{\mathbf Y }$$$ using the first term (details in figure 1). The reconstruction is further augmented using a q-space prior (second term) and a total-variation (TV) prior (third term). The second term helps to incorporate the deep-learned q-space prior into the reconstruction. Here, $$$\mathcal D_{\Theta}$$$ denotes the compact q-space representation, which is the encoder-decoder mapping pre-learned by the DAE. At every iteration, $$$\mathcal D_{\Theta}$$$ is utilized to compute the projection error of the reconstructed q-space signal onto the pre-learned q-space, $$$\mathcal P_{\Theta}$$$, which is minimized during the optimization. Note that by virtue of the pre-training, the number of inputs of the DAE is fixed to the number of q-space points in the training data. Hence, a test dataset involving a set of q-space points that differ from that of the training data leads to invalid reconstruction. To derive a more flexible plug-and-play prior, we re-formulate $$$\mathcal P_{\Theta}$$$ as follows:
$$ \mathcal P_{\Theta}\big({\mathbf S}_{b}\big) ={\cal{H}}_{q_r}^{\dagger}\big\{{\mathcal D_{\Theta}^{q_t}\big(\underbrace{{\cal{H}}_{q_r}\{~{\mathbf S}_{b}\}}_{\mathbf C_{l,m}}~\big) \big\}-{\mathbf S}_{b}}.$$
Here, $$${\cal{H}}_{q_r}\{~{\mathbf S}_{b}\}$$$ stands for the spherical harmonics (SH) transformation that transforms the raw q-space signal to the SH basis to derive the SH coefficients $$${\mathbf C_{l,m}}$$$, for a given order $$$l$$$ and degree $$$m$$$. $$${\cal{H}}_{q_r}^{\dagger}$$$ denotes the inverse transformation. Therefore, unlike the previous DAE which was trained on the raw q-space signals, the new DAE, $$${\mathcal D_{\Theta}^{q_t} }({\mathbf C_{l,m}})$$$, is trained on the SH coefficients of the training signals. The advantage is that arbitrary test data with a different set of q-space points can utilize the SH transform to make use of the plug-and-play prior and hence can be reconstructed using the pre-learned framework.
To evaluate the new formulation termed qModeL-SH, test datasets were collected from in-vivo acquisition, the details of which are provided in Table 1. The k-space sampling was performed using a 4-shot EPI sequence, which was retrospectively under-sampled for studying the in-plane accelerated cases. For every q-space sample, only 1 random k-space shot was retained, giving a total acceleration of 12 (MB=3,Rin-plane=4).
Results
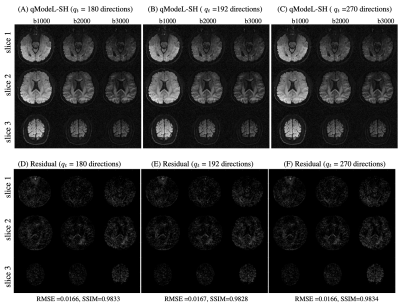
Figure 2 shows the equivalence of the qModeL and qModeL-SH formulation shown for the case with no under-sampling. Figure 3 demonstrates the flexibility of the qModeL-SH formulation, where the training q-space sampling points do not match the test q-space sampling points (tested with no under-sampling). Figure 4 shows the reconstruction of the MB- and in-plane accelerated case corresponding to a net acceleration of R=12 using the qModeL-SH formulation. Finally, Figure 5 shows the reconstruction of the multi-shell data for the net acceleration of R=12. The root-mean-squared error (RMSE) calculated with respect to the reconstruction with no under-sampling, were 0.018 and 0.016 respectively for single- and multi-shell cases. The structure similarity index (SSIM) were 0.99 and 0.98 respectively for single- and multi-shell cases.Discussion
A new reconstruction method was presented for the recovery of MB- and in-plane accelerated dMRI data. The method makes use of model-based deep learning in a rotation invariant setting facilitating the recovery of q-space data from a wide range of acquisition settings.Acknowledgements
Financial support for this study was provided by grants 1R01EB031169, R01AG067078, 1R01EB022019- 01A, and 1 I01 RX002987. This work was conducted on MRI instruments funded by 1S10OD025025-01 and 1S10RR028821-01. This project was supported in part by a 2020 NARSAD Young Investigator Grant from the Brain & Behavior Research Foundation.References
[1] Bilgic, B., Chatnuntawech, I., Manhard, M. K., Tian, Q., Liao, C., Iyer, S. S., Cauley, S. F., Huang, S. Y., Polimeni, J. R., Wald, L. L., & Setsompop, K. (2019). Highly accelerated multishot echo planar imaging through synergistic machine learning and joint reconstruction. Magnetic Resonance in Medicine, 82(4), 1343–1358. https://doi.org/10.1002/mrm.27813
[2] Mani, M., Magnotta, V. A., & Jacob, M. (2021). qModeL: A plug‐and‐play model‐based reconstruction for highly accelerated multi‐shot diffusion MRI using learned priors. Magnetic Resonance in Medicine, 86(2), 835–851. https://doi.org/10.1002/mrm.28756
[3] Mani, M., Magnotta, V. A., & Jacob, M. (2021). Highly Accelerated Multi-shot EPI based Diusion MRI Using SMS and Joint k-q Under-sampling Enabled Using Deep Learned Manifold Priors, ISMRM 2021.
Figures

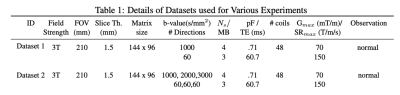
Figure 2: Compariosn of qModeL and qModeL SH reconstruction. Two representative DWIs reconstructed from dataset 1 : (A) using qModeL, with DAE trained on raw diffusion signal, (B) using qModeL-SH with DAE trained on the SH coefficients, and (C) their difference. Here, the training was done using the same set of q-space points for both cases. The difference image shows that the qModeL and qModeL-SH reconstruction provide equivalent results. The experiment is for the case with MB=3 and no in-plane acceleration.
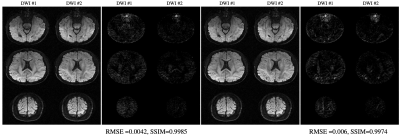
Figure 3: qModeL-SH reconstruction of the test data for the case where the training data belongs to a different set of q-space sampling points : (A) show reconstruction where the SH coefficient training was performed using 64 q-space points, and (B) show the residual with respect to qModeL reconstruction (amplified 20X). (C) show reconstruction where the SH coefficient training was performed using 90 q-space points, and (D) show the residual with respect to qModeL reconstruction (amplified 20X). All images are displayed on the scale [0 1].