Introduction

Microstructural changes in the intra-axonal space (IAS) of brain white matter (WM) can occur due to healthy structural plasticity or disease. Sensitivity to such changes with diffusion magnetic resonance imaging (MRI) is key to understanding how diseases progress in the WM. Monte Carlo (MC) simulations of diffusion within realistic axonal phantoms, based on histological quantifications of axonal morphology, aid the design of diffusion MRI protocols that target IAS changes. Current frameworks^1,2 aim to produce realistic phantoms by inputting a set of target parameters (e.g. axon diameter distribution and density) and packing axons. However, if the target density is high – as expected in WM – the packing algorithm may not succeed in maintaining the target parameters. This is problematic when trying to model the IAS with specific parameters.

We present MISA, a simple framework to generate Microstructure Informed Synthetic Axons from descriptors of axon morphology. We show that this enables the generation of synthetic axons that match the properties of axons segmented from 3D histology in terms of morphology, and transverse and parallel apparent diffusion coefficients (ADC).

Methods

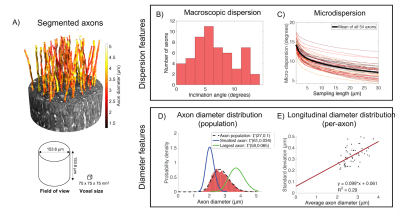
Morphological descriptors of axons
MISA axons were modelled on 54 segmented axons from a 3D x-ray nano-holotomography (XNH) volume of the vervet monkey splenium; the data and morphological analysis are described in Andersson et al.³ and are shown in Figure 1. In short, axonal “macrodispersion” was defined as the inclination angle between the average direction of the 54-axon bundle and the main direction of each individual axon. “Microdispersion” was defined as the mean inclination angle between the axon’s main direction and its trajectory divided into segments of length $$$L$$$. Diameters were evaluated at 150 nm intervals along the axonal trajectories. The pooled distribution of all diameters in the 54-axon population is shown in Figure 1D, and the relationship between mean and standard deviation of axon diameter variations along single axons is shown in panel E.

MISA algorithm
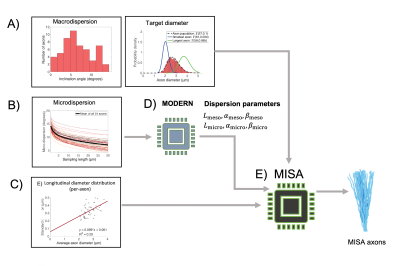
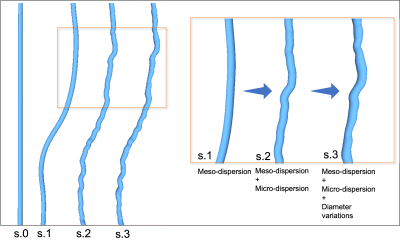
MISA (Figure 2) is a multistage algorithm that builds realistic axons by step-wise increasing the morphological complexity towards desired microstructural properties, as shown in Figure 3. In step 0, a cylinder with target diameter $$$d$$$ is given a random orientation from a macroscopic orientation distribution (e.g. a distribution fitted to Figure 1B). The target $$$d$$$ can be drawn from a distribution e.g. that in Figure 1D. In step 1, the cylinder midline is discretized into segments of length $$$L_{\text{meso}}$$$. Each segment is given an inclination angle sampled from a gamma distribution, $$$\Gamma_{\text{meso}}(\alpha_{\text{meso}},\beta_{\text{meso}})$$$. In step 2, the trajectory is further discretized into segments of length $$$L_{\text{micro}}$$$ where $$$L_{\text{micro}}< L_{\text{meso}}$$$. Again, the segments are assigned orientations that are picked from a second distribution, $$$\Gamma_{\text{micro}}(\alpha_{\text{micro}},\beta_{\text{micro}})$$$. We used the Multi-Objective Differential Evolution for Realistic Numerical Axons (MODERN) framework⁴ to learn the optimal discretization lengths ($$$L_{\text{micro}}$$$ and $$$L_{\text{meso}})$$$ and dispersion parameters ($$$\alpha_{\text{meso}}$$$, $$$\beta_{\text{meso}}$$$, $$$\alpha_{\text{micro}}$$$, $$$\beta_{\text{micro}}$$$) needed to replicate the mean microdispersion curve in Figure 1C, with 15 µm < $$$L_{\text{meso}}$$$ < 30 µm and 0.5 µm < $$$L_{\text{micro}}$$$ < 2 µm. Finally, in step 3, MISA applies diameter variations at intervals of $$$L_{\text{micro}}$$$, given a standard deviation of the diameter distribution along single axons – in this case provided by Figure 1E.

Monte-Carlo simulations
We generated 54 MISA axons using the inputs in Figure 1. Each was assigned the same target mean diameter as a corresponding XNH axon to focus only on the variability due to the randomly generated microdispersion and diameter variations. MC simulations⁵ of diffusion were performed for up to 50 ms in the XNH and MISA axons. Spins were uniformly initialised within each axon at a density of 1 µm$$$^{-3}$$$ and a minimum distance of 20 µm from the ends to prevent their escape. An ex vivo diffusivity of $$$D_0 = 0.6 \cdot 10^{-9} \text{m}^2\text{/s}$$$ was used as in Andersson et al.³. The ADCs parallel and transverse to the bundle main direction were computed using $$$ \left \langle (\Delta r)^2 \right \rangle = 2Dt $$$ where $$$(\Delta r)$$$ represents the mean-squared displacement in a given direction, $$$D$$$ is the ADC and $$$t$$$ is the diffusion time.

Results and Discussion

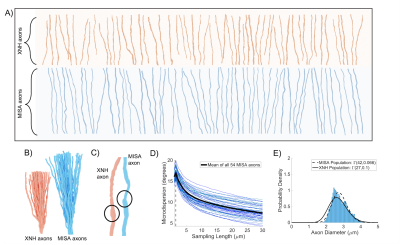
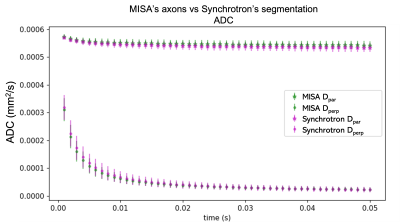
The MISA axons resemble those from XNH (Figures 4A-C) and capture their morphological variations. The mean trend in microdispersion across all MISA axons (black line, Figure 4D) is very similar to that in Figure 1C, including the spread around the mean. Small discrepancies between the pooled axon diameter distributions (<300 nm shift of the mean) in Figure 4E are expected due to limited sample size and the simple linear fit used to define the standard deviation of diameter variations in the generated axons (Figure 1E). Finally, Figure 5 shows how we obtain time-dependent ADCs similar to those of the XNH axons by mimicking the previously presented characteristics.

Conclusion

The MISA framework allows for fast generation of realistic axons given statistical input parameters of morphology from 3D electron microscopy^6–8 or XNH³. MISA can be used to generate anatomical region- or species-specific IAS substrates, as well as validate more complex frameworks that incorporate axonal packing. It outputs 3D meshes for MC simulations which are key to understanding the diffusion MRI signals from a given protocol. MISA will be freely available as a Blender add-on.

Acknowledgements

M.A. and H.M.K. were supported by Capital Region Research Foundation Grant A5657 (principal investigator: T.B.D.) We acknowledge access to the facilities and expertise of the CIBM Center for Biomedical Imaging, a Swiss research center of excellence founded and supported by Lausanne University Hospital (CHUV), University of Lausanne (UNIL), Ecole Polytechnique Fédérale de Lausanne (EPFL), University of Geneva (UNIGE), and Geneva University Hospitals (HUG). This work was supported by EPFL through the use of the facilities of its Scientific IT and Application Support Center (SCITAS). This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 754462 (MP).