0749
Rigorous Uncertainty Estimation for MRI Reconstruction1Electrical Engineering and Computer Sciences, University of California, Berkeley, Berkeley, CA, United States, 2International Computer Science Institute, University of California, Berkeley, Berkeley, CA, United States
Synopsis
Deep-learning (DL)-based MRI reconstructions have shown great potential to reduce scan time while maintaining diagnostic image quality. However, their adoption has been plagued with fears that the models will hallucinate or eliminate important anatomical features. To address this issue, we develop a framework to identify when and where a reconstruction model is producing potentially misleading results. Specifically, our framework produces confidence intervals at each pixel of a reconstruction image such that 95% of these intervals contain the true pixel value with high probability. In-vivo 2D knee and brain reconstruction results demonstrate the effectiveness of our proposed uncertainty estimation framework.
Introduction
Deep learning (DL)-based reconstruction methods have shown great potential for efficient image reconstruction from undersampled k-space measurements1-5. However, a substantial risk in DL-based reconstruction is hallucination or elimination of important anatomical features from the image6. To address this concern, we seek uncertainty estimates which tell us when we can trust a reconstruction. While existing7-11 methods have shown promising results in estimating uncertainty maps, they do not come with statistical guarantees. Furthermore, they often require computational overhead (such as running multiple reconstructions) and/or modifications to the reconstruction network (e.g. nonstandard training procedures) that may sabotage its accuracy. In this work, we propose a simple and rigorous uncertainty estimation framework that works without modifying or retraining the reconstruction network (Figure 1). Our technique provides a rigorous finite-sample statistical guarantee. Our key contribution is the development of a new form of Risk-Controlling Prediction Set (RCPS)12 tailored to MRI reconstruction that outputs image-valued confidence intervals containing at least $$$(1-\gamma)$$$ (e.g., 95%) of the ground truth pixel values. Our in-vivo knee and brain results probe the quality of our uncertainty estimation model, which allows us to identify specific regions where the model performs poorly.Methods
Our method trains an uncertainty estimation network, then calibrates that network to achieve a rigorous guarantee. We will now detail these two subroutines.1. Training the uncertainty estimation network
Given a pre-trained reconstruction network, e.g., MoDL4, the uncertainty estimation network predicts the absolute residual error for that network (Figure 2a). The pre-trained network $$$G_w$$$ takes the zero-filled reconstruction and maps it to $$$\hat{\mathrm{x}}_i$$$, an estimate of the ground truth image $$$\mathrm{x}_i$$$. Our uncertainty estimation network $$$f_\theta$$$ is trained to output an estimate $$$\hat{\mathrm{err}}_i$$$ of the magnitude of the residual error $$$|\mathrm{x}_i-\hat{\mathrm{x}}_i|$$$. In practice, the input to $$$f_{\theta}$$$ is actually several concatenated features from each iteration of $$$G_w$$$. After training is complete, we can now map new, unseen under-sampled inputs to the reconstructed images and uncertainty estimates in one forward pass. However, note that we have no guarantee that $$$\hat{\mathrm{err}}_i$$$ does well at estimating the pixel-wise error, so we will need to calibrate it.
2. Calibration of the heuristic uncertainty estimates
Once the uncertainty estimation network is trained, we aim to calibrate its output using Risk-controlling Prediction Sets12 (Figure 2b) to achieve a statistical guarantee. We first select a subset of the validation set to form the calibration set $$$(\mathrm{x}_i,\hat{\mathrm{x}}_i,\hat{\mathrm{err}}_i),i=1,2,3,4,...N$$$ (typically $$$N \gtrapprox 1000$$$). Then, we calibrate a global scalar $$$\hat{\alpha}$$$ from the calibration set to ensure that, on average, at least ($$$1-\gamma$$$ ) of all pixels from the reference are within its confidence intervals $$$I^{(m,n)}_i = [\hat{\mathrm{x}}_i^{(m,n)}-\hat{\alpha}\cdot\hat{\mathrm{err}}_i^{(m,n)}, \hat{\mathrm{x}}_i^{(m,n)}+\hat{\alpha}\cdot\hat{\mathrm{err}}_i^{(m,n)}]$$$, for all pixel locations $$$(m,n)$$$ in an image of size $$$M \times N$$$. For example, choosing $$$\gamma=0.05$$$ and $$$\delta=0.1$$$ will result in 95% of the pixels being contained in their intervals with 90% probability. The detailed calibration procedure is described as follows. For a given image $$$\mathrm{x}_i$$$, we first define the loss $$L(\alpha)_i=\frac{|(m,n) : \mathrm{x}_i^{(m,n)} \notin I^{(m,n)}_i|}{MN}$$ as the fraction of pixels not included in their respective intervals. We compute the empirical risk over the calibration dataset and use the Upper Confidence Bound (UCB)15,16 procedure from12 with the WSR bound from15 to choose the smallest $$$\alpha$$$ that gives a RCPS,$$\mathbb{P}[\hat{R}^+(\alpha)\geq{R}(\alpha)]\geq (1-\delta),$$ where $$$\delta$$$ here is the desired violation rate (e.g., $$$\delta$$$=0.1). In short, the method involves computing the UCB $$$\hat{R}^+(\alpha)$$$ using a pointwise concentration inequality, then picking $$$\hat{\alpha}=\min\Big\{ \alpha : \hat{R}^+(\alpha’) < \gamma, \forall \alpha’ > \alpha \Big \}$$$. Deploying this choice of $$$\hat{\alpha}$$$ guarantees risk-control; we defer the proof of this fact to12.
Datasets and experimental setups
We evaluated the proposed framework on both 2D knee and brain fastMRI13 datasets. First, MoDL was trained for both anatomies using 5120 different slices. Then, we trained the uncertainty estimation network using the same training set, with a range of acceleration factors. Finally, we calibrated the heuristic uncertainty estimates using a calibration set of 1000 slices, while the validation set contained 2000 slices. We compared the heuristic uncertainty estimation results with the absolute residual errors. To evaluate the calibration procedure, we randomly split the validation set 2000 times. Each time, we calibrated a $$$\hat{\alpha}_j, j=1,2,3,...,2000$$$ and evaluated the empirical risk $$$\hat{R}_j$$$ on the rest of the validation set (evaluation set). We presented the histogram of the empirical risks to evaluate the empirical violation rate $$$\hat{\delta}$$$.Results
Figure 3 shows the uncertainty estimation results for the knee and brain datasets. The results show strong agreement between the uncertainty estimates and the blurred residual error.Figure 4 visualizes the textures and the corresponding uncertainty estimates. Zoomed-in details indicate that higher uncertainty appears in the regions where the reconstructed images did not successfully recover the fine textures and details.
Figure 5 shows the empirical risk distribution given different splits of calibration/evaluation sets. Histograms show that the empirical violation rate $$$\hat{\delta}$$$ hits nearly exactly $$$\delta$$$ for both $$$\gamma$$$, which demonstrates the tightness and validity of our calibration procedure.
Conclusions
This work presented a rigorous uncertainty estimation framework, which can provide precise uncertainty estimates backed by a finite-sample guarantee. Without any constraints on the reconstruction model, our framework acts as a plug-and-play module, and may significantly improve the accuracy of the diagnosis and clinical interpretation of DL-based reconstructions.Acknowledgements
The authors thank Dr. Uri Wollner from GE Healthcare for generating the sampling masks.References
1. Diamond, S., Sitzmann, V., Heide, F., & Wetzstein, G. (2017). Unrolled optimization with deep priors. arXiv preprint arXiv:1705.08041.
2. Schlemper, J., Caballero, J., Hajnal, J. V., Price, A., & Rueckert, D. (2017, June). A deep cascade of convolutional neural networks for MR image reconstruction. In International Conference on Information Processing in Medical Imaging (pp. 647-658). Springer, Cham.
3. Hammernik, K., Klatzer, T., Kobler, E., Recht, M. P., Sodickson, D. K., Pock, T., & Knoll, F. (2018). Learning a variational network for reconstruction of accelerated MRI data. Magnetic resonance in medicine, 79(6), 3055-3071.
4. Aggarwal, H. K., Mani, M. P., & Jacob, M. (2018). Modl: Model-based deep learning architecture for inverse problems. IEEE transactions on medical imaging, 38(2), 394-405.
5. Tamir, J. I., Stella, X. Y., & Lustig, M. (2019). Unsupervised deep basis pursuit: Learning reconstruction without ground-truth data. In Proceedings of the 27th Annual Meeting of ISMRM.
6. Muckley, M. J., Riemenschneider, B., Radmanesh, A., Kim, S., Jeong, G., Ko, J., ... & Knoll, F. (2021). Results of the 2020 fastmri challenge for machine learning mr image reconstruction. IEEE transactions on medical imaging, 40(9), 2306-2317.
7. Edupuganti, V., Mardani, M., Vasanawala, S., & Pauly, J. (2020). Uncertainty quantification in deep mri reconstruction. IEEE Transactions on Medical Imaging, 40(1), 239-250.
8. Narnhofer, D., Effland, A., Kobler, E., Hammernik, K., Knoll, F., & Pock, T. (2021). Bayesian Uncertainty Estimation of Learned Variational MRI Reconstruction. arXiv preprint arXiv:2102.06665.
9. Jalal, A., Arvinte, M., Daras, G., Price, E., Dimakis, A. G., & Tamir, J. I. (2021). Robust Compressed Sensing MRI with Deep Generative Priors. arXiv preprint arXiv:2108.01368.
10. Pawar, K., Egan, G. F., Chen, Z., Bahri, D. (2021, May). Estimating Uncertainty in Deep Learning MRI Reconstruction using a Pixel Classification Image Reconstruction Framework. In Proc. Intl. Soc. Mag. Reson. Med (No. 0276).
11. Zhang, Z., Romero, A., Muckley, M. J., Vincent, P., Yang, L., & Drozdzal, M. (2019). Reducing uncertainty in undersampled mri reconstruction with active acquisition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 2049-2058).
12. Bates, S., Angelopoulos, A., Lei, L., Malik, J., & Jordan, M. I. (2021). Distribution-free, risk-controlling prediction sets. arXiv preprint arXiv:2101.02703.
13. Zbontar, J., Knoll, F., Sriram, A., Murrell, T., Huang, Z., Muckley, M. J., ... & Lui, Y. W. (2018). fastMRI: An open dataset and benchmarks for accelerated MRI. arXiv preprint arXiv:1811.08839.
14. Paszke, A., Gross, S., Chintala, S., Chanan, G., Yang, E., DeVito, Z., ... & Lerer, A. (2017). Automatic differentiation in pytorch.
15. Waudby-Smith, I., & Ramdas, A. (2020). Estimating means of bounded random variables by betting. arXiv preprint arXiv:2010.09686.
16. Hoeffding, W. (1994). Probability inequalities for sums of bounded random variables. In The collected works of Wassily Hoeffding (pp. 409-426). Springer, New York, NY.
Figures
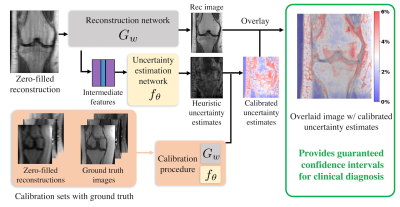
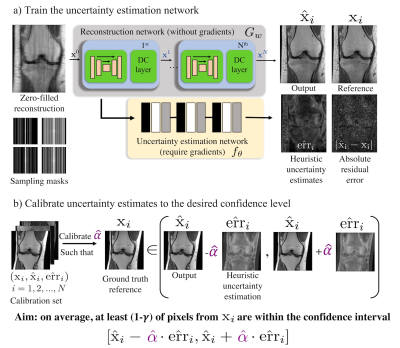
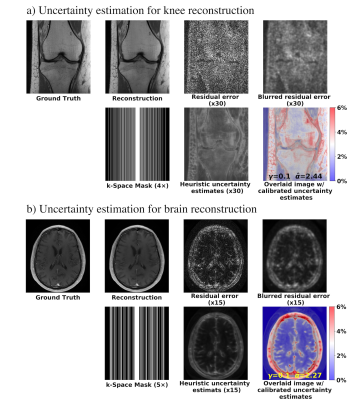
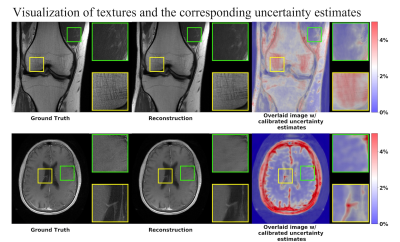
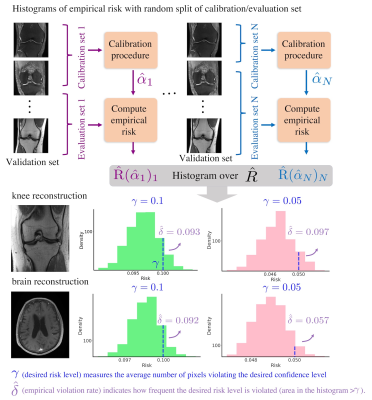
Figure 5. Empirical risk distribution under 2000 random split of calibration/evaluation sets for brain and knee datasets. Each split of the calibration set outputs an $$$\hat{\alpha}$$$ and the corresponding empirical risk $$$\hat{R}$$$, which roughly describes the number of pixels violating the desired risk/confidence level. Given a desired violation rate, the empirical violation rate $$$\hat{\delta}$$$ indicates how frequently the desired risk/confidence levels are violated. Comparisons of two desired risk/confidence levels $$$\gamma = 0.1, 0.05$$$ are presented.