0699
Unsupervised Diffeomorphic Registration for Even and Odd Echo Images with Applications to Point-of-Care MRI Reconstruction1Hyperfine, Guilford, CT, United States, 2New York University, New York City, NY, United States, 3Yale University, New Haven, CT, United States, 4Massachusetts General Hospital, Boston, MA, United States, 5Gaylord Specialty Healthcare, Wallingford, CT, United States
Synopsis
We present an unsupervised deep image registration framework for MR image reconstruction. Specifically, even and odd echo images from fast spin echo-based sequence are nonlinearly registered using a convolutional network that estimates the deformation field. The registered echo images are then averaged for noise reduction. The proposed framework was evaluated across four imaging contrasts (T1w, T2w, FLAIR, and DWI) from a low-field MR scanner and was found to outperform nonlinear registration from advanced normalization tools, yielding sharper image quality and preserving important pathology features.
Background
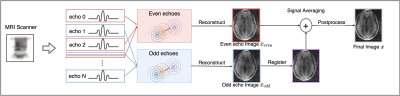
The primary advantage of portable point-of-care (POC) MRI is a low cost MRI design that provides mobility, stability, and clinically acceptable images in reasonable scan times1,2. At low-field3,4, SNR is inherently limited and several authors have investigated different techniques to improve image quality, such as interference removal5, deep learning-based reconstruction6 and denoising7. Alternative approach is to exploit fast spin echo (FSE) based sequences in which multiple echoes can be combined to increase the SNR. In the presence of system imperfections, however, the even and odd echoes must be treated and reconstructed separately, due to uncorrected eddy currents causing differential warping between the two. As such, deformable registration is necessary to align two images before they can be signal-averaged (Figure 1).Several works have been proposed for intra-contrast deformable registration,8-10 which is typically formulated as a minimization problem of the metric which quantifies the alignment after one image is deformed to the other. The limitation of classic methods is that hyperparameter tuning is required for different image content and contrast, and the convergence is often slow, making the tool difficult for generic use. More recently, deep learning-based deformable registration has been proposed,11-14 which enables large-scale training, broadening the robustness to a wider range of image content, as well as offering fast inference speed. In this work, we present unsupervised learning for a diffeomorphic registration framework that can be applied to register even and odd echo images, which generalizes across different contrast including T1-weighted, T2-weighted, fluid attenuated inversion recovery (FLAIR), and diffusion weighted images (DWI).
Materials and Methods
Imaging: A portable 64mT MRI scanner (Hyperfine SwoopTM) was deployed to 6 different acquisition sites and patients were recruited and provided consent under a protocol approved by an institutional review board. The patients underwent a different imaging imaging protocol, including T1w, T2w, FLAIR and DWI sequences. In total, 1861 imaging volumes were acquired, in which 60 were reserved for testing.Model and Training: Let $$$x_\text{even}$$$ and $$$x_\text{odd}$$$ denote 3D even and odd echo images. The goal is to find dense displacement field $$$\phi$$$ such that
$$ \text{argmin}_{\phi} \mathcal{L}(x_\text{even}, x_\text{odd}(\phi)) $$
In which the dense displacement field is estimated by a convolutional neural network $$$ \phi = f_{\theta}((x_\text{even}, x_\text{odd})$$$, shown in Figure 2. The network takes two echo images as the input and predicts the stationary velocity field $$$v$$$. The deformation field $$$\phi$$$ is given by integrating $$$v$$$ over $$$t = [0, 1]$$$, which is done by 5 iterations of scaling and squaring layers.15 We use 3D U-net architecture with 5 levels of downsampling.
The network is trained to minimize local normalized cross correlation (NCC) for $$$\mathcal{L}$$$:
$$\text{NCC}(x, y) = \frac{\sum_i \left((x_i- \mu_x) (y_i- \mu_y)\right)^2}{\sum_i (x_i- \mu_x)^2 \sum_i (y_i- \mu_y)^2}$$
Here $$$x$$$ and $$$y$$$ are local square windows in which the cross correlation is calculated and $$$\mu_x$$$ and $$$\mu_y$$$ are mean intensity within the windows. NCC over all local windows in the image is averaged to yield $$$\mathcal{L}$$$.
We trained one network for all contrasts. For data augmentation, we added random translation $$$\pm$$$ 3 pixels, anisotropic scaling in range (0.9, 1.2), flipping, and Gaussian noise up to $$$\sigma = 0.03$$$. We used Adam optimizer with a learning rate 10-4 and batch size 1. We trained the network for up to 300 epochs, which took approximately 1 week. All models were implemented in Tensorflow 2.3.2.
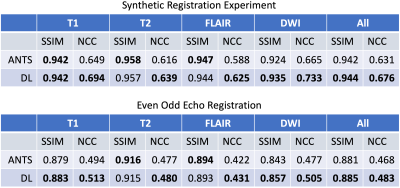
Evaluation: In the first experiment, random displacement fields were generated, simulating the range of distortion observed between even and odd echo images. The registration accuracy between two instances of deformed image were computed. In the second experiment, even and odd echo images were registered to one another. For both experiments, we used structural similarity index (SSIM) and NCC as the metrics. The proposed algorithm was compared to the SyN nonrigid registration algorithm from advanced normalization tools (ANTS)10. Finally, we applied the proposed algorithm to the reconstruction of MR images from a low-field portable MR system and the final reconstructed images were qualitatively evaluated.
Results
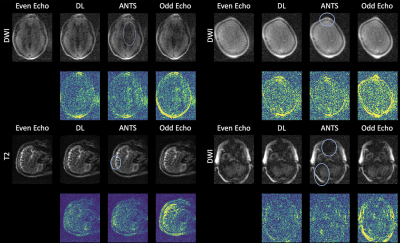
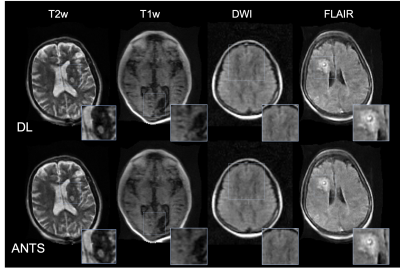
The results from the quantitative experiments are summarized in Figure 3. One can observe that overall DL outperformed the baseline method. The improvement in NCC was notable for T1-weighted, FLAIR and DWI images. An example of the results from even and odd echo image registration is shown in Figure 4. The overall performances of the two approaches were comparable. However, ANTS occasionally failed to completely register small local features. Figure 5 shows the outputs of the reconstruction pipeline incorporating nonlinear registration algorithms. We observe that DL particularly improves upon ANTS in terms of sharpness. The figure highlights the region-of-interest containing pathology and/or small features, in which the proposed algorithm preserved the details and were consistent with ANTS.Discussion and Conclusions
The results demonstrate that the proposed algorithm can effectively register between even and odd echo images, improving on the sharpness over the baseline. Large-scale training also makes it possible to train one model across all contrasts, making it suitable for the clinical deployment that can anticipate high variability in the acquired image quality. We also saw the generalization over pathology features. Future work includes directly incorporating registration to other components of the pipeline, such as image reconstruction for further image quality improvements.Acknowledgements
No acknowledgement found.References
[1] Sheth KN, Mazurek MH ,Yuen MM, Cahn BA, Shah JT, Ward A, Kim JA, Gilmore EJ, Falcone GJ, Petersen N, Gobeske KT, Kaddouh F, Hwang DY, Schindler J, Sansing L, Matouk C, Rothberg J, Sze G, Siner J, Rosen MS, Spudich S, Kimberly WT. Assessment of BrainInjury Using Portable, Low-Field Magnetic Resonance Imaging at the Bedside of Critically Ill Patients. JAMA Neurol. 2020 Sep 8 :e203263.doi:10.1001/jamaneurol.2020.3263. Epub ahead of print.PMID:32897296;PMCID:
[3] Wald LL, McDaniel PC, Witzel T, Stockmann JP, Cooley CZ. Low- cost and portable MRI. J Magn Reson Imaging. 2020;52:686- 696.
[4] Marques JP, Simonis FFJ, Webb AG. Low- field MRI: an MR physics perspective. J Magn Reson Imaging. 2019;49:1528- 1542
[5] Rearick T, Charvat G, Rosen MS, Rothberg J. Noise Suppression Methods and Apparatus. US Patent 9,797,971. March 10, 2016
[6] Schlemper J, Salehi SSM, Lazarus C, Dyvorne H, O’Halloran R, de Zwart N, Sacolick L, By S, Stein J, Rueckert D, Sofka M, Kundu P. Deep Learning MRI Reconstruction in Application to Point-of-Care MRI Proceedings of the 2020 ISMRM & SMRT Annual Meeting & Exhibition. Abstract Number 0991.
[7] Schlemper J, Dey N, Salehi SSM, Lazarus C, O’Halloran R, Kundu P, Sofka M. Unsupervised Denoising for Low-field Diffusion MRI. Proceedings of the 2021 ISMRM & SMRT Annual Meeting & Exhibition. Abstract Number 2190.
[8] Rueckert, D., Sonoda, L. I., Hayes, C., Hill, D. L., Leach, M. O., & Hawkes, D. J. (1999). Nonrigid registration using free-form deformations: application to breast MR images. IEEE transactions on medical imaging, 18(8), 712-721.
[9] Vercauteren, T., Pennec, X., Perchant, A. and Ayache, N., 2009. Diffeomorphic demons: Efficient non-parametric image registration. NeuroImage, 45(1), pp.S61-S72
[10] Avants, B. B., Tustison, N. J., Song, G., Cook, P. A., Klein, A., & Gee, J. C. (2011). A reproducible evaluation of ANTs similarity metric performance in brain image registration. Neuroimage, 54(3), 2033-2044.
[11] Balakrishnan, G., Zhao, A., Sabuncu, M.R., Guttag, J. and Dalca, A.V., 2019. Voxelmorph: a learning framework for deformable medical image registration. IEEE transactions on medical imaging, 38(8), pp.1788-1800.
[12] Dalca, A.V., Balakrishnan, G., Guttag, J. and Sabuncu, M.R., 2018, September. Unsupervised learning for fast probabilistic diffeomorphic registration. In International Conference on Medical Image Computing and Computer-Assisted Intervention (pp. 729-738). Springer, Cham.
[13] Qiu, H., Qin, C., Schuh, A., Hammernik, K., & Rueckert, D. (2021, February). Learning Diffeomorphic and Modality-invariant Registration using B-splines. In Medical Imaging with Deep Learning.
[14] Thorley, A., Jia, X., Chang, H.J., Liu, B., Bunting, K., Stoll, V., de Marvao, A., O’Regan, D.P., Gkoutos, G., Kotecha, D. and Duan, J., 2021, September. Nesterov Accelerated ADMM for Fast Diffeomorphic Image Registration. In International Conference on Medical Image Computing and Computer-Assisted Intervention (pp. 150-160). Springer, Cham.
[15] Ashburner, J., 2007. A fast diffeomorphic image registration algorithm. Neuroimage, 38(1), pp.95-113.
[16] Jaderberg, M., Simonyan, K., & Zisserman, A. (2015). Spatial transformer networks. Advances in neural information processing systems, 28, 2017-2025.
Figures