0697

Reproducibility of white matter microstructure mapping with diffusion-relaxometry

Santiago Coelho¹, Filip Szczepankiewicz², Jelle Veraart¹, Sohae Chung¹, Yvonne W. Lui¹, Dmitry S. Novikov¹, and Els Fieremans¹
¹Center for Advanced Imaging Innovation and Research (CAI2R), Department of Radiology, New York University, School of Medicine, New York, NY, United States, ²Department of Diagnostic Radiology, Clinical Sciences, Lund University, Lund, Sweden

Synopsis

Joint modeling of diffusion and relaxometry in white matter is attractive due to its potential to provide unique insights into tissue integrity. We designed a diffusion MRI protocol containing varying b-values, b-tensor shapes, and echo times, employed machine learning parameter estimation, and studied the reproducibility of the Standard Model (SM) parameters. We quantified scan-rescan reproducibility in six healthy volunteers for compartmental water fractions, diffusivities, and $$$T_2$$$ relaxation times. We also found good agreement between SM parameters obtained from diffusion-only data at fixed echo time, and those from joint diffusion-relaxometry acquisitions, providing a consistency check for the SM assumptions.

Introduction

The promise of increased sensitivity and specificity in detecting brain microstructural changes is the driving force for diffusion MRI (dMRI) modeling. In brain white matter (WM), all modeling approaches based on impermeable sticks embedded in a Gaussian extra-axonal space can be grouped under the so-called Standard Model¹, encompassing a myriad of WM models^{2,3,4,5,6,7,8}.

Recently, the SM framework has been extended for joint diffusion-relaxometry modeling^9,10,11,12, which enables separation of compartmental $$$T_2$$$ values, providing complementary microstructural information to that from dMRI at fixed TE. However, to evaluate the potential of compartmental diffusion and $$$T_2$$$-parameters as candidate diagnostic or surrogate markers in disease, we need robust and reproducible estimation. Here, we address this often overlooked aspect.

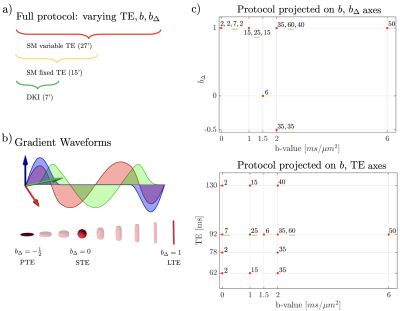
Unconstrained estimation of SM parameters has shown to be ill-conditioned^8,13 unless strong diffusion weightings or orthogonal measurements are acquired^14,15, as shown experimentally^9,11,16. We propose an optimized dMRI protocol that leverages multiple diffusion weightings ($$$b$$$), tensor encodings ($$$b_\Delta$$$), and echo times (TE), with subsets that allow for SM estimation for fixed TE, as well as DKI. Six healthy volunteers were recruited to evaluate scan-rescan reproducibility of diffusion-relaxometry white matter modeling on a clinical scanner. We show not only reproducible results but also good agreement between joint diffusion-relaxometry modeling and diffusion-only modeling.

Theory

Multidimensional dMRI measurements generalize the scalar b-value (one-dimensional diffusion-weighting) to a b-tensor $$$\boldsymbol{B}$$$¹⁷. We consider axially symmetric b-tensors, $$$B_{ij}=b(b_\Delta n_in_j+\frac{1-b_\Delta}{3}\delta_{ij})$$$, where $$$b=\mathrm{tr}\,\boldsymbol{B}$$$ is the b-value, $$$\mathbf{\hat{n}}$$$ the orientation, and $$$b_\Delta$$$ parametrizes b-tensor shape, e.g. $$$b_\Delta=1, 0, -\tfrac{1}{2}$$$ for linear, spherical, or planar tensor encoding, respectively. This extends the acquisition space and each shell is defined by a pair $$$(b,b_\Delta)$$$. Adequately sampling the ($$$b,b_\Delta$$$) acquisition space has been shown sufficient for well-conditioned SM parameter estimation^14,15.
The Standard Model signal is the spherical convolution¹ of the fibers' orientation distribution function (ODF) $$$\mathcal{P}(\hat{\mathbf{u}})$$$ and the response signal of a fiber segment $$$\mathcal{K}$$$. Extending it to tensor-valued diffusion encoding and varying echo times means each compartment is assigned a specific $$$T_2$$$ relaxation time^9,11:$$\begin{aligned}S(\boldsymbol{B},\text{TE})&=s_0\int_{\mathbb{S}^2}\mathcal{P}(\hat{\mathbf{u}})\mathcal{K}(\boldsymbol{B},\text{TE},\hat{\mathbf{u}})\,d\hat{\mathbf{u}},\\\text{where}\,\mathcal{K}(\boldsymbol{B},\text{TE},\hat{\mathbf{u}})&=f\exp\bigl[-D_{\text{a}}\sum_{ij}B_{ij}u_iu_j-\text{TE}/T_{2,\text{a}}\bigr]\\&+(1-f-f_\text{FW})\exp\bigl[-bD_\text{e}^\perp-(D_\text{e}^\parallel-D_\text{e}^\perp)\sum_{ij}B_{ij}u_i u_j-\text{TE}/T_{2,\text{e}}\bigr]\\&+ f_\text{FW}\exp\bigl[-bD_\text{FW}-\text{TE}/T_{2,\text{FW}}\bigr]\end{aligned}$$and $$$\hat{\mathbf{u}}$$$ is the fiber segment orientation. $$$f$$$ and $$$f_\text{FW}$$$ are the intra-axonal and free-water signal fractions. $$$D_{\text{a}}$$$, $$$D_\text{e}^\parallel$$$, $$$D_\text{e}^\perp$$$, and $$$D_\text{FW}$$$ are the axial intra-axonal, axial extra-axonal, radial extra-axonal, and free-water diffusivities, respectively; $$$T_{2,\text{a}}$$$, $$$T_{2,\text{e}}$$$, and $$$T_{2,\text{FW}}$$$ are the compartment-specific relaxation times.We use $$$p_2$$$, the $$$\ell=2$$$ ODF rotational invariant, to quantify anisotropy ($$$p_2=1$$$ for parallel fibers, $$$p_2=0$$$ for isotropically distributed fibers).

Methods

Imaging. After informed consent, six healthy volunteers (24-52yo, 3female-3male) underwent brain MRI on a 3T Siemens Prisma, using a 64-channel head coil. The dMRI protocol consisted of Maxwell-compensated asymmetric waveforms¹⁸ with isotropically distributed orientations at varying ($$$b,b_\Delta,$$$TE) combinations shown in Fig. 1. A non-diffusion-weighted image with reverse phase-encoding was acquired to correct for EPI-induced distortions¹⁹. Imaging parameters: voxel size$$$=2\times2\times2\,$$$mm$$$^3$$$, $$$T_R\geq4s$$$, bandwidth=1818Hz/Px, $$$R_\text{GRAPPA}=2$$$, partial Fourier = 6/8. Subjects were scanned and subsequently rescanned with the same dMRI protocol, with repositioning in-between.The dMRI data was denoised^20,21, corrected for Gibbs artifacts²², and for eddy current distortions and subject motion simultaneously²³. Coefficients of variation (COV) were computed from the two repetitions. The full multi $$$b,b_\Delta,$$$TE protocol ($$$t_\text{acq}=27'$$$) was used to jointly estimate the diffusion-relaxometry SM parameters. A subset of this protocol acquired at TE$$$=92$$$ms ($$$t_\text{acq}=15'$$$) was used for estimating fixed-TE SM parameters. A further subset was used for DKI estimation. To compare results between variable-TE and fixed-TE protocols, we weigh the variable-TE fractions with corresponding $$$e^{-\mathrm{TE}/T_2}$$$ factors, and rescale them to sum to 1.
Parameter estimation was done using a supervised machine learning method based on polynomial regression from the rotational invariants²⁴. This has been shown to minimize estimation error for typical signal-to-noise ratios on in vivo data²⁵. Training data was generated from a wide distribution on the physically plausible range without constraints.

Results

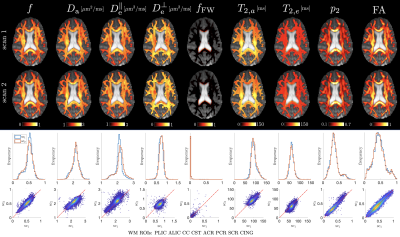
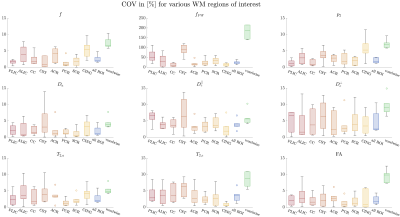
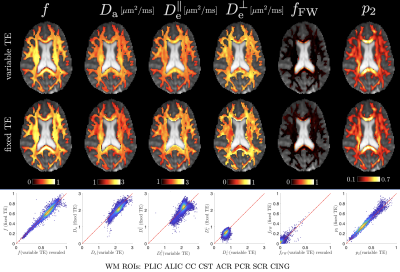
Representative WM parametric maps are shown in Fig. 2 for a 28yo male subject, along with histograms and scatter plots over multiple regions of interest. The COV between scans for each SM parameter and fractional anisotropy from a DKI estimation are shown in Fig 3. ROI means had COV between $$$2-4\%$$$ while voxelwise COVs were in the range $$$5-10\%$$$.
We found high agreement between SM parameters obtained from fixed-TE and variable-TE acquisitions (see maps and scatter plots in Fig. 4). This provides a consistency check for the SM assumptions.

Discussion and Conclusions

We proposed a multi-$$$b,b_\Delta,$$$TE protocol for estimating compartmental diffusion and relaxation SM parameters and assessed their reproducibility. Supervised machine learning parameter estimation was used to improve precision. Our water fractions from the full protocol yielded reasonable estimates, showing higher $$$f$$$ values in densely packed tracts and negligible free-water fraction $$$f_\text{FW}$$$ throughout the WM except in voxels adjacent to the ventricles. Compartmental $$$T_2$$$ values were in good agreement with^9,26, showing $$$T_{2,\text{a}}>T_{2,\text{e}}$$$. Our $$$D_\text{a}$$$ estimates agreed with^27,28 but were slightly lower than those reported in^29,30. The scan-rescan reproducibility of SM parameters was comparable to that of FA, which is encouraging and points to the feasibility of robustly recovering diffusion and relaxometry properties. Finally, parameter estimates from the fixed-TE protocol subset were in close agreement with the prediction from the variable-TE full protocol. This agreement between modeling approaches suggests that with a comprehensive experiment design the SM accurately captures the signal content in the diffusion signal.

Acknowledgements

This work has been supported by NIH under NINDS award R01 NS088040 and R01 NS119767-01A1 and NIBIB awards R01 EB027075 and P41 EB017183.

References

1. D. S. Novikov, E. Fieremans, S. N. Jespersen, and V. G. Kiselev, “Quantifying brain microstructure with diffusion MRI: Theory and parameter estimation,” NMR in Biomedicine, p. e3998, 2019.

2. C. D. Kroenke, J. J. Ackerman, and D. A. Yablonskiy, “On the nature of the naa diffusion attenuated mr signal in the central nervous system,” Magnetic Resonance in Medicine, vol. 52, no. 5, pp. 1052–1059, 2004.

3. Y. Assaf, T. Blumenfeld-Katzir, Y. Yovel, and P. J. Basser, “New modeling and experimental framework to characterize hindered and restricted water diffusion in brain white matter,” Magnetic Resonance in Medicine, vol. 52, pp. 965–978, 2004.

4. S. N. Jespersen, C. D. Kroenke, L. Østergaard, J. J. H. Ackerman, and D. A. Yablonskiy, “Modeling dendrite density from magnetic resonance diffusion measurements,” NeuroImage, vol. 34, pp. 1473–1486, 2007.

5. E. Fieremans, J. H. Jensen, J. A. H. ans Sungheon Kim, R. I. Grossman, M. Inglese, and D. S. Novikov, “Diffusion distinguishes between axonal loss and demyelination in brain white matter,” in Proceedings of the International Society of Magnetic Resonance in Medicine, Wiley, 2012.

6. H. Zhang, T. Schneider, C. A. Wheeler-Kingshott, and D. C. Alexander, “NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain,” NeuroImage, vol. 61, pp. 1000–1016, 2012.

7. J. H. Jensen, G. Russell Glenn, and J. A. Helpern, “Fiber ball imaging,” NeuroImage, vol. 124, pp. 824–833, 2016.

8. D. S. Novikov, J. Veraart, I. O. Jelescu, and E. Fieremans, “Rotationally-invariant mapping of scalar and orien- tational metrics of neuronal microstructure with diffusion MRI,” NeuroImage, vol. 174, pp. 518 – 538, 2018.

9. J. Veraart, D. S. Novikov, and E. Fieremans, “TE dependent Diffusion Imaging (TEdDI) distinguishes between compartmental T2 relaxation times,” NeuroImage, vol. 182, pp. 360–369, 2017.

10. E. T. McKinnon and J. H. Jensen, “Measuring intra-axonal t2 in white matter with direction-averaged diffusion mri,” Magnetic Resonance in Medicine, vol. 81, no. 5, pp. 2985–2994, 2019.

11. B. Lampinen, F. Szczepankiewicz, J. M ̊artensson, D. van Westen, O. Hansson, C.-F. Westin, and M. Nilsson, “Towards unconstrained compartment modeling in white matter using diffusion-relaxation mri with tensor-valued diffusion encoding,” Magnetic Resonance in Medicine, vol. 84, no. 3, pp. 1605–1623, 2020.

12. T. Gong, Q. Tong, H. He, Y. Sun, J. Zhong, and H. Zhang, “Mte-noddi: Multi-te noddi for disentangling non- t2-weighted signal fractions from compartment-specific t2 relaxation times,” NeuroImage, vol. 217, p. 116906, 2020.

13. I. O. Jelescu, J. Veraart, E. Fieremans, and D. S. Novikov, “Degeneracy in model parameter estimation for multi-compartmental diffusion in neuronal tissue,” NMR in Biomedicine, vol. 29, pp. 33–47, 2016.

14. S. Coelho, J. M. Pozo, S. N. Jespersen, D. K. Jones, and A. F. Frangi, “Resolving degeneracy in diffusion MRI biophysical model parameter estimation using double diffusion encoding,” Magnetic Resonance in Medicine, vol. 82, pp. 395–410, 2019.

15. M. Reisert, V. G. Kiselev, and B. Dhital, “A unique analytical solution of the white matter standard model using linear and planar encodings,” Magnetic Resonance in Medicine, vol. 81, pp. 3819–3825, 2019.

16. S. Coelho, J. M. Pozo, S. N. Jespersen, and A. F. Frangi, “Optimal experimental design for biophysical modelling in multidimensional diffusion MRI,” in Medical Image Computing and Computer-Assisted Intervention (MICCAI), vol. 3542, Springer, 2019.

17. C.-F.Westin,H.Knutsson,O.Pasternak,F.Szczepankiewicz,E.O ̈zarslan,D.vanWesten,C.Mattisson,M.Bo- gren, L. J. O’Donnell, M. Kubicki, D. Topgaard, and M. Nilsson, “q-space trajectory imaging for multidimensional diffusion MRI of the human brain,” NeuroImage, vol. 135, pp. 345–362, 2016.

18. F. Szczepankiewicz, C.-F. Westin, and M. Nilsson, “Maxwell-compensated design of asymmetric gradient wave- forms for tensor-valued diffusion encoding,” Magnetic Resonance in Medicine, vol. 0, pp. 1–14, 2019.

19. J. L. Andersson, S. Skare, and J. Ashburner, “How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging,” NeuroImage, vol. 20, no. 2, pp. 870–888, 2003. 8

20. J. Veraart, E. Fieremans, and D. S. Novikov, “Diffusion MRI noise mapping using random matrix theory,” Magnetic Resonance in Medicine, vol. 76, no. 5, pp. 1582–1593, 2016.

21. L. Cordero-Grande, D. Christiaens, J. Hutter, A. N. Price, and J. V. Hajnal, “Complex diffusion-weighted image estimation via matrix recovery under general noise models,” NeuroImage, vol. 200, pp. 391–404, 2019.

22. H.-H. Lee, D. S. Novikov, and E. Fieremans, “Removal of partial fourier-induced gibbs (rpg) ringing artifacts in mri,” Magnetic Resonance in Medicine, vol. 86, no. 5, pp. 2733–2750, 2021.

23. S. M. Smith, M. Jenkinson, M. W Woolrich, C. F Beckmann, T. E J Behrens, H. Johansen-Berg, P. Bannister, M. Luca, I. Drobnjak, D. Flitney, R. Niazy, J. Saunders, J. Vickers, Y. Zhang, N. De Stefano, M. Brady, and P. Matthews, “Advances in functional and structural mr image analysis and implementation as fsl,” NeuroImage, vol. 23 Suppl 1, pp. S208–19, 02 2004.

24. M. Reisert, E. Kellner, B. Dhital, J. Hennig, and V. G. Kiselev, “Disentangling micro from mesostructure by diffusion MRI: A Bayesian approach,” NeuroImage, vol. 147, pp. 964 – 975, 2017.

25. S. Coelho, E. Fieremans, and D. S. Novikov, “How do we know we measure tissue parameters, not the prior?,” in Proceedings of the International Society of Magnetic Resonance in Medicine, Wiley, 2021.

26. J. P. de Almeida Martins, M. Nilsson, B. Lampinen, M. Palombo, P. T. While, C.-F. Westin, and F. Szczepankiewicz, “Neural networks for parameter estimation in microstructural mri: Application to a diffusion- relaxation model of white matter,” NeuroImage, vol. 244, p. 118601, 2021.

27. J. Veraart, E. Fieremans, and D. S. Novikov, “On the scaling behavior of water diffusion in human brain white matter,” NeuroImage, vol. 185, pp. 379–387, 2019.

28. B. Dhital, M. Reisert, E. Kellner, and V. G. Kiselev, “Diffusion weighting with linear and planar encoding solves degeneracy in parameter estimation,” in Proceedings of the International Society of Magnetic Resonance in Medicine, Wiley, 2018.

29. A. F. Howard, F. J. Lange, J. Mollink, M. Cottaar, M. Drakesmith, S. Umesh Rudrapatna, D. K. Jones, K. L. Miller, and S. Jbabdi, “Estimating intra-axonal axial diffusivity in the presence of fibre orientation dispersion,” bioRxiv, 2020.

30. M. Nilsson, S. St-Jean, C. Beaulieu, and F. Szczepankiewicz, “Estimation of intra-axonal axial diffusivity by tensor-valued dmri and powder-averaging,” in Proceedings of the International Society of Magnetic Resonance in Medicine, vol. 0647, Wiley, 2021.

Figures

Figure 1 a) Description of the scan protocol together with the subsets. b) Schematic representation of diffusion waveforms and b-tensors. c) Diagram of the full protocol. Each shell, defined by ($$$b,b_\Delta,\text{TE},N_\text{dirs}$$$), is denoted with a red dot and plotted in two different projections with the number of isotropically distributed directions next to it. When two shells have an identical projection the number of directions are separated by commas. The fixed TE subset of the protocol is underlined in yellow, and a further DKI subset is underlined in green.

Figure 2 Columns show different SM and fractional anisotropy maps for a healthy volunteer (28-year-old male). The first two rows contain color maps showing WM voxels plotted on top of a $$$T_2$$$-weighted image. These rows contains estimates from two identical scans. The third and fourth rows contain histograms and scan1-scan2 scatter plots comparing estimates from voxels belonging to the main WM regions of interest.

Figure 3 Coefficients of variation (COV$$$=\sigma/\mu$$$) for all diffusion+relaxometry SM parameters and FA (computed from the DKI shells). The mean and standard deviation were estimated as: $$$\hat{\mu}=\tfrac12(x_1+x_2),\,\hat{\sigma} = \tfrac{\sqrt{\pi}}{2}|x_1-x_2|$$$.The COV is shown for different white matter regions of interest (ROI), for the weighted average over all ROIs, and the voxelwise COV is added for reference. Note that free water fraction values are very small so relative voxelwise errors are very large.

Figure 4 Comparison of SM maps between the variable-TE (diffusion+relaxometry) and the fixed-TE (diffusion only) for a healthy volunteer (28-year-old male). The SM framework is essentially the same between fixed-TE and variable-TE acquisitions; the added value of compartmental $$$T_2$$$-times is to provide additional contrasts and remove the $$$T_2$$$-weighting on the fixed-TE fraction estimates. Water fractions, $$$f$$$ and $$$f_\text{FW}$$$, from the variable-TE protocol were adjusted to be compatible with the fixed-TE protocol as described in the main text.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

0697

DOI: https://doi.org/10.58530/2022/0697