Introduction

In this work, we investigate model pruning to reduce deep learning model overfitting, by targeted removal of parameters during the training process. This is important since semantic segmentation in medical imaging is vital for understanding and monitoring disease progression, but manual segmentation is time consuming and difficult (e.g. due to ambiguous structure boundaries, reducing consistency of different raters). Therefore, reliable and accurate automatic segmentation methods are needed and deep learning-based methods are the state-of-the-art for medical image segmentation. Most methods are based on the UNet architecture¹, but without very large numbers of manual segmentations for training, these models overfit to the training data, leading to poor performance, especially when applied to data from different distributions (e.g. data from different MRI scanners or acquired with different protocols). A primary cause of this overfitting is the vast number of parameters in such convolutional neural networks (CNNs), and our pruning approach aims to tackle this problem.

Methods

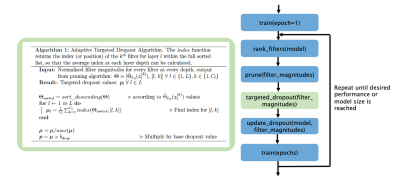
We propose the TrainPrune + Targeted Dropout (TD) algorithm (Fig. 1), a novel approach aiming to prune and train a model simultaneously. Consider the scenario where there is access to a training dataset $$$D =\{\mathbf{X}=\{ \mathbf{x}_1,\mathbf{x}_2...\mathbf{x}_N\},\mathbf{Y}=\{ \mathbf{y}_1,\mathbf{y}_2...\mathbf{y}_N\}\}$$$ where $$$\mathbf{x}_n\in {R}^{W\times H\times D\times1}$$$ represents an input image and $$$\mathbf{y}_n\in {R}^{W\times H\times D\times C}$$$ is the corresponding target segmentation with $$$C$$$ classes. A network is trained to predict the target segmentations from the input images, and is parameterized by $$${W}=\{(\mathbf{w}_1^1,b_1^1),(\mathbf{w}_1^2,b_1^2),...(\mathbf{w}_L^{C_L},b_L^{C_L})\}$$$ where $$$\mathbf{w}_m^n$$$ and $$$b_m^n$$$ correspond to the weights and biases for the n^th filter of the m^th layer, and $$$C_L$$$ is the number of channels in layer $$$L$$$. The weights and biases (represented jointly by $$$W$$$) are first randomly initialized and optimized to minimize $$$L(D|W)$$$. The aim of the pruning process is to refine the parameters, $$$W$$$, of the network to a smaller subset, $$$W'$$$, such that $$$L(D|W)\approx L(D|W')$$$.
We prune whole convolutional filters² and, to decide which features to remove, we consider the feature activation maps, $$$\mathbf{z}_l^{(k)}=ReLU(\mathbf{z}_{(l - 1)}*\mathbf{w}_l^{(k)}+b_l^{(k)})$$$ where ReLU is the activation function used throughout the network. The weights with the smallest impact on the final prediction are those with the smallest average magnitudes³; thus the weights and biases corresponding to the smallest magnitude filter activations $$$\mathbf{z}_{l}^{(k)}$$$, averaged over the training data, are removed. To assess the magnitude of the filters, the L₂-norm is used as it is computationally simple and provides stable performance: $$$\Theta_{L_2}(\mathbf{z}_l^{(k)})=\frac{1}{N}\sum^N_{i=1}{||\;\mathbf{z}_{l,i}^{(k)}\;||}_2$$$. These values are then normalised across the layer depth using L2 normalisation, $$$\hat{\Theta}_{L_2}(\mathbf{z}_l^{(k)})=\frac{\Theta_{L_2}(\mathbf{z}_l^{(k)})}{\sqrt{\sum_j (\Theta_{L_2}(\mathbf{z}_j^{(k)}))^2 }}$$$, to account for values being different at different scales and depths².
To make the model robust via pruning, we introduce adaptive channelwise targeted dropout, where the dropout probability is based on the average index of the filters, ordered by magnitude at a given depth (Algorithm 1, Fig. 1). Thus, the filters with the lowest magnitude have the highest dropout probability, and so are more likely to be removed during training. As we are pruning channelwise, spatial dropout⁴ is applied.
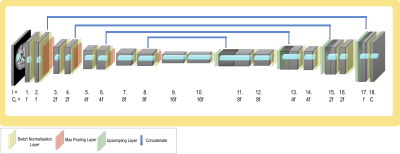
To explore the effect of pruning on model generalisability, we consider T1 data from three sites in the ABIDE dataset⁵. As manual segmentation labels are not available, we created proxy labels using FSL FAST⁶, creating tissue segmentations (C=4). Data from the UM site was used for training; the performance was tested on a held-out test set (UM), and two unseen sites: Yale (similar age profile) and MPG (significantly different age profile). A standard 3D UNet architecture⁷ was considered (Fig. 2), as it is the architecture most commonly used in medical image segmentation. We compare our proposed TrainPruneTD approach to a Standard UNet approach. Across the experiments, 2 epochs of training were completed between each filter pruning, and $$$b_{drop}$$$ (the dropout probability scaling factor) was set to 0.05 in all cases. The number of filters in the first layer, f, was set to 4 unless otherwise specified, and all layers but the final, $$$l=18$$$ layer, were subject to pruning.

Results and Discussion

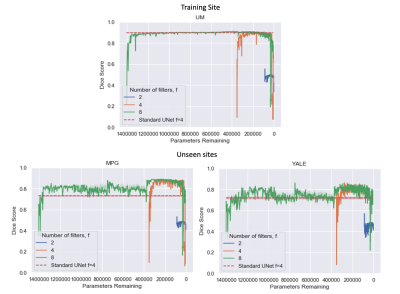
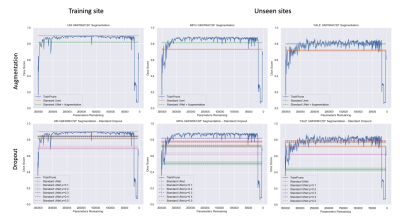
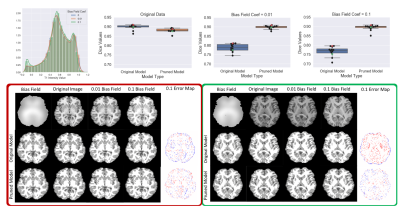
Figure 3 shows the results comparing TrainPruneTD to Standard UNet, for different initial model architecture sizes. It is clear that we can prune models greatly without decreasing the performance on the task. Critically, it clearly shows that pruning increases the performance on the two unseen sites compared to the Standard UNet, improving the generalisability of the model.
Figure 4 shows the results for $$$f=4$$$, comparing TrainPruneTD to the Standard UNet with and without augmentation⁸ during training, to simulate changes expected between sites. The TrainPruneTD model still outperforms the Standard UNet on the two unseen sites, indicating that although augmentation can increase generalisability for these models, our pruning approach does not explicitly require the identification of all the likely changes between sites. The same result was also seen comparing TrainPruneTD to standard dropout⁹, with TrainPruneTD generalising better across the sites. The performance of the TrainPruneTD and Standard UNet approaches for increasing levels of applied bias field⁸ (Fig. 5) further demonstrate improved generalisability as TrainPruneTD is more robust to such intensity-based changes.
These results clearly demonstrate that pruning during training can increase the generalisability of CNN based models and, thus, their applicability to multisite MRI data, and the flexible algorithm should be applicable across tasks and architectures.

Acknowledgements

ND is supported by the Engineering and Physical Sciences Research Council (EPSRC) and Medical Research Council (MRC) [grant number EP/L016052/1]. MJ is supported by the National Institute for Health Research (NIHR), Oxford Biomedical Research Centre (BRC), and this research was funded by the Wellcome Trust [215573/Z/19/Z]. The Wellcome Centre for Integrative Neuroimaging is supported by core funding from the Wellcome Trust [203139/Z/16/Z]. AN is grateful for support from the UK Royal Academy of Engineering under the Engineering for Development Research Fellowships scheme. The computational aspects of this research were supported by the Wellcome Trust Core Award [Grant Number 203141/Z/16/Z] and the NIHR Oxford BRC. The views expressed are those of the author(s) and not necessarily those of the NHS, the NIHR or the Department of Health.