0685
Uncertainty estimation via ensembling for deep learning-based MR image reconstruction
Tobias Hepp1,2, Sergios Gatidis1,2, Kerstin Hammernik3,4, and Thomas Küstner1
1Medical Image and Data Analysis (MIDAS.lab), Department of Diagnostic and Interventional Radiology, University Hospital of Tuebingen, Tübingen, Germany, 2Max Planck Institute for Intelligent Systems, Tübingen, Germany, 3Lab for AI in Medicine, Technical University of Munich, Munich, Germany, 4Department of Computing, Imperial College London, London, United Kingdom
1Medical Image and Data Analysis (MIDAS.lab), Department of Diagnostic and Interventional Radiology, University Hospital of Tuebingen, Tübingen, Germany, 2Max Planck Institute for Intelligent Systems, Tübingen, Germany, 3Lab for AI in Medicine, Technical University of Munich, Munich, Germany, 4Department of Computing, Imperial College London, London, United Kingdom
Synopsis
Deep learning-based MR image reconstruction from undersampled data bears the risk of inducing reconstruction errors like in-painting of non-anatomical structures, or missing pathologies. These errors may be obscured by the deep learning process and thus remain undiscovered. Furthermore, most methods are task-specialized and not well calibrated to domain shifts. Thus, integrated uncertainty prediction would be desirable. We propose a deep ensembling strategy that allows us to assess potential algorithm failures and better adapt to changing scenarios. The proposed approach can be paired with any DL reconstruction, enabling investigations of their predictive uncertainties on a voxel-level.
Introduction
The development of artificial intelligence has evolved tremendously during the last decade and is likely to transform clinical workflow in the coming years fundamentally. In particular for MRI, we have seen several advances in the last years to accelerate MR imaging. The proposed deep learning (DL)-based reconstruction methods enabled shorter scan times and/or improved spatial/temporal resolution while reducing aliasing artifacts. Image enhancement1-3, physics-based unrolled networks4-7, k-space learning8,9, transform learning10 and hybrid learning11,12 networks have been proposed.However, image reconstruction from undersampled data bears the risk of reconstruction errors that may be obscured by the DL process and thus remain undiscovered. Furthermore, most methods are task-specialized and not well calibrated to domain shifts of imaging sequences, contrasts, accelerations, examined body region or subjects (healthy volunteers vs. patients). DL-based reconstructions also still elicit the anxiety of risking to in-paint non-anatomical structures or to miss pathologies13. A further major challenge in these DL-based solutions is the interpretation of predictions and the creation of visual explanations.
To address these challenges, we aim to introduce measures of predictive uncertainty in the DL-based reconstruction process that allow for transparent assessment of potential algorithm failure and to better adapt for changing scenarios. While aleatoric uncertainty aims to model in-distribution noise due to noisy ground truth labels, epistemic uncertainty focuses on the uncertainty in the model parameters itself, which are in practice always derived from a limited number of training samples. A variety of methods have been developed for quantifying predictive uncertainty, including maximum softmax probability14, temperature scaling15, Monte-Carlo dropout16, ensembling17 or stochastic variational Bayesian inference18-20.
We propose in this work to predict epistemic uncertainties in DL-based MR reconstructions via ensemble techniques17 which have been shown to be well suited for out-of-distribution uncertainty quantification in the context of DL models21,22. The proposed approach can be paired with any type of DL reconstruction, enabling investigations of their prediction uncertainties on a voxel-level. The obtained uncertainty maps provide thus an interpretable solution to examine epistemic uncertainties in relation to the underlying anatomical structures.
Methods
In contrast to a full Bayesian treatment, i.e. modeling the posterior distribution over the network parameters given the training data, ensembling allows for a more convenient and simplistic implementation of predictive uncertainty21,22. Computing the full posterior requires knowledge about a prior distribution and an approximation strategy to implement the otherwise intractable true posterior. With deep ensembles we produce samples directly from a distribution over the network weights based on the major sources of randomness during the optimization process: weight initialization and batch sampling. This can be regarded as the posterior distribution to an implicitly assumed yet explicitly unknown prior. Moments of the predictive distribution, including a notion of uncertainty, can then be derived using Monte-Carlo (MC) simulation23.A deep ensemble with five different random seeds for initialization and batching is used. The mean and standard deviation of the predictive distribution is MC-approximated using the predictions of the ensemble members as samples which is illustrated in Fig.1. A UNet-based image enhancement network with two levels in encoder/decoder and two convolutional layers (3$$$\times$$$3 kernel size, 32 base features), ReLU activation and instance normalization per level was investigated. The network was trained with ADAM (learning rate 10-3, batch size 8) over 200 epochs to minimize the mean squared error loss.
Under the assumption of sufficient independent labeled samples respectively fully-sampled reference from a target data distribution, the alignment of a model's confidence with its accuracy can be estimated and used to adjust the predictions accordingly. We therefore studied the effects on independent and identically distributed data samples from the fastMRI database24 with known fully-sampled references. Coronal single-coil proton-density weighted knee data without (267 patients) and with fat-saturation (269 patients) of the TSE sequence24 were used. Fully-sampled data was used as target reference, and retrospectively undersampled with acceleration factors R=4,8 for fully-sampled central regions of 4% (small), 8% (medium) and 16% (large) size, resulting in 7504/3471 training/test slices.
Results and Discussion
Fig.2 shows exemplary uncertainty predictions in two test subjects for changing fully-sampled centers. The highest uncertainty was obtained on edges and sharp boundaries like periosteum or collateral ligaments, i.e. at areas of lost high-frequency information due to undersampling. Reduced fully-sampled centers resulted in overall increased uncertainty. For sufficiently large fully-sampled centers, uncertainties primarily arise from aliasing artifacts. For higher accelerations as shown in Fig.3 stronger uncertainty bands along medial-lateral direction are observed. For increasing accelerations and larger aliasing artifact impact (i.e. small fully-sampled center), the networks showed an increased uncertainty. Average reconstruction errors and predictive uncertainty are well correlated in all investigated scenarios (Fig.4+5), i.e. larger reconstruction errors resulted in larger predictive uncertainties.This study has some limitations. We only investigated the proposed approach in single-coil data and of a single imaging sequence and contrast. In the future, we plan to extend it to examine out-of-distribution data (i.e. subjects with pathologies which were not seen during training) and to deploy calibration methods that optimize the quantitative fidelity of uncertainty estimates to strengthen against domain shifts. Furthermore, the intrinsic uncertainties of different reconstruction architectures will be examined.
Conclusion
The proposed approach enables epistemic uncertainty prediction for DL-based MR reconstruction with an interpretable examination on voxel-level.Acknowledgements
This project was supported by the Germany’s Excellence Strategy – EXC-Number 2064/1 – Project number 390727645 and EXC-Number 2180 – Project number 390900677.References
1. Hauptmann et al. Magn Reson Med 2019;81.2. Kofler et al. IEEE Transactions on Medical Imaging 2020;39(3).
3. Lee et al. IEEE Transactions on Biomedical Engineering 2018;65(9).
4. Schlemper et al. IEEE Transactions on Medical Imaging 2018;37.
5. Aggarwal et al. IEEE Transactions on Medical Imaging 2019;38(2).
6. Hammernik et al. Magn Reson Med 2017(6).
7. Küstner et al. Sci Rep 2020;10.
8. Lee et al. Magn Reson Med 2016;76.
9. Akçakaya et al. Magn Reson Med 2019;81.
10. Zhu et al. Nature 2018;555(7697).
11. Eo et al. Magn Reson Med 2018;80(5).
12. El-Rewaidy et al. Magn Reson Med 2021;85(3).
13. Antun et al. Proceedings of the National Academy of Sciences 2020;117(48).
14. Hendrycks et al. arXiv preprint arXiv:161002136 2016.
15. Guo et al. International Conference on Machine Learning 2017. p1321-30.
16. Gal et al. International Conference on Machine Learning 2016. p1050-9.
17. Lakshminarayanan et al. arXiv preprint arXiv:161201474 2016.
18. Graves. Advances in Neural Information Processing Systems 2011;24.
19. Blundell et al. International Conference on Machine Learning 2015. p1613-22.
20. Narnhofer et al. IEEE Transactions on Medical Imaging 2021.
21. Ovadia et al. arXiv preprint arXiv:190602530 2019.
22. Ashukha et al. arXiv preprint arXiv:200206470 2020.
23. Bishop. Pattern Recognition and Machine Learning (Information Science and Statistics): Springer-Verlag; 2006.
24. Zbontar et al. arXiv preprint arXiv:181108839 2018.
Figures
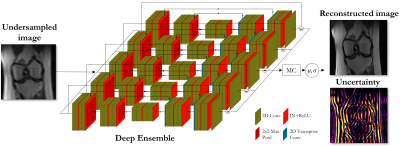
Fig. 1: Proposed deep ensemble strategy to predict epistemic uncertainty of deep learning-based MR reconstruction. Reconstruction networks were trained with different random seeds. Monte carlo approximation for the moments of the predictive distribution which uses the predictions of all ensemble members yields then the predictive uncertainty.
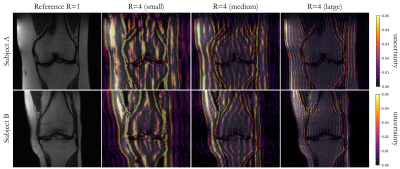
Fig. 2: Predictive uncertainty in two subjects (rows) of investigated deep ensemble strategy with UNet reconstruction. Fully-sampled reference (R=1) and reconstructed images overlaid with epistemic uncertainty are depicted for an acceleration of R=4 and changing fully-sampled central region of 4% (small), 8% (medium) and 16% (large).

Fig. 3: Predictive uncertainty in two subjects (rows) of investigated deep ensemble strategy with UNet reconstruction. Fully-sampled reference (R=1) and reconstructed images overlaid with epistemic uncertainty are depicted for an acceleration of R=4 in comparison to an acceleration of R=8 for a fully-sampled central region of 8% (medium).
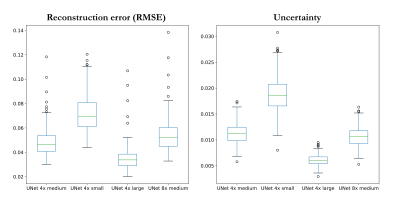
Fig. 4: Quantitative analysis of root mean squared error (RMSE) reconstruction error and predictive epistemic uncertainty over all test subjects for different accelerations R=4/R=8 and fully-sampled central region of 4% (small), 8% (medium) and 16% (large). Boxplots depict the median (horizontal line), 25% and 75% quantile (boxes), standard deviation (whiskers) and outliers (circles).
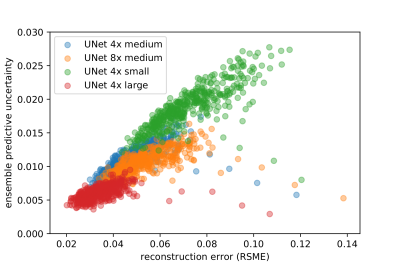
Fig. 5: Predictive uncertainty over root mean squared error (RMSE) reconstruction error for investigated deep ensemble strategy with UNet reconstruction in all test subjects for different accelerations R=4/R=8 and fully-sampled central region of 4% (small), 8% (medium) and 16% (large).
DOI: https://doi.org/10.58530/2022/0685