Purpose/Introduction

The reduced echo time in ultra-short echo time (UTE) radial 3D MRI methods significantly reduce the $$$T_2^*$$$ losses in the lung, enabling the imaging of fine structures within the lung; the non-iodizing nature of MR imaging and the ability to image lung function makes this approach desirable over competing methods. The main challenge in high-resolution pulmonary applications is the respiratory motion; the breath-hold duration severely restricts the resolution in 3D applications. Free-breathing imaging using self-gating, which bin the radial data to different respiratory bins, has recently shown to be a promising alternative [1]. However, a limitation of the self-gating approach is its dependence on assumed periodic tidal breathing that makes it sensitive to blurring due to bulk motion and unable to capture dynamic respiratory motion.

The main focus of this abstract is to introduce a novel manifold learning approach for motion compensated dynamic lung MRI. Deep manifold learning schemes have been recently introduced for motion-resolved dynamic MRI, which have conceptual similarities with self-gating approaches [2]. The main distinction of this work is the generalization to the motion compensated setting. By enabling the combination of data from different motion phases, this approach can significantly improve the image quality compared to the self-gating and previous manifold methods. More importantly, this approach is robust to bulk motion during the scans, which is a challenge with gating based methods. This approach recovers the dynamic time series, which enables the functional lung imaging, facilitating the estimation of lung and vessel contraction and diaphragm motion.

Methods

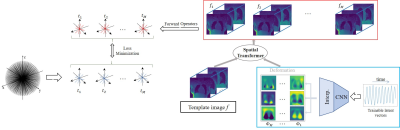
The deformation fields at different time instants, denoted by $$$\Phi_t$$$, are assumed to lie on a smooth manifold; the fields are modeled as the output of a deep convolutional neural network (CNN) $$$\mathcal{G}_{\theta}$$$ whose weights are denoted by $$$\theta$$$ in response to a low-dimensional time varying latent vector $$\Phi_t = \mathcal{G}_{\theta}(\mathbf z_t).$$ Each image in the time series $$$f_t$$$ is assumed to be derived from an image volume $$$f$$$, deformed by the above motion fields (see Fig 1) as $${f}_t = \mathcal{D}(f, \mathcal{G}_{\theta}(\mathbf{z}_t));$$ here $$$\mathcal D$$$ is an interpolation layer. The parameters of the CNN $$$\theta$$$, the image $$$f$$$, and the latent vectors $$$\mathbf{z}_t$$$ are jointly learned from the measured data of each subject in an unsupervised fashion by minimizing:
$$\mathcal{C}(\mathbf{z},\theta,{f}) = \sum_{t=1}^M||\mathcal{A}_t({f}_t)-\mathbf{b}_t||^2 + \lambda_t||\nabla_t\mathbf{z}_t||.$$
Here, $$$\mathcal{A}_t$$$ are the multichannel non-uniform FFT forward models for the time point $$$t$$$, while $$$\mathbf b_t$$$ are the corresponding measurements. Note that we also add a smoothness penalty on the latent vector $$$\mathbf{z}$$$ along the time direction to encourage the latent vectors to be smooth.

Post-learning, the image volume at each time instance is recovered as the deformed version of the fixed volume, using the motion field derived from the CNN using the corresponding latent vector.

Results

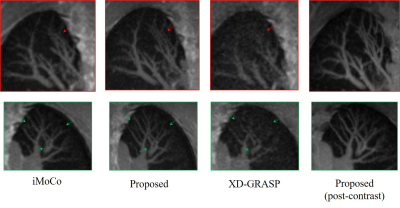
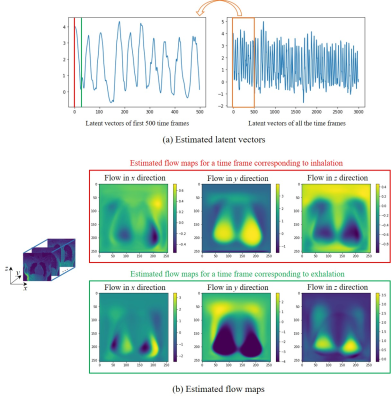
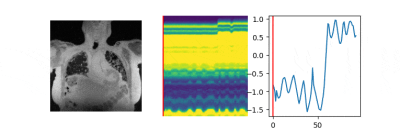
The data are acquired on a GE 3T scanner with a 3D radial UTE sequence with variable density readouts to oversample the center of k-space and bit-reversed view ordering with 32 channels. Pre and post-contrast datasets were acquired from a healthy volunteer and a patient with fibrosis. The data was acquired with 90K radial spokes with TR≈3.2 ms, corresponding to five-minute acquisition. In Fig. 2, we compared the image quality of the reconstructions of different approaches based on the pre-contrast data. We also include the high SNR post-contrast reconstructions using the proposed scheme. We observe that the proposed scheme is able to offer higher SNR reconstructions, which are less blurred than competing methods on the pre-contrast data. In Fig. 3, we show the motion-compensated reconstructions of the post-contrast datasets from both the healthy subject and fibrotic subject. In Fig. 4, we show the sample motion fields $$$\Phi_t$$$ for a specific time instance, which is obtained as a by-product. We noticed that the post-contrast fibrotic subject dataset has a shoulder movement during the scan, which is captured by the latent vectors of the proposed scheme as illustrated in Fig. 5, respectively. From the movie shown in Fig. 5, we see that the subject moved the shoulder during the scan.

Conclusion

We introduced an unsupervised motion-compensated manifold reconstruction scheme for free‐breathing pulmonary MRI from highly undersampled measurements. The proposed scheme is observed to offer improved SNR and reduced blurring, compared to competing methods. In addition, the proposed approach is observed to be robust to bulk motion during the scan.

Acknowledgements

This work is supported by NIH under Grants R01EB019961, R01AG067078-01A1 and R01HL126771.