0638
Deep learning-based relative B1+-mapping in the human body at 7T1Physikalisch-Technische Bundesanstalt, Braunschweig and Berlin, Germany, 2Technical University of Munich, Munich, Germany, 3Imperial College London, London, United Kingdom, 4Medical Physics in Radiology, German Cancer Research Center (DKFZ), Heidelberg, Germany, 5Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States
Synopsis
In this work, we estimate relative 2D B1+-maps from initial localizer scans using deep learning at 7T. We investigate 7 UNets and MultiResUNets architectures to estimate complex, channel-wise, relative 2D B1+-maps of 8 transmit channels from a single gradient echo localizer obtained with 32 receive channels. The networks are evaluated in 5 unseen volunteers not included in the training library by comparing the prediction with the acquired relative B1+-maps using different evaluation metrics for homogeneous B1+ phase shimming. Our approach saves additional B1+-mapping scans, and, hence, overcomes long calibration times in the human body at 7T.
Purpose
Ultrahigh magnetic fields (UHF) body MRI is often accompanied by pronounced spatial variations of the transmit (Tx) magnetic field (B1+) leading to a spatially varying flip angle1. To overcome this issue, multi-channel Tx coils in combination with parallel transmission (pTx) techniques1,2 are typically used. While calibration-free pTx approaches exist3, such techniques are usually applied subject-tailored, which requires mapping the spatial B1+-distribution of all Tx channels in the beginning of the study. In the human brain, B1+-maps can be obtained in 40 seconds with 8 Tx channels rendering it feasible for clinical routine4. However, in the human body (relative) B1+-mapping is limited by the larger FOV, respiratory and cardiac motion, and B1+-power leading to long acquisition times5,6,7.The idea here is to overcome such long calibration times for UHF body MRI and derive B1+-maps using deep learning (DL) from initial localizer scans, that are typically acquired for planning. Thus, this approach would spare the B1+-mapping scan. To this end, we investigate 7 UNets and MultiResUNets architectures to estimate channel-wise, relative 2D B1+-maps of 8 Tx channels from a single gradient echo (GRE) localizer obtained with 32 receive (Rx) channels. The neural networks (NNs) are evaluated in 5 unseen volunteers not included in the training library by comparing predictions of the NNs with acquired relative B1+-maps using different evaluation metrics.
Methods
Data was acquired in 29 subjects on a 7T whole body MRI system (Magnetom 7T, Siemens, Erlangen, Germany) with a 32-channel body array coil driven in 8Tx/32Rx-mode using a Cartesian, cardiac GRE sequence ($$$T_{R}=496.32\,\mathrm{ms}$$$, $$$T_{E}=2.87\,\mathrm{ms}$$$, $$$\mathrm{resolution}=4.0\times4.0\times4.0\,\mathrm{mm}^3$$$, $$$\mathrm{FOV}=386\times386\,\mathrm{mm}^2$$$) obtained under breathhold without cardiac triggering. First, a GRE image is obtained with all Tx channels transmitting using a default shim (i.e., the localizer). Then, the acquisition is repeated 8 times where only a single Tx channel is active each. Based on the latter scans, channel-wise, relative 2D B1+-maps are derived8.The 7 investigated NNs are based on a standard UNet9 and MultiResUNet10 (see Figure 1a)-b)) with a mean squared error (MSE), structural similarity measure (SSIM), and perpendicular loss11 as loss functions. All networks were trained on a library containing 88 data sets from 24 volunteers and were validated using 14 data sets from 5 volunteers. The networks use complex-valued GRE localizer (32 Rx channels) as input. The real and imaginary parts of the complex images and the combined localizer magnitude are concatenated to a 96x96x65 matrix. As ground truth (GT), the network is trained on the 8 relative B1+-maps with a size of 96x96x16. The data structure is depicted in Figure 1c). The training parameters are: ADAM optimizer, learning rate $$$\eta =1\cdot10^{-3}$$$, 500 epochs, batch size = 16. DL is performed on a 24 GB NVIDIA Titan RTX on premise. Mismatch between GT and B1+-map prediction is evaluated by the MSE, mean absolute error (MAE), and SSIM as metrics. Homogeneous B1+ phase shimming (minimizing the coefficient-of-variation (CoV)) is subsequently performed on the predicted B1+-maps. Cartesian GRE scans ($$$T_{R}=383.40\,\mathrm{ms}$$$, $$$T_{E}=1.57\,\mathrm{ms}$$$, $$$\mathrm{resolution}=1.5\times1.5\times4.0\,\mathrm{mm}^3$$$, $$$\mathrm{FOV}=384\times288\,\mathrm{mm}^2$$$) were performed before/after shimming to qualitatively validate the shimming results.
Results and Discussion
Figure 2a) shows the mean values of the MSE, MAE and SSIM for all validation data sets of the designed 7 NNs. The network with the highest structural similarity, NN I, is chosen for further evaluation. NN I generates on average B1+-maps with an MSE of $$$3.6\cdot10^{-3}$$$, MAE of $$$0.0228$$$ and SSIM of $$$0.7334$$$ with respect to the GT. When switching from validation to training data (Figure 2b)) a decrease in the MSE to $$$7.9\cdot10^{-4}$$$ and MAE to $$$0.0102$$$, as well as an increase in the SSIM to $$$0.8009$$$ are observed reflecting overfitting. Figure 3 shows estimated, channel-wise and combined B1+-maps for a seen training data set compared to the GT. NN I produces B1+-maps with a relative error for the magnitude of $$$<20\,\%$$$ in the heart and liver. In comparison, Figure 4 shows predicted B1+-maps for a data set not included in the training library. While qualitatively a good agreement with GT data is globally observed, the NN fails to predict the magnitude in localized regions, which are associated with phase wraps.Figure 5 shows DL predicted B1+-maps in the context of static phase-only B1+ shimming as an application. Shimming is very sensitive to alterations of the B1+ phases between prediction and GT. This is reflected by the calculated magnitude images after applying a shim optimized on the GT B1+-maps, that is also applied on the predicted maps (Figure 5b)) and vice versa (Figure 5c)). However, in this case, the prediction is accurate enough to improve the homogeneity over a 2D region of interest in the heart from $$$48\,\%$$$ to $$$27\,\%$$$, which was experimentally confirmed (Figure 5d)).
Conclusion
These promising results indicate the general feasibility to estimate complex channel-wise, 2D relative B1+-maps in the human heart at 7T from a quick single GRE localizer scan. Although we achieved overall a good accuracy, results vary between subjects and the NNs still suffer from overfitting and false signal dropouts associated with phase wraps. These insights serve as a basis for more general approaches like the use of a complex-valued network and extension to a 3D case.Acknowledgements
We gratefully acknowledge funding from the German Research Foundation (GRK2260, BIOQIC).References
1) Ladd ME, Bachert P, Meyerspeer M, Moser E, Nagel AM, Norris DG, Schmitter S, Speck O, Straub S, Zaiss M. Progress in nuclear magnetic resonance spectroscopy Pros and cons of ultrahigh-field MRI/MRS for human application. Prog Nucl Magn Reson Spectrosc. 2018;109:1-50.
2) Padormo F, Beqiri A, Hajnal JV, Malik SJ. Parallel transmission for ultrahigh-field imaging. NMR Biomed. 2016;29:1145-1161.
3) Aigner CS, Dietrich S, Schaeffter T, Schmitter S. Calibration-free pTx for the human heart at 7T via 3D universal pulses. Magn Reson Med. 2021;00:1–15.
4) Herrler J, Liebig P, Gumbrecht R, Ritter D, Schmitter S, Maier A, Schmidt M, Uder M, Doerfler A, Nagel AM. Fast online-customized (FOCUS) parallel transmission pulses: A combination of universal pulses and individual optimization. Magn Reson Med. 2021;85:3140–3153.
5) Dietrich S, Aigner CS, Kolbitsch C, Mayer J, Ludwig J, Schmidt S, Schaeffter T, Schmitter S. 3D Free-breathing multichannel absolute B1+ Mapping in the human body at 7T. Magn Reson Med. 2021;85:2552–2567.
6) Brunheim S, Gratz M, Johst S, Bitz AK, Fiedler TM, Ladd ME, Quick HH, Orzada S. Fast and accurate multi-channel B1+ mapping based on the TIAMO technique for 7T UHF body MRI. Magn Reson Med. 2018;79:2652-2664.
7) Padormo F, Hess AT, Alijabar P, Malik SJ, Jezzard P, Robson MD, Hajnal JV, Koopmans PJ. Large dynamic range relative B1+ mapping. Magn Reson Med. 2016;76:490–499.
8) Van de Moortele PF, Ugurbil K. Very Fast Multi Channel B1 Calibration at High Field in the Small Flip Angle Regime. Proc. ISMRM 2009; 367.
9) Ronneberger O, Fischer P, Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation. MICCAI. 2015;9351:234-241.
10) Ibtehaz N, Rahman MS. MultiResUNet: Rethinking the U-Net architecture for multimodal biomedical image segmentation. Neural Networks. 2020;121:74-87.
11) Terpstra M, Maspero M, Lagendijk J, van den Berg CAT. Rethinking complex image reconstruction: ⟂-loss for improved complex image reconstruction with deep learning. Proc. ISMRM 2021; 1751.
Figures
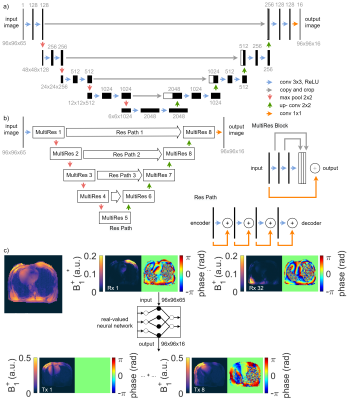
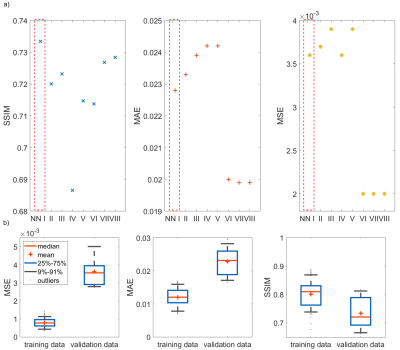
Figure 2: a) Networks evaluated for the mean of the mean squared error (MSE), mean absolute error (MAE), and structural similarity measure (SSIM) for unseen data. The data for NN I – NN V is relative to channel Tx1, for NN VI – NN VIII it has no reference. NN I – III are UNets with a perpendicular loss, MSE, and SSIM. NN IV – NN VIII are MultiResUNets with a MSE (IV/VI), perpendicular loss (V/VII), and SSIM (VIII). b) Comparing seen and unseen data for NN I. The MSE and MAE for seen data is one order of magnitude lower than for unseen. The SSIM for training data is above 0.80 compared to 0.74 for validation.
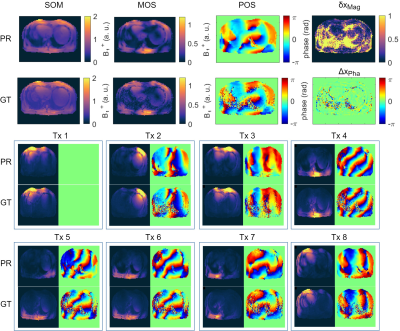
Figure 3: Prediction (PR) compared to the ground truth (GT) for a seen training data set. The PR of the sum of magnitudes (SOM), magnitude of sum (MOS) and phase of sum (POS) over all 8 transmission channels are in good agreement with the GT. All signal dropouts in the MOS and phase wraps in the POS are estimated accordingly. This leads to a relative error δxMag of the magnitude in the heart and liver of <20% and no visible structure in the absolute error ΔxPha for the phase. In the bottom, channel-wise comparison of the B1+-maps of PR and GT. Only small deviations for the seen data are visible.
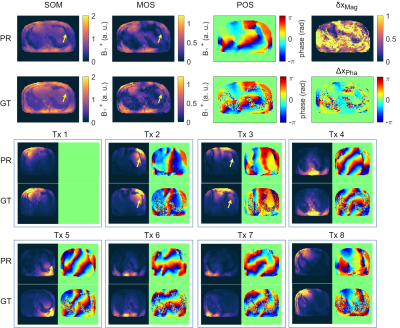
Figure 4: Prediction (PR) compared to the ground truth (GT) for an unseen data set. The PR of the sum of magnitudes (SOM), magnitude of sum (MOS) and phase of sum (POS) over all 8 transmission channels are in good agreement to the GT. False signal dropouts (yellow arrows) associated to phase wraps are visible. This leads to larger relative δxMag and absolute errors ΔxPha in magnitude and phase. In the bottom, channel-wise comparison of the B1+-maps of PR and GT. In Tx1, Tx4, Tx6, Tx7 and Tx8 only small deviations are visible. In Tx2, Tx3, Tx5 signal dropouts associated with phase wraps can be seen.
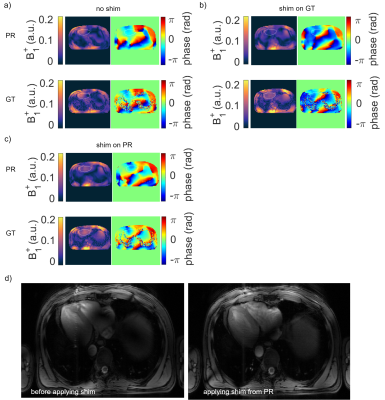
Figure 5: Predicted (PR) and ground truth (GT) B1+-maps (MOS) for different shims. a) The default setting leads to signal cancellations in the heart. b) A homogenous shim optimized on the GT applied to the PR and GT. An improved homogeneity leads to a reduced coefficient of variation from 49% to 9% for the GT and 48% to 27% for the PR. c) shows the results vice versa. The homogeneity improves for the GT from 49% to 16% and for the PR from 48% to 13%. d) In-vivo localizer scans without and with a homogenous shim calculated on the PR of the network. This is reflected by an improved homogeneity in the heart.