Introduction

Deuterium metabolic imaging (DMI)¹ is an emerging technique that can spatially map metabolism in vivo through the intake of deuterium-labeled substrates such as [6,6′-²H₂]-glucose. At ultra-high fields (≥7T), deuterium MRSI (DMRSI) benefits from a significantly increased signal-to-noise ratio (SNR) and improved spectral resolution². However, achieving full coverage of the human liver with high spatial resolution within a short acquisition time is challenging. The subspace imaging framework SPICE^3,4 was proposed to enable fast acquisition of 3D MRSI with high resolution. The subspace-based image reconstruction⁵ was shown to reduce spectral noise in 3D ³¹P MRSI of the human brain. In this work, we demonstrate the application of low-rank and subspace model reconstruction (LRSM) for effective denoising of 3D DMRSI data from the human liver at 7T.

Methods

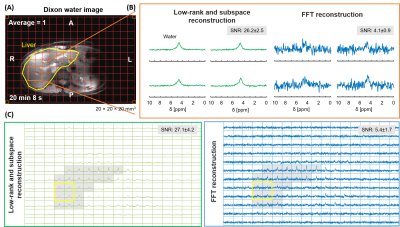
1. Experiments
Two healthy volunteers were scanned at a 7T MR system (Achieva, Philips, Netherlands) using a transmit-receive body array, including 4 proton dipole antennas and 4 deuterium loop coils. For one volunteer, a 3D DMRSI scan was obtained 2.5 hours after oral intake of deuterated glucose.

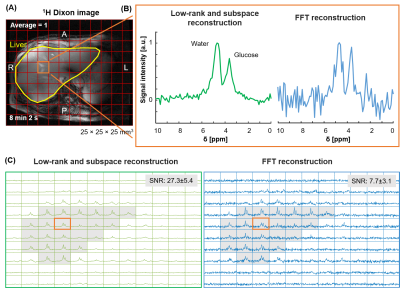
Scan parameters: DMRSI in the human liver at natural abundance: 20×20×20mm³ voxels, FOV=240(AP)×360(RL)×300(FH)mm³, TR/TE=371/1.0ms, 1ms block pulse, spectral bandwidth=1443Hz, average=1, and acquisition time=20min 8s. DMRSI after oral glucose intake: 25×25×25mm³ voxels, FOV=250(AP)×300(RL)×300(FH)mm³, TR/TE=333/1.95ms, spectral bandwidth=5000Hz, weighted averages=4, acquisition time=10min 35s.

2. Numerical simulation
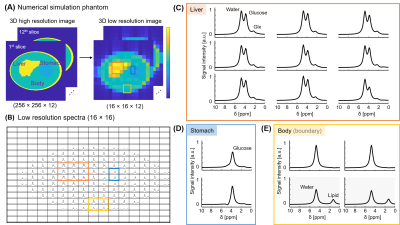
A 3D high-resolution image (matrix size=256x256x12) was generated with three distinct compartments for numerical simulation: liver, stomach, and the rest of the body (including a subcutaneous fat layer). Metabolite signals for water, glucose, Glx, and lipids were generated by varying the amplitude of each signal using a Lorentzian lineshape. Deuterium spectra were simulated with a 10kHz spectral bandwidth and 2048 points. The high-resolution was down-sampled to the resolution of a typical DMI acquisition. Complex Gaussian noise (i.e., N(0, 1)) was added to the simulated deuterium signals with increasing noise standard deviation (0.01-0.2).

3. Image Reconstruction
The subspace model^3,4,5,6 exploits spatiotemporal correlation⁷ of the MRSI signals:

$$$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\mathrm{\hat{\rho}(\mathbf{r},t)} = \sum_{l=1}^{L} \mathit{u}_l(\mathbf{r})\mathit{v}_l(t), $$$

where $$$\big\{\mathit{u}_l(\mathbf{r})_{l=1}^L \big\}, \, \big\{\mathit{v}_l(t)_{l=1}^L \big\}$$$ denote a set of spatial and temporal basis functions, respectively, and the model order $$$L$$$. Our approach employs a low-rank and subspace modeling where a temporal subspace is estimated from the fully sampled 5×5×5 k-space center region. Specifically, the unknown spatial basis $$$\mathbf{U}$$$ is estimated by solving the following least-squares problem:

$$$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\hat{\mathrm{U}} = \underset{\mathrm{U}}{\text{argmin}} \, \|\mathbf{d} - \Omega (\mathbf{F} \mathbf{U} \hat{\mathbf{V}} ) \|_{\ell_2}^2, \\$$$

where $$$ \mathbf{d} \in \mathbb{C}^{P \times 1}$$$ denotes the vector of k-space data, $$$\Omega(\cdot) : \mathbb{C}^{N \times M} \rightarrow \mathbb{C}^{P \times 1}$$$ is a linear operator that concatenates the measured data into a vector, $$$\mathbf{F} \in \mathbb{C}^{N \times N}$$$ is the Fourier encoding matrix, and the columns of $$$\mathbf{U} \in \mathbb{C}^{N \times L}$$$ and rows of $$$\hat{\mathbf{V}} \in \mathbb{C}^{L \times M}$$$ span the spatial and temporal subspaces of the Casorati matrix. The Roemer equal noise algorithm⁸ was used for channel combination. Data processing were developed in-house using MATLAB (The MathWorks, Inc, Natick, MA).

4. Analysis
After 0^th and 1^st order phase correction, the SNR was calculated according to $$$\mathit{SNR}=\mathit{I}_{\mathit{water}}/\mathit{\sigma}(\mathit{I}_{\mathit{noise}})$$$, where $$$\mathit{I}_{\mathit{water}}$$$ is the water signal intensity and $$$\mathit{\sigma}(\mathit{I}_{\mathit{noise}})$$$ the standard deviation of the noise (8-12 ppm). Glucose and water maps were calculated by fitting the signal using the AMARES algorithm⁹.

Results and Discussion

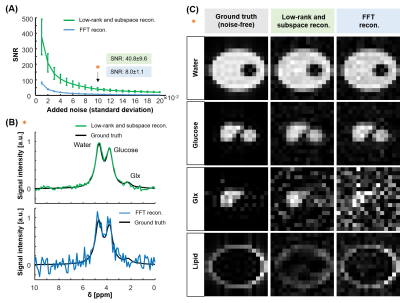
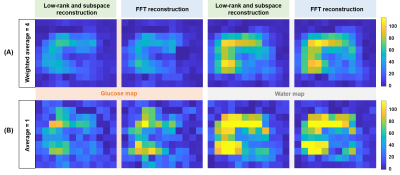
Figure 1 shows the generated numerical phantom mask in high-resolution and after down-sampling to low-resolution (Fig. 1A). The SNR (Fig. 2A) was calculated for different additive noise after applying two reconstruction methods: LRSM and FFT reconstruction. The LRSM reconstruction increased the SNR approximately 5-fold at noise level 10 (i.e., a noise standard deviation of 0.1). The metabolite maps of water and glucose (Fig. 2C) are similar to the ground truth when using either FFT or LRSM reconstruction with noise level 10. The Glx maps were noisier than the ground truth, especially for the FFT reconstruction (Fig. 2C). The average SNR (Fig. 3C) in the ROI of the liver (natural abundance DMRSI) was approximately 5-fold higher for LRSM compared to FFT reconstruction. While the natural abundance deuterated water signal was barely visible in some voxels with FFT reconstruction, LRSM reconstruction clearly showed signals in the liver. Figure 4 shows DMI data in the liver after oral intake of deuterated glucose for both reconstructions. The noise (Fig. 4B) is high and could be misinterpreted as a Glx signal for the FFT reconstruction, which is not the case for the LRSM reconstruction. The average SNR (Fig. 4C) of the deuterated water signal in the liver was about 3.5 times higher for the LRSM reconstruction. Glucose and water metabolite maps were created for both reconstruction methods (Fig. 5). The glucose map generated from the data with a single average showed more noise for the FFT reconstruction than for the LRSM reconstruction.

Conclusion

This work demonstrates the implementation of low-rank and subspace modeling reconstruction of 3D DMI data of the human body at 7T. The reconstruction method reduces the noise level in the spectra, enabling metabolite detection in low SNR data. The enhanced metabolite detection could potentially increase spatial resolution and/or decrease acquisition time of 3D DMRSI, for example in combination with fast acquisition techniques such as DEPSI¹⁰.

Acknowledgements

This project has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement (No. 813120) and was funded by an HTSM grant from NWO TTW (project number 17134) and by a FET Innovation Launchpad grant from the EU (grant number 850488).