0627
Addressing Concomitant Gradient Phase Errors in Chemical Shift-Encoded MRI with a Pass-Specific Phase Fitting Method
Nathan Tibbitts Roberts, BS1,2, Diego Hernando, PhD1,2,3,4, Nikolaos Panagiotopoulos, MD1, and Scott B Reeder, MD, PhD1,3,4,5,6
1Radiology, University of Wisconsin - Madison, Madison, WI, United States, 2Electrical and Computer Engineering, University of Wisconsin - Madison, Madison, WI, United States, 3Medical Physics, University of Wisconsin - Madison, Madison, WI, United States, 4Biomedical Engineering, University of Wisconsin - Madison, Madison, WI, United States, 5Medicine, University of Wisconsin - Madison, Madison, WI, United States, 6Emergency Medicine, University of Wisconsin - Madison, Madison, WI, United States
1Radiology, University of Wisconsin - Madison, Madison, WI, United States, 2Electrical and Computer Engineering, University of Wisconsin - Madison, Madison, WI, United States, 3Medical Physics, University of Wisconsin - Madison, Madison, WI, United States, 4Biomedical Engineering, University of Wisconsin - Madison, Madison, WI, United States, 5Medicine, University of Wisconsin - Madison, Madison, WI, United States, 6Emergency Medicine, University of Wisconsin - Madison, Madison, WI, United States
Synopsis
This work presents a complex-based fitting method to address concomitant gradient (CG) phase errors for time-interleaved (i.e., multi-pass) chemical shift-encoded (CSE) MRI estimation of proton density fat fraction (PDFF) and R2* through a joint estimation of pass-specific phase terms. The proposed method does not require prior knowledge of gradient waveforms. The proposed fitting method removed significant PDFF and R2* estimation errors in both phantom and in vivo evaluations away from isocenter. An evaluation in 29 clinical liver datasets demonstrated reduced PDFF bias and variability (8.4% improvement in the coefficient of variation), even when the imaging volume was centered at isocenter.
Introduction
Multi-echo chemical shift-encoded (CSE)-MRI is an established method for measuring proton density fat fraction (PDFF) and R2* as biomarkers of tissue fat and iron content, respectively1–4. At 3.0T, CSE-MRI is routinely acquired in two or more time-interleaved passes (i.e., multi-pass). Multi-pass acquisitions permit high spatial resolution while maintaining optimal echo spacing5–7; however, they also exacerbate concomitant gradient (CG) phase errors8,9. Away from isocenter, CG phase errors cause spatially-varying bias when estimating B0 off-resonance, R2*, and PDFF7,8.While methods have been proposed to correct CSE-MRI multi-pass acquisitions for CG phase errors6–8, they generally require knowledge of the gradient waveforms. In this work, we present a fitting method that addresses concomitant gradient phase errors in PDFF and R2* estimation without prior knowledge of gradient waveforms.
Theory
CGs are magnetic field variations induced as the by-product of the imaging gradients9. For a position relative to isocenter (x=0, y=0, z=0), CGs are approximated by: \begin{equation}\begin{aligned}B_{CG}(x,y,z,t)&=\frac{1}{2B_0}[G_x^2(t)z^2+G_y^2(t)z^2+G_z^2(t)\frac{x^2+y^2}{4}\\&-G_x(t)G_z(t)xz-G_y(t)G_z(t)yz]\end{aligned}\tag{1}\end{equation}where $$$G_x(t)$$$, $$$G_y(t)$$$, and $$$G_z(t)$$$ are the imaging gradients8,9.We begin with the following phase-constrained CSE-MRI spoiled gradient echo (SGRE) signal model10,11:\begin{equation}s_n(\eta,R_2^*,\psi,M_0,\phi)=M_0e^{i\phi}(1-\eta+\eta\,C_F(t_n))e^{-R_2^*t_n}e^{i2\pi\psi{}t_n}\tag{2}\end{equation}for N echoes acquired at TEs $$$t_1,t_2,...,t_N$$$. $$$M_0e^{i\phi}$$$ is the complex signal amplitude ($$$M_0$$$) and constant phase ($$$\phi$$$), $$$\eta$$$ is PDFF, $$$\psi$$$ is the B0 field map (Hz), and $$$C_F$$$ is the sum of complex exponentials reflecting a multi-peak spectral model of fat, typically 6 peaks12.
CG phase errors can then be included as:\begin{equation}\begin{aligned}s_{n,CG}(x,y,z,\pmb{\theta})=s_n(\pmb{\theta})e^{-i\phi_{CG}(x,y,z,t_n)}\end{aligned}\tag{3}\end{equation}for $$$\pmb{\theta}=\{\eta,R_2^*,\psi,M_0,\phi\},~$$$where$$$~\phi_{CG}(x,y,z,TE)$$$ is the spatially-dependent phase error attributed to CGs given by\begin{equation}\begin{aligned}\phi_{CG}(x,y,z,TE)=\gamma\int_{0}^{TE}B_{CG}(x,y,z,\tau)\,d\tau\end{aligned}\tag{4}\end{equation}and $$$\gamma$$$ is the gyromagnetic ratio.
Multi-pass acquisitions introduce a delay between echo trains of different passes (Figure 1). Off-isocenter, this results in a constant phase offset between interleaved echo trains and a non-linear phase error across sequential echoes that confounds estimation of PDFF and R2*. As a solution for CG phase error correction without requiring knowledge of the imaging gradients, we propose the following SGRE signal model:\begin{equation}s_{n,p}(\eta,R_2^*,\psi,M_0,\phi_1,…,\phi_P)=M_0e^{i\phi_p}(1-\eta+\eta\,C_F(t_n))e^{-R_2^*t_n}e^{i2\pi\psi^*{}t_n}\tag{5}\end{equation}where $$$\phi_p$$$ is a new pass-specific phase intercept (constant phase term) for the pth pass. As shown in Figure 1, this solution recognizes that passes accrue CG-induced phase errors in parallel: at the same rate but separated by a constant phase offset. We propose to estimate that constant phase offset on a voxel-by-voxel basis. As in single-pass acquisitions, CGs will still bias the estimated B0 off-resonance (now denoted $$$\psi^*$$$).
Methods
Fitting AlgorithmsAll fittings were solved by nonlinear least-squares13, as follows, after initialization with a graph cut algorithm14.
Complex Fitting - Conventional:\begin{equation}\pmb{\widehat{\theta}}=\text{arg}\min\limits_{\pmb{\theta}}\,[\sum_{n=1}^{N}|s_n(\pmb{\theta})-s_{n,meas}|^2],\qquad\,for\,\pmb{\theta}=\{\eta,R_2^*,\psi,M_0,\phi\}\tag{6}\end{equation}
Complex Fitting - Proposed:\begin{equation}\pmb{\widehat{\theta}}=\text{arg}\min\limits_{\pmb{\theta}}\,[\sum_{p=1}^{P}\sum_{n\in{N_p}}^{}|s_{n,p}(\pmb{\theta})-s_{n,p,meas}|^2],\qquad\,for\,\pmb{\theta}=\{\eta,R_2^*,\psi,M_0,\phi_1,...,\phi_P\}\tag{7}\end{equation}
where $$$N_p$$$ denotes the set of echo indices acquired in the pth pass.
Magnitude Fitting - Reference:\begin{equation}\pmb{\widehat{\theta}}=\text{arg}\min\limits_{\pmb{\theta}}\,[\sum_{n=1}^{N}(|s_n(\pmb{\theta})|-|s_{n,meas}|)^2],\qquad\,for\,\pmb{\theta}=\{\eta,R_2^*,M_0\}\tag{8}\end{equation}
Cramér-Rao Lower Bound Analysis
Cramér-Rao Lower Bound (CRLB) analysis15 was used to predict and compare the noise performance of the proposed (Eq. [5]), conventional (Eq. [2]), and magnitude (magnitude of Eq. [2]) fittings.
Phantom Acquisitions
Multi-pass phantom acquisitions were performed on a 3.0T clinical MRI system (Discovery MR750, GE Healthcare, Waukesha, WI) with a 32-channel phased-array torso coil (NeoCoil, Pewaukee, WI). Estimates from the conventional (with and without CG correction), magnitude, and proposed fitting methods were compared.
In-Vivo Acquisitions
Data were acquired at and 12cm off isocenter in the liver of a healthy volunteer. PDFF estimates from the conventional, magnitude, and proposed fittings were compared.
Data from 29 clinical patients, acquired in a previous study16, were reprocessed. Acquisitions were performed using a clinical protocol with the imaging volume positioned at isocenter. Regions-of-interest (ROI) were placed in each Couinaud segment of the liver17 and Bland-Altman analysis was used to evaluate the proposed fitting.
Results
Cramér-Rao Lower Bound AnalysisFigure 2 shows the CRLB results. Compared to magnitude fitting, the proposed fitting method demonstrates improved noise performance within the range of common echo time combinations.
Phantom Acquisitions
Figure 3 shows PDFF and R2* estimated along a profile in the z-direction through the middle of the water phantom. The proposed fitting method removed PDFF and R2* estimation errors up to 12% and 10s-1, respectively, at ±12cm off isocenter.
In-Vivo Acquisitions
Figure 4 shows the proposed method reduced PDFF bias by ~10% in the liver 12cm off isocenter. Using magnitude fitting as a reference, analysis of the 29 clinical liver datasets showed the proposed fitting reduced absolute PDFF bias by 0.6% on average and reduce the coefficient of variation from 16% to 7.6% compared to the conventional fitting (Figure 5).
Discussion
We have presented a novel fitting method that provides PDFF and R2* measurements corrected for CG-induced phase errors in multi-pass acquisitions with uniformly spaced echoes. This is particularly relevant at 3.0T where multi-pass acquisitions are routinely used to achieve high spatial resolution while maintaining optimal echo spacing for water-fat separation.CG-induced phase errors in multi-pass CSE-MRI acquisitions can result in significant estimation biases that increase quadratically away from isocenter. The severity is particularly notable for PDFF, with clinically relevant bias across the liver, even when the imaging volume is centered at isocenter. The proposed fitting enables PDFF and R2* quantification corrected for CG phase errors without prior knowledge of imaging gradient waveforms, reducing both bias and apparent variability in PDFF and R2* estimates between different locations across the liver.
Acknowledgements
This work was supported by the NIH (K24 DK102595, R01 DK083380, R01 DK088925, R01 DK100651, R01 DK117354, R41 EB025729, T32CA009206, UL1TR00427). The authors also acknowledge GE Healthcare who provides research support to the University of Wisconsin-Madison. Finally, Dr. Reeder is a Romnes Faculty Fellow, and has received an award provided by the University of Wisconsin-Madison Office of the Vice Chancellor for Research and Graduate Education with funding from the Wisconsin Alumni Research Foundation.References
1. Caussy C, Reeder SB, Sirlin CB, Loomba R. Noninvasive, Quantitative Assessment of Liver Fat by MRI-PDFF as an Endpoint in NASH Trials. Hepatol. Baltim. Md 2018;68:763–772 doi: 10.1002/hep.29797.2. Hernando D, Levin YS, Sirlin CB, Reeder SB. Quantification of liver iron with MRI: state of the art and remaining challenges. J Magn Reson Imaging 2014;40:1003–21 doi: 10.1002/jmri.24584.
3. Wood JC, Enriquez C, Ghugre N, et al. MRI R2 and R2* mapping accurately estimates hepatic iron concentration in transfusion-dependent thalassemia and sickle cell disease patients. Blood 2005;106:1460–1465 doi: 10.1182/blood-2004-10-3982.
4. Hernando D, Cook RJ, Qazi N, Longhurst CA, Diamond CA, Reeder SB. Complex confounder-corrected R2* mapping for liver iron quantification with MRI. Eur. Radiol. 2020 doi: 10.1007/s00330-020-07123-x.
5. Hernando D, Hines CD, Yu H, Reeder SB. Addressing phase errors in fat-water imaging using a mixed magnitude/complex fitting method. Magn Reson Med 2012;67:638–44 doi: 10.1002/mrm.23044.
6. Ruschke S, Eggers H, Kooijman H, et al. Addressing phase errors in quantitative water-fat imagin at 3T using a time-interleaved multi-echo gradient-echo acquisition. In: Proceedings of the 23rd Annual Meeting of ISMRM. Toronto, Ontario, Canada; p. 3657.
7. Ruschke S, Eggers H, Kooijman H, et al. Correction of phase errors in quantitative water–fat imaging using a monopolar time-interleaved multi-echo gradient echo sequence. Magn. Reson. Med. 2017;78:984–996 doi: https://doi.org/10.1002/mrm.26485.
8. Colgan TJ, Hernando D, Sharma SD, Reeder SB. The effects of concomitant gradients on chemical shift encoded MRI. Magn. Reson. Med. 2017;78:730–738 doi: https://doi.org/10.1002/mrm.26461.
9. Bernstein MA, Zhou XJ, Polzin JA, et al. Concomitant gradient terms in phase contrast MR: Analysis and correction. Magn. Reson. Med. 1998;39:300–308 doi: https://doi.org/10.1002/mrm.1910390218.
10. Bydder M, Yokoo T, Yu H, Carl M, Reeder SB, Sirlin CB. Constraining the initial phase in water–fat separation. Magn. Reson. Imaging 2011;29:216–221 doi: https://doi.org/10.1016/j.mri.2010.08.011.
11. Horng DE, Hernando D, Reeder SB. Quantification of Liver Fat in the Presence of Iron Overload. J Magn Reson Imaging 2017;45:428–39 doi: 10.1002/jmri.25382.
12. Yu H, Shimakawa A, McKenzie CA, Brodsky E, Brittain JH, Reeder SB. Multiecho water-fat separation and simultaneous R2* estimation with multifrequency fat spectrum modeling. Magn Reson Med 2008;60:1122–34 doi: 10.1002/mrm.21737.
13. Galassi M, Davies J, Theiler J, et al. GNU Scientific Library Reference Manual (3rd Ed.).
14. Hernando D, Kellman P, Haldar JP, Liang Z-P. Robust water/fat separation in the presence of large field inhomogeneities using a graph cut algorithm. Magn. Reson. Med. 2010;63:79–90 doi: https://doi.org/10.1002/mrm.22177.
15. Scharf LL, Mcwhorter LT. Geometry of the Cramer-Rao Bound. Signal Process. 1993;31:301–311 doi: Doi 10.1016/0165-1684(93)90088-R.
16. Hernando D, Zhao R, Taviani V, et al. Repeatability and reproducibility of confounder-corrected R2* as a biomarker of liver iron concentration: interim results from a multi-center, multi-vendor study at 1.5T and 3T. In: Montreal, Canada; 2019.
17. Campo CA, Hernando D, Schubert T, Bookwalter CA, Pay AJV, Reeder SB. Standardized Approach for ROI-Based Measurements of Proton Density Fat Fraction and R2* in the Liver. Am. J. Roentgenol. 2017;209:592–603 doi: 10.2214/AJR.17.17812.
Figures
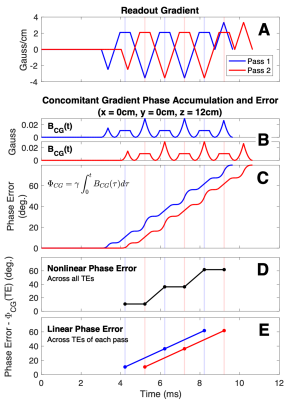
Figure 1. Concomitant gradient phase errors in multi-pass acquisitions (A) cause spatially dependent non-linear phase accumulation (B, C, D) across sequential echo times (TEs) that lead to errors in PDFF and R2* estimation. However, these phase errors are linear across sequential TEs in the same pass and parallel between passes (E). The proposed fitting method accounts for the difference between CG-induced phase errors of different passes by including pass-specific phase terms in the CSE-MRI signal model. Shown are phase errors attributed to CGs 12cm (superior, +z) from isocenter.
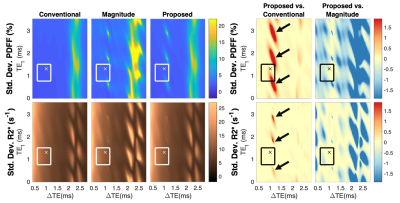
Figure 2. Noise performance of the proposed fitting method is similar to conventional fitting and improved from magnitude fitting. The standard deviations of estimated PDFF and R2* are plotted as a function of echo times. The black arrows indicate regions of noise amplification; however, these regions would yield biased estimates in the conventional fitting. Typical choices for echo times are shown by the boxes, with X denoting echo times used in this work. Data were calculated for 6 echoes at 3.0T with PDFF=10%, R2*=45s-1, ψ*=0Hz, M0=100, ϕ1=0, and ϕ2=π/15, for SNR=M0/σ=30.
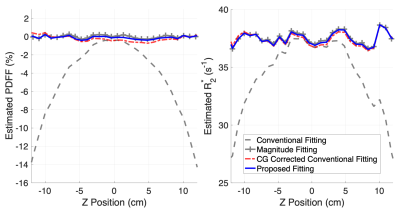
Figure 3. The proposed reconstruction removes significant errors in PDFF and R2* estimation caused by CG-induced phase errors. Estimation with the proposed fitting (solid blue) is similar the conventional fitting after CG correction (dashed red) and magnitude fitting (marked gray). Estimates are shown for a line through the center of a homogeneous NiCl2- and NaCl-doped water phantom with 0% PDFF and homogeneous R2*. Data were acquired with the following imaging parameters: 6 echoes, TE1=1.3ms, ΔTE=1.0ms, TR=10.6ms, flip angle=3o, FOV=21×21×48cm3, and averaged 12 times.
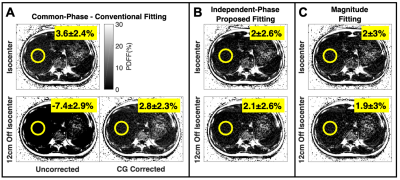
Figure 4. The proposed fitting (B) can avoid significant PDFF estimation errors (A, off isocenter, uncorrected) caused by concomitant gradients in multi-pass acquisitions. Measurements shown are the mean and standard deviation of PDFF estimates within the ROI. Acquisition parameters included: single breath hold, 6 echoes (2 passes, 3 echoes/pass, monopolar), TE1=1.3ms, ΔTE=1.0ms, flip angle=3o, TR=7.4ms, FOV=35×35×48cm3, 192×160×48 matrix, and parallel imaging acceleration factors of 2 (phase) and 1.5 (slice).
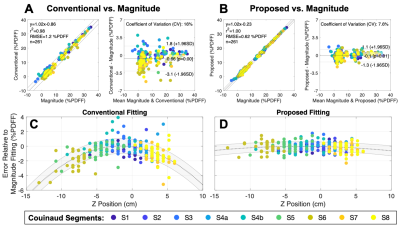
Figure 5. The proposed fitting reduces clinically relevant PDFF bias and variability across the liver. Markers represent average error relative to magnitude fitting for an ROI, with color indicating Couinaud segment (n=261: 29 patients, 9 segments/patient). In addition to Bland-Altman analysis (A, B), error is shown as a function of position for both fittings along with a quadratic regression (C, D). Parameters: 6 echoes (3 echoes/pass, monopolar), TE1=1.2ms, ΔTE=1.0ms, TR=8.02ms, flip angle=3o, FOV=40×32×25.6cm3, 256×144×32 matrix, corner-cutting, and parallel imaging.
DOI: https://doi.org/10.58530/2022/0627