0625

Increasing the T2 sensitivity of MR-STAT sequences by small quadratic RF phase increments

Hongyan Liu¹, Tom Bruijnen¹, Maaike van Haandel¹, Oscar van den Heide¹, Miha Fuderer¹, Cornelis A.T. van den Berg¹, and Alessandro A.T. Sbrizzi¹
¹Computational Imaging Group for MR diagnostics & therapy, Center for Image Sciences, UMC Utrecht, Utrecht, Netherlands

Synopsis

We propose a new method to increase the T2 encoding ability of MR-STAT sequences, according to a recently developed strategy for T2 mapping. Recent work has shown that RF phase modulated GRE sequences with small quadratic phase increments can effectively encode T2 information into the phase of the signal. In this abstract, we show that by incorporating a simple and similar RF modulation strategy in 2D MR-STAT sequences, T2 sensitivity of transient-state gradient-spoiled sequences is improved, and therefore T2 maps as well as the proton density maps (PD) can be reconstructed with higher accuracy.

Introduction

Transient-state GRE (gradient-echo) sequences with gradient-spoiling have been used for multi-parametric quantitative imaging in recent years, such as MR-STAT¹ and MR Fingerprinting (MRF)². GRE sequences with short TRs and initial inversion pulse typically have higher T1 encoding compared to T2 encoding, therefore the quantitative imaging techniques using such sequences typically show T2 mapping results with lower SNR. One possible way to reduce this problem is to apply T2 preparation pulses at the start of GRE sequences³.
In this work, we propose a new method to increase the T2 encoding ability of the transient-state, gradient-spoiled GRE sequences according to a recently developed strategy for T2 mapping. Wang et al⁴ showed that RF phase modulated GRE sequences with small quadratic phase increments can effectively encode T2 information into phase maps of the signals while being relatively uncorrelated with T1, so T2-only quantification can be computed from the difference between phase maps acquired from quadratically increasing and decreasing RF phase sequences. In this abstract, we show that a similar RF modulation strategy can be naturally incorporated in the MR-STAT framework. As a consequence, T2 sensitivity of transient-state gradient-spoiled sequences is considerably improved, especially for smaller T2 values (<100ms), and therefore T2 maps as well as the proton density (PD) maps can be reconstructed with higher quality while T1 maps are unaffected. Incorporating RF phase modulation allows us to design transient-state sequences with additional freedom for improving T1, T2 and PD quantification mapping.

Methods

Sequence design

Two different gradient-spoiled 2D MR-STAT sequences are used either with or without RF phase modulation. The two sequences (duration: 8.8 seconds) are used for numerical brain simulations, gel phantom scan and in-vivo brain scan, in order to obtain T1, T2 and PD maps simultaneously. The flip-angle train is shown in Fig.1(a), with a maximum of 81.25 degrees. Similarly as in the reference⁴ , we design a quadratic RF modulation (Fig.1(a)) using the following:
$$$\phi(n)=\begin{cases}0\text{ degree},&n=0,448,\\\phi(n-1)+2n\text{ degree},&0<n<448,\\\phi(n-1)-2n\text{ degree},&448<n<1120.\end{cases}$$$
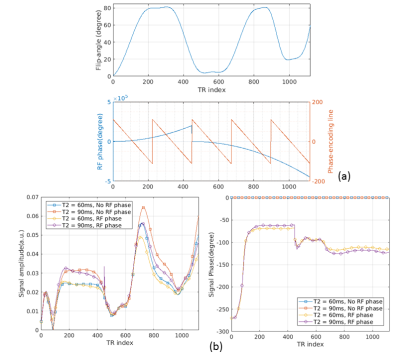
The Cartesian phase-encoding pattern is also shown in Fig.1(a). Five k-spaces are sampled. RF phases are quadratically increasing in the first two k-spaces and then quadratically decreasing in the last three k-spaces.
Fig.1(b) shows the amplitude and phase of the transient-state signals using both MR-STAT sequences for two different sets of parameter values: T1=1000ms, T2=60/90ms. When using the RF phase modulated sequence, a small time-varying phase difference for two signals with different T2 values can be observed, while using the no RF phase sequence, the phases are constantly zero.

Numerical experiment

We simulate numerical data on a digital brain phantom⁵ using both MR-STAT sequences, with and without the small quadratic RF phase increments. Complex Gaussian noise are added to the simulated data with an SNR=20. MR-STAT reconstructions are applied in which T1, T2 and PD maps are computed iteratively, such that the computed volumetric EPG model-based signal matches the simulated signal. For RF phase modulated sequence, MR-STAT framework simply includes the phase modulation in the forward signal model in addition to the flip-angle amplitude modulation.

Gel phantom and in-vivo experiment

Both gel tube phantoms (Eurospin) and in-vivo brain (healthy volunteer) were scanned using the two sequences on a 3T clinical MR system (Ingenia, Philips, Best, The Netherlands) with 13-channel head-coil. Data were first compressed to one single virtual-channel data by singular value decomposition for MR-STAT reconstructions.

Results

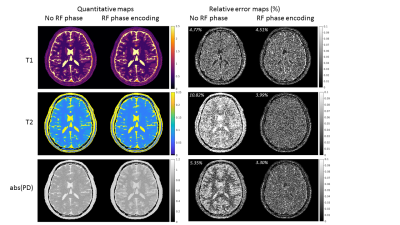
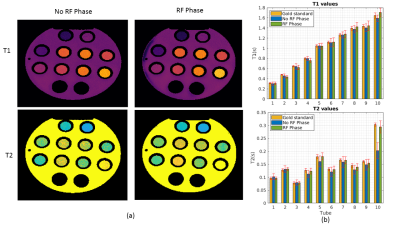
Fig.2 shows the quantitative maps reconstructed from simulation datasets using no RF phase modulation sequence and RF phase modulated sequence with MR-STAT reconstructions. We observe that data using RF phase encoding result in ~50% lower errors in T2 and PD maps. The RF phase increment also eliminates the cross-talk effects between T2 and PD, because only T2 variations affect the phase of the transient signal (Fig.1(b)).
Fig.3(a) shows the T1 and T2 maps reconstructed from gel-phantom data, and Fig.3(b) summarizes the T1 and T2 mean values as well as standard deviations. It can be observed for the standard deviations are approximately 50% lower for tubes with relatively low T2 values (tube 1 to 3) when using RF modulated sequence.
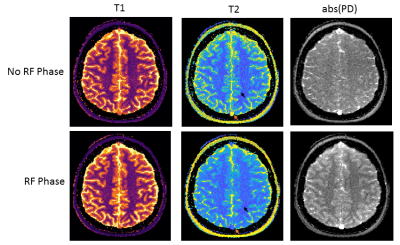
Fig.4 shows the quantitative maps reconstructed from in-vivo data. T2 and PD maps from RF phase modulated sequence show improved contrast-to-noise. Lower CSF values and no hyper-intense blood vessel (in-flow effects) are also observed in T2 maps using the RF modulated sequence.

Discussion and Conclusion

In this work, we provide preliminary evidence with simulations and experiments that small quadratic RF phase modulation can be naturally incorporated in transient-state gradient-spoiled MR sequences. This provides improved T2 encoding capacity, while non-negatively effecting the T1 quantification. Note that the application is fundamentally different than the quadratic RF phase schemes used in bSSFP MRF to increase the sensitivity to T2* ⁶.
We believe that the T2 improvement using RF phase encoding generalizes to other transient-state sequences, such as MR Fingerprinting and therefore warrant further investigation and optimization by the quantitative MRI community. Currently Cramer-Rao-based optimizations are used for sequence design in quantitative imaging such as MR-STAT and MRF^7,8. However, these optimizations currently only take into account RF pulse amplitudes of the flip-angle train. The results here suggest that including the RF phases in the optimization framework may lead to better optimized sequences in the future.

Acknowledgements

No acknowledgement found.

References

[1] van der Heide, Oscar, et al. “Extension of MR-STAT to non-Cartesian and gradient-spoiled sequences.” Proc. Intl. Soc. Mag. Reson. Med. 28 (2020), 0886.

[2] Jiang, Yun, et al. "MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout." Magnetic resonance in medicine 74.6 (2015): 1621-1631.

[3] Hamilton, Jesse I., et al. "MR fingerprinting for rapid quantification of myocardial T1, T2, and proton spin density." Magnetic resonance in medicine 77.4 (2017): 1446-1458.

[4] Wang, Xiaoke, Diego Hernando, and Scott B. Reeder. "Phase‐based T2 mapping with gradient echo imaging." Magnetic resonance in medicine 84.2 (2020): 609-619.

[5] Aubert-Broche, Berengere, Alan C. Evans, and Louis Collins. "A new improved version of the realistic digital brain phantom." NeuroImage 32.1 (2006): 138-145.

[6] Wang, Charlie Yi, et al. "Magnetic resonance fingerprinting with quadratic RF phase for measurement of T2* simultaneously with δf, T1, and T2." Magnetic resonance in medicine 81.3 (2019): 1849-1862.

[7] Fuderer, Miha, et al. “ BLAKJac - A computationally efficient noise-propagation performance metric for the analysis and optimization of MR-STAT sequences.” Proc. Intl. Soc. Mag. Reson. Med. 28 (2020), 3059.

[8] Zhao, Bo, et al. "Optimal experiment design for magnetic resonance fingerprinting: Cramer-Rao bound meets spin dynamics." IEEE transactions on medical imaging 38.3 (2018): 844-861.

Figures

Fig1.(a) The flip-angle train, RF phase modulation and phase-encoding pattern used for simulations and experiments. (b) The amplitude and phase of the transient-state signals using either RF phase modulated MR-STAT sequence or no RF phase sequence for two different T2 values. T1=1000ms for all simulations. Other sequence parameters are: TE=4.0ms, TR=7.8ms, readout frequency=191.7Hz, image size = 224x224, resolution=1x1x3mm^3. An adiabatic inversion pulse is used at the beginning of the sequence for better T1 encoding. The scan time is 8.8 seconds.

Fig.2. T1, T2 and PD maps reconstructed from simulation datasets (SNR = 20) using no RF phase modulation sequence and RF phase modulated sequence with MR-STAT reconstruction. Absolute relative error maps are shown and MAPEs (mean absolute percentage error) are computed. We observe that data using RF phase encoding result in ~50% lower errors in T2 and PD maps.

Fig.3. Gel phantom results using the no RF phase sequence and RF phase modulated sequence. (a) T1 and T2 maps using both sequences. (b) Bar plots with mean T1 and T2 values as well as standard deviations for each gel phantom. Note that results from RF phase modulated sequence show lower standard deviations for T2.

Fig. 4. In-vivo results using the no RF phase sequence and RF phase modulated sequence. It can be observed that T2 and proton density (PD) maps from RF phase modulated sequence show better contrast (black arrow for example) and lower noise. Lower values of CSF and the blood vessel (red arrow) are also observed in T2 maps using the RF modulated sequence.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

0625

DOI: https://doi.org/10.58530/2022/0625