0623

Rapid quantitative magnetization transfer imaging: utilizing the hybrid state and the generalized Bloch model
Jakob Assländer1,2, Cem Gultekin3, Xiaoxia Zhang1,2, Quentin Duchemin4, Kangning Liu5, Robert WE Charlson6, Timothy Shepherd1, Carlos Fernandez-Granda3,5, and Sebastian Flassbeck1,2
1Center for Biomedical Imaging, New York University School of Medicine, New York, NY, United States, 2Center for Advanced Imaging Innovation and Research, New York University School of Medicine, New York, NY, United States, 3Courant Institute of Mathematical Sciences, New York University, New York, NY, United States, 4Laboratoire d’analyse et de mathématiques appliquées, Université Gustave Eiffel, Paris, France, 5Center for Data Science, New York University, New York, NY, United States, 6Multiple Sclerosis Comprehensive Care Center, Department of Neurology, New York University School of Medicine, New York, NY, United States

Synopsis

We combine two recently proposed biophysical models, the hybrid state and the generalized-Bloch model, to describe magnetization transfer. Combined into a single model, they facilitate quantitative magnetization transfer imaging of the whole brain with 1mm isotropic resolution in 12 minutes. We optimized an MR-Fingerprinting-like pulse sequence, and validated the approach in two multiple sclerosis patients and two controls.

Introduction

Quantitative magnetization transfer (qMT) promises high sensitivity and specificity to distinct biological changes in neurodegenerative disease, such as multiple sclerosis (MS).1,2,3 Yet, low spatial resolution and long scan times have, so far, prevented its broad clinical application. Towards overcoming these limitations, we combine two recently proposed biophysical models4,5 in a Bloch-McConnell equation and utilize this joint model to numerically optimize an MR-Fingerprinting-like pulse sequence for qMT imaging of the whole brain with 1mm isotropic resolution in 12min.

Theory

Based on Henkelman's two-pool model,6 we describe the magnetization $$$(x^f,y^f,z^f)^T$$$ of all water-bound protons in the so-called free pool, and the magnetization $$$(x^s,z^s)^T$$$ of all protons bound in large molecules in the so-called semi-solid pool. The coupled dynamics of these two pools are described by$$\partial_t\begin{pmatrix}x^f\\y^f\\z^f\\x^s\\z^s\\1\end{pmatrix}=\begin{pmatrix}-R_2^f&-\omega_z&\omega_y&0&0&0\\\omega_z &-R_2^f&0&0&0&0\\-\omega_y &0&-R_1-R_{\text{x}}m_0^s&0&R_{\text{x}}m_0^f&m_0^fR_1\\0&0&0&-R_2^{s,l}(R_2^s,\alpha,T_\text{RF})&\omega_y&0\\0&0&R_{\text{x}} m_0^s&-\omega_y&-R_1-R_{\text{x}}m_0^f&m_0^sR_1\\0&0&0&0&0&0\end{pmatrix}\begin{pmatrix}x^f\\y^f\\z^f\\x^s\\z^s\\1\end{pmatrix},$$where the Rabi and Larmor frequencies $$$\omega_{x,y,z}$$$ control relaxation and the exchange of longitudinal magnetization between the two pools. The size of the semi-solid and free pool are denoted by $$$m_0^s$$$ and $$$m_0^f=1-m_0^s$$$, respectively. We assume an apparent $$$R_1$$$ relaxation rate that jointly describes both spin pools7 and describe the pools' transversal relaxation rates separately by $$$R_2^{f,s}$$$. The exchange rate is denoted by $$$R_{\text{x}}$$$.

We modified a bSSFP sequence8 to subscribe a train of rectangular RF-pulses with slowly varying flip angles and pulse durations. This drives the free pool into a hybrid state,4 which enables an efficient encoding of biophysical parameters while maintaining the beneficial spin-echo nature of bSSFP sequences.8,9

The semi-solid pool is here described by the generalized-Bloch model, which facilitates an accurate description of spin pools with, e.g., super-Lorentzian lineshapes during short RF-pulses.5 More precisely, we use the model's linear approximation, which re-formulates it into the form of the original Bloch equations with an effective transversal relaxation rate $$$R_2^{s,l}(R_2^s,\alpha,T_\text{RF})$$$ that, in addition to $$$R_2^s$$$ also depends on the flip angle $$$\alpha$$$ and the pulse duration $$$T_\text{RF}$$$.5 Note that we neglect the $$$y$$$-component of the semi-solid pool due to its rapid transversal relaxation ($$$R_2^s\gg\omega_z$$$).

Methods

Pulse sequence optimization: We numerically optimized $$$\alpha$$$ and $$$T_\text{RF}$$$ of 1141 RF-pulses, which are applied in a loop, interleaved with a rectangular inversion pulse.10,4 We minimized the Cramer-Rao bound11,12 of $$$m_0^s,R_1$$$, and $$$R_2^f$$$ while accounting for all model parameters. To ensure a hybrid-state,4 we penalized fast variations of the flip angle. The resulting control, along with the evoked spin dynamics, are sketched in Fig. 1.

k-Space encoding: While looping through the optimized pulse train 189 times, we acquire k-space with a 3D radial koosh-ball trajectory with 2D-golden angle13 increments in the following order: the first time frame is acquired with the first 189 golden angle increments and so forth. Without changing the overall k-space coverage of each time frame, we reshuffled the spokes' order to reduce eddy current artifacts.14

Image reconstruction and model fitting: We reconstructed the highly undersampled data directly in a low-rank space.15,16,17 The resulting coefficient images are virtually artifact free. Further, we trained a neural network to map from the coefficients to the model parameters.18

Experimental setup: We imaged a custom MT phantom containing different concentrations of thermally cross-linked bovine serum albumin (BSA), two remitting-relapsing MS patients, and two controls. Based only on a FLAIR and MP-RAGE, a neuroradiologist drew regions of interest (ROI) in FLAIR lesions with little-to-no hypointensity on the MP-RAGE, and in lesions with a more pronounced $$$T_1$$$-hypointensity.

Results

In the BSA phantom, we find good agreement between the established IR-GRE and proposed qMT sequence (Fig. 2). In vivo, we first assessed the capability of our approach to correct for $$$B_0$$$ and $$$B_1$$$ inhomogeneities and found that $$$B_0$$$ is corrected well outside the banding artifact, and that $$$B_1$$$ is also corrected for, but with more limited precision (Fig. 3).

Fig. 4 depicts good discrimination of MS lesions from normal appearing white matter (NAWM). It further shows good contrast between different lesions: $$$m_0^s$$$ differs substantially between lesion 1 and lesions 2/3, while lesion 3 shows distinct relaxation characteristics. Additionally, lesion 3 is sharply delineated from NAWM, while lesions 1 and 2 are sharply delineated only in $$$m_0^s$$$, and exhibit a gradient-ring in the relaxometry maps. This variability in the MS lesions is also reflected in the ROI analysis (Fig. 5), which additionally alludes to slight differences in the NAWM of the MS patients and controls. However, a clear distinction is currently hampered by residual $$$B_1$$$ artifacts. Further, the most pronounced and most relevant changes in NAWM are expected for secondary-progressive MS, which was not studied here.

Discussion and Conclusion

We demonstrated the viability of qMT with a clinically-feasible protocol (whole brain coverage with 1mm isotropic resolution in 12min). Several developments facilitated such high scan efficiency: first, we used biophysical models that were tailored to rapid and dynamic imaging. Second, we optimized the RF-pulse train and the k-space encoding to improve efficiency and reduce artifacts. Third, we tailored a data-processing pipeline to handle severely undersampled, dynamic data with computational efficiency. Future work will include improvements of the $$$B_1$$$ correction; and challenging the assumptions made in the model. Foremost, it has recently been suggested that $$$R_1$$$ of the semi-solid pool is much faster compared to the free pool.19,20,21 Further, we will scan patients with secondary-progressive MS to study potential changes in NAWM.22,23

Acknowledgements

This research was supported by the grant NIH/NIBIB R21 EB027241 and was performed under the rubric of the Center for Advanced Imaging Innovation and Research, a NIBIB Biomedical Technology Resource Center (NIH P41 EB017183).

References

  1. Stanisz GJ, Webb S, Munro CA, Pun T, Midha R. MR properties of excised neural tissue following experimentally induced inflammation. Magn. Reson. Med. 2004; 51(3): 473–479. doi: 10.1002/mrm.20008
  2. Thiessen JD, Zhang Y, Zhang H, et al. Quantitative MRI and ultrastructural examination of the cuprizone mouse model of demyelination. NMR Biomed. 2013; 26(11): 1562–1581. doi: 10.1002/nbm.2992
  3. Enzinger C, Barkhof F, Ciccarelli O, et al. Nonconventional MRI and microstructural cerebral changes in multiple sclerosis. Nat. Rev. Neurol. 2015; 11(12): 676–686. doi: 10.1038/nrneurol.2015.194
  4. Assländer J, Novikov DS, Lattanzi R, .Sodickson DK, Cloos MA. Hybrid-state free precession in nuclear magnetic resonance. Nat. Commun. Phys. 2019; 2(1): 73. doi: 10.1038/s42005-019-0174-0
  5. Assländer J, Gultekin C, Flassbeck S, Glaser SJ, Sodickson DK. Generalized Bloch model: a theory for pulsed magnetization transfer. Magn Reson Med 2021: doi: 10.1002/mrm.29071.
  6. Henkelman RM, Huang X, Xiang QSS, Stanisz GJ, Swanson SD, Bronskill MJ. Quantitative Interpretation of Magnetization Transfer. Magn. Reson. Med. 1993; 29(6): 759–766.
  7. Dortch RD, Li K, Gochberg DF, et al. Quantitative magnetization transfer imaging in human brain at 3 T via selective inversion recovery. Magn. Reson. Med. 2011; 66(5): 1346–1352. doi: 10.1002/mrm.22928
  8. Carr H. Steady-State Free Precession in Nuclear Magnetic Resonance. Phys. Rev. 1958; 112(5): 1693–1701. doi: 10.1103/Phys-Rev.112.1693
  9. Scheffler, K., & Hennig, J. (2003). Is TrueFISP a gradient-echo or a spin-echo sequence? Magnetic Resonance in Medicine, 49(2), 395–397. https://doi.org/10.1002/mrm.10351
  10. Gochberg DF, Gore JC. Quantitative imaging of magnetization transfer using an inversion recovery sequence. Magn. Reson. Med. 2003; 49(3): 501–505. doi: 10.1002/mrm.10386
  11. Rao CR. Information and the Accuracy Attainable in the Estimation of Statistical Parameters. Bull. Calcutta Math. Soc. 1945; 37(3): 81–91.
  12. Cramér H. Methods of mathematical statistics. Princeton, NJ: Princeton University Press . 1946.
  13. Chan RW, Ramsay EA, Cunningham CH, Plewes DB. Temporal stability of adaptive 3D radial MRI using multi-dimensional golden means. Magn. Reson. Med. 2009; 61(2): 354–363. doi: 10.1002/mrm.21837
  14. Flassbeck S, Assländer J. Minimization of Eddy Current Related Artefacts in HSFP Sequences. In: Proc. Intl. Soc. Mag. Reson. Med.29. ; 2021: 1560.
  15. McGivney D, Ma D, Saybasili H, Jiang Y, Griswold M. Singular Value Decomposition for Magnetic Resonance Fingerprinting in the Time Domain. IEEE Trans. Med. Imaging 2014; 33(12): 2311–2322.
  16. Tamir JI, Uecker M, Chen W, et al. T2 shuffling: Sharp, multicontrast, volumetric fast spin-echo imaging. Magn. Reson. Med. 2017; 77(1): 180–195. doi: 10.1002/mrm.26102
  17. Assländer J, Cloos MA, Knoll F, Sodickson DK, Hennig J, Lattanzi R. Low rank alternating direction method of multipliers reconstruction for MR fingerprinting. Magn. Reson. Med. 2018; 79(1): 83–96. doi: 10.1002/mrm.26639
  18. Zhang X, Duchemin Q, Liu K, et al. Cramer-Rao bound-informed training of neural networks for quantitative MRI. 2021: ArXiV ID: 2109.10535.
  19. Helms G, Hagberg GE. In vivo quantification of the bound pool T1 in human white matter using the binary spinbath model of progressive magnetization transfer saturation. Phys. Med. Biol. 2009; 54(23): N529–N540. doi: 10.1088/0031-9155/54/23/N01
  20. Gelderen vP, Jiang X, Duyn JH. Effects of magnetization transfer on T1 contrast in human brain white matter. Neuroimage 2016; 128: 85–95. doi: 10.1016/j.neuroimage.2015.12.032
  21. Samsonov A, Field AS. Confounding of Macromolecular and Paramagnetic Tissue Content in Quantitative MTI Remedied by Explicit Estimation of Bound Pool Relaxation. In: Proc. Intl. Soc. Mag. Reson. Med. 29. ; 2021: 0716.
  22. Ontaneda D, Fox RJ. Imaging as an Outcome Measure in Multiple Sclerosis. Neurotherapeutics 2017; 14(1): 24–34. doi: 10.1007/s13311-016-0479-6
  23. Mallik S, Samson RS, Wheeler-Kingshott CAM, Miller DH. Imaging outcomes for trials of remyelination in multiple sclerosis. J. Neurol. Neurosurg. Psychiatry 2014; 85(12): 1396–1404. doi: 10.1136/jnnp-2014-307650

Figures

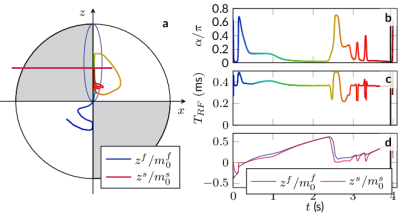
Fig. 1: Spin trajectory and the corresponding control. a The dynamics of the free pool on the Bloch sphere with the steady-state ellipse in blue; b the flip angle α; c the pulse duration control this spin dynamics; d the normalized z-magnetization of the two pools.

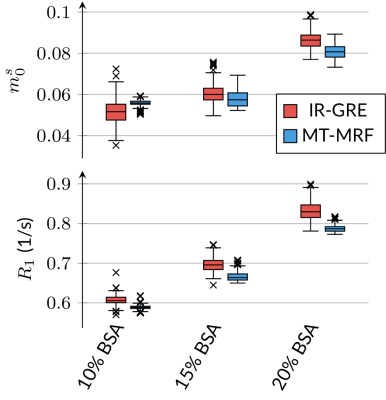
Fig. 2: Validation of the qMT parameters m0s and R1 in a custom build phantom that consists of tubes with different concentrations of thermally cross-linked bovine serum albumin (BSA). We compare the proposed qMT sequence to the established, but slow inversion-recovery gradient recalled echo (IR-GRE) sequence10 and find good agreement.

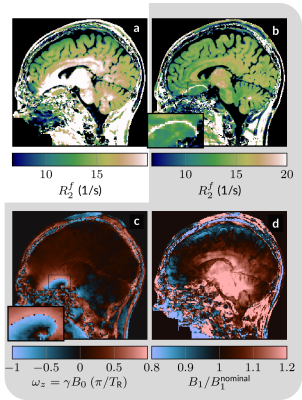
Fig. 3: B0- and B1-correction. a The estimated R2f is biased when assuming homogeneous magnetic fields. b The qMT sequence was designed to estimate B0 and B1, which allows for removal of the bias with the exception of the few voxels in the center of the banding artifact (over the anterior skull base). c,d B0 and B1 estimated from the qMT data. The gray background groups the parameters that were jointly estimated (along with the other 5 parameters).

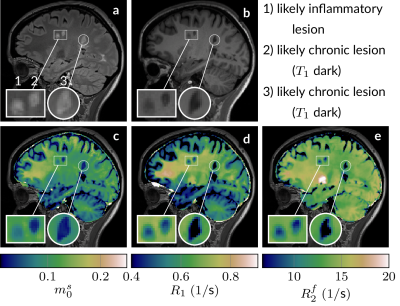
Fig. 4: a A FLAIR, b an MP-RAGE, and c-e qMT maps of an MS patient. The magnifications highlight three lesions that have the same hyperintense appearance on the FLAIR, but show distinct characteristics on quantitative maps, which suggests that qMT distinguishes different lesion types. See Fig. 5 for a quantitative analysis of the lesions.

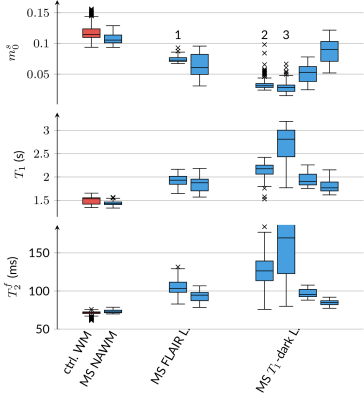
Fig. 5: ROI analysis composed of the median (line), the 0.25-0.75-quartile (box), and the total data range, limited by the 0.25/0.75-quartile ±1.5 interquartile range (whiskers). Outliers are marked by "x." The first two columns show m0s, T1=1/R1, and T2f=1/R2f in normal-appearing white matter (NAWM) regions pooled over all subjects. The other 2 paired columns show MS lesions of patients that are FLAIR-bright, T1-isointense and FLAIR-bright, T1 dark, respectively. All ROIs are located in the centrum semiovale. The numbers 1-3 refer to respective lesions shown in Fig. 4.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)
0623
DOI: https://doi.org/10.58530/2022/0623