0562
Visualizing Encoding Efficiency of MR Fingerprinting Sequences using Leave-One-Out Perturbation (LOOP)1ETH and University Zurich, Zurich, Switzerland
Synopsis
In Magnetic Resonance Fingerprinting, the accuracy of the results is dominated by undersampling artifacts. While in classical relaxometry techniques, the omission of data always leads to a larger error, in fingerprinting, undersampling artifacts can lead to both an increase or a decrease in error. The “temporal encoding efficiency” of fingerprinting can be analyzed based on the change in matching error upon omission of a single time point (leave-one-out). We propose a first-order perturbation of the undersampling error to visualize and identify temporal sequence segments of primary parameter encoding and apply these insights to shorten an exemplary MRF sequence by truncation.
Introduction
In Magnetic Resonance Fingerprinting (MRF),1 parameter estimation accuracy is dominated by undersampling artifacts. While in classical relaxometry techniques, the omission of data always leads to a larger error, in fingerprinting, undersampling artifacts can lead to both an increase or a decrease in error. This “temporal encoding efficiency” can be analyzed by the change in matching error upon omission of a single time point (leave-one-out). To accelerate the analysis, we propose a first-order perturbation of the undersampling error approximation by Stolk and Sibrizzi.2 The analysis is used to identify temporal sequence segments of primary parameter encoding and, based on the insight, to subsequently shorten an exemplary MRF sequence by truncation.Methods
The leave-one-out (LOO) match$$$\;\mathbf{\hat{\theta}}_i^{LOO}\left(\mathbf{x}\right)\;$$$upon omission of time point$$$\;t_i\;$$$during matching is defined by$$\mathbf{\hat{\theta}}_i^{LOO}\left(\mathbf{x}\right)=\text{arg}\max_{\mathbf{\theta}}\sum_{n=1}^N\left|I_n\left(\mathbf{x}\right)-S\left(t_n;\mathbf{\theta}\right)\right|^2-\left|I_i\left(\mathbf{x}\right)-S\left(t_i;\mathbf{\theta}\right)\right|^2,\qquad\text{(Eq. 1)}$$where$$$\;N\;$$$is the number of time points in the MRF sequence,$$$\;I_n\left(\mathbf{x}\right)\;$$$the reconstructed images, and$$$\;S\left(t_i;\mathbf{\theta}\right)\;$$$the signal model for each acquisition time point$$$\;t_i\;$$$and parameter vector$$$\;\mathbf{\theta}\;$$$(here$$$\;\mathbf{\theta}=\left(\log{T1},\log{T2},\rho\right)$$$). As a measure for temporal encoding efficiency, we use the change in normalized root-mean-square error$$$\;\Delta{}nRMSE_i\;$$$between matching with the full sequence$$$\;\mathbf{\hat{\theta}}\left(\mathbf{x}\right)\;$$$and each LOO match$$$\;\mathbf{\hat{\theta}}_i^{LOO}\left(\mathbf{x}\right)\;$$$(Figure 1)$$\Delta{}nRMSE_i=\sqrt{\left\langle\left(\frac{\hat{\mathbf{\theta}}^{LOO}_i\left(\mathbf{x}\right)-\mathbf{\theta}^{GT}\left(\mathbf{x}\right)}{\mathbf{\theta}^{GT}\left(\mathbf{x}\right)}\right)^2\right\rangle_\mathbf{x}}-\sqrt{\left\langle\left(\frac{\hat{\mathbf{\theta}}\left(\mathbf{x}\right)-\mathbf{\theta}^{GT}\left(\mathbf{x}\right)}{\mathbf{\theta}^{GT}\left(\mathbf{x}\right)}\right)^2\right\rangle_\mathbf{x}},$$with ground truth parameters$$$\;\mathbf{\theta}^{GT}\left(\mathbf{x}\right)\;$$$and$$$\;\langle\cdots\rangle_\mathbf{x}\;$$$denoting the mean over all spatial positions$$$\;\mathbf{x}$$$.Equation (1) can be solved by iterating over all points in the sequence and performing matching with an adapted dictionary (LOO-Match). Using the approach by Stolk & Sibrizzi,2 the matching result$$$\;\hat{\mathbf{\theta}}\;$$$can be approximated to first order using the acquisition’s point-spread function (PSF), the signal$$$\;S\left(t;\mathbf{\theta}_0\right)$$$, and its derivatives$$$\;\mathbf{D}_\mathbf{\theta}S\left(t;\mathbf{\theta}_0\right)\;$$$at an expansion point$$$\;\mathbf{\theta}_0$$$. Equally, an approximate solution to (1) can be obtained for each omitted time point (LOO-Stolk).
Considering the LOO problem as a small perturbation to the overall least-squares problem, we can perform a formal perturbation expansion of$$$\;\mathbf{\hat{\theta}}_i^{LOO}\left(\mathbf{x}\right)\;$$$to first-order in$$$\;\epsilon\;$$$(LOO-Perturbation, LOOP) by making use of Stolk’s analytical approximation$$\mathbf{\hat{\theta}}_i^{LOO}\left(\mathbf{x}\right)=\text{arg}\max_{\mathbf{\theta}}\sum_{n=1}^N\left|I_n\left(\mathbf{x}\right)-S\left(t_n;\mathbf{\theta}\right)\right|^2-\epsilon\left|I_i\left(\mathbf{x}\right)-S\left(t_i;\mathbf{\theta}\right)\right|^2$$ $$\approx\hat{\mathbf{\theta}}^{Stolk}\left(\mathbf{x}\right)+\epsilon\Delta\hat{\mathbf{\theta}}^{LOOP}_i\left(\mathbf{x}\right)+O\left(\epsilon^2\right),$$defining$$\hat{\mathbf{\theta}}^{LOOP}_i\left(\mathbf{x}\right)=\hat{\mathbf{\theta}}^{Stolk}\left(\mathbf{x}\right)+\Delta\hat{\mathbf{\theta}}_i^{LOOP}\left(\mathbf{x}\right).$$
In the classical encoding regime, the Cramér-Rao lower bound is an estimator for the noise-dependent parameter encoding error. For comparison, we report its relative change alongside ΔnRMSE.
As an example, a FISP-MRF3,4 sequence with constant repetition time of 15 ms was simulated using the extended phase graph formalism.5 For acquisition, two interleaves of a 40-fold undersampled Archimedean spiral (6 ms duration) were reconstructed on a 128x128 grid. The numerical phantoms were generated with the same resolution deliberately committing the “inverse crime”6 such that matching errors were not biased by downsampling errors. To evaluate the exact LOO-Match, a MRF dictionary was generated on a logarithmic T1/T2 scale with 0.5% T1 and 1% T2 resolution and 63 220 atoms. In each iteration, one dictionary element was omitted and the dictionary re-normalized.
To analyze the sequence encoding efficiency and its dependency on the sampled object, 20 brains from the Brain Web Database (www.bic.mni.mcgill.ca/brainweb/) were randomly sliced to form 128 slices with randomized T1/T2 values with a maximal parameter variation of 25% to remain within the linearizable signal regime.
Results & Discussion
Figure 2 shows the leave-one-out comparison of ΔnRMSE for the exact dictionary matching, Stolk’s approximation, and our perturbation approach using a checkerboard phantom (see Ref. 2). Calculation of the LOO analysis took 60 minutes using dictionary matching, 10 minutes using Stolk’s approximation and 5 seconds employing our perturbation expansion. Our perturbation approach is in very good agreement with Stolk’s approximation and follows closely the matching approach.Figure 3 shows an animation of the statistical analysis that is generating the full LOO results shown in Figure 4a. Integrating Figure 4a over time (Figure 4b), allows to study cancellation effects between subsequent time points. Constant regions in Figure 4b can be interpreted as intervals of no or little parameter encoding. Colored areas denote changing regions and coincide with strong parameter encoding.
Compared to the CRB, ΔnRMSE can be both positive and negative, thus omission of time points during the matching process can be beneficial for removing undersampling artifacts from the final parameter maps. This is contrary to classical encoding regimes, here represented by the CRB, where omission of data always leads to an increase in matching error.
Using the LOO findings of Figure 4 it becomes apparent that encoding is sufficient for T1 after approximately 4 seconds, T2 after 5 seconds, and proton density after ~6 seconds. Hence, the sequence can be considerably shortened if small matching errors are tolerated. In Figure 5, dictionary matching results obtained after truncation of the sequence are shown. Truncation of the sequence from 7.5s per interleave to 5s results in an increase of 10% in nRMSE for T2 and proton density, while T1 remains unchanged. Further truncation of the sequence results in increasing reconstruction error, which is in qualitative agreement with our LOO-Perturbation analysis.
Conclusion
In this work, we have introduced a method to visualize parameter encoding in MR fingerprinting on a temporal basis and proposed a fast way to evaluate it using perturbation theory. The findings can be directly used to compare sequences, identify key encoding time points, and perform truncation in cases where encoding is prematurely finished.Acknowledgements
No acknowledgement found.References
1. Ma, D. et al. Magnetic resonance fingerprinting. Nature 495, 187–192 (2013).
2. Stolk, C. C. & Sbrizzi, A. Understanding the Combined Effect of ${k}$ -Space Undersampling and Transient States Excitation in MR Fingerprinting Reconstructions. IEEE Trans. Med. Imaging 38, 2445–2455 (2019).
3. Jiang, Y., Ma, D., Seiberlich, N., Gulani, V. & Griswold, M. a. MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout. Magn. Reson. Med. 74, 1621–1631 (2015).
4. Sommer, K. et al.
Towards predicting the encoding capability of MR fingerprinting sequences. Magn.
Reson. Imaging 41, 7–14 (2017).
5. Weigel, M. Extended phase graphs: Dephasing, RF pulses, and echoes - pure and simple. J. Magn. Reson. Imaging 41, 266–295 (2015).
6. Guerquin-Kern, M., Lejeune, L., Pruessmann, K. P. & Unser, M. Realistic Analytical Phantoms for Parallel Magnetic Resonance Imaging. IEEE Trans. Med. Imaging 31, 626–636 (2012).
Figures
Figure 1 - Concept of the Leave-One-Out (LOO) Error Metric: A time point’s influence on the parameter map error can be determined by omitting it during matching (LOO-Match). The LOO-Match can be approximated using the approach proposed by Stolk & Sibrizzi (LOO-Stolk). We propose to treat LOO as a small perturbation and perform an expansion of Stolk’s formalism (LOO-Perturbation). As a measure of temporal encoding efficiency, we report the change in normalized root-mean-square error (ΔnRMSE) compared to the match without omission for each time point and parameter (only T1 is shown).
Figure 2 - Validation: Comparison of the change in normalized root mean square error (ΔnRMSE) upon omission of one time point (leave-one-out; LOO) using dictionary matching (LOO-Match), evaluation of Stolk’s approximate formalism (LOO-Stolk), and our LOO-Perturbation approach.
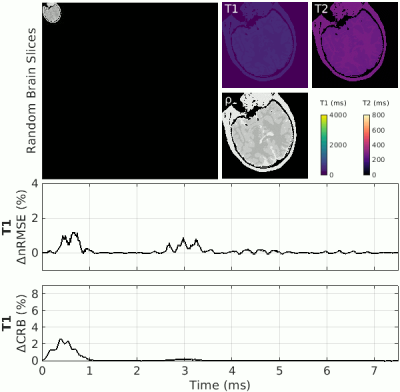
Figure 3 (Animation) – Concept of the Statistical Analysis: The perturbation analysis is repeated for randomly sliced brain geometries with randomized T1/T2 values (T1=30...4000ms, T2=15...800ms). For each parameter and random brain, the ΔnRMSE and the change in Cramer-Rao Lower Bound (ΔCRB) are plotted to signify their dependency on the sampled object. The CRB depicts the matching error in the classical encoding (Gaussian noise) regime. N.B.: While the ΔCRB is always positive, i.e. omission of a time point leads to an increase in error, ΔnRMSE can be both positive or negative.
Figure 4 – Leave-One-Out (LOO) Analysis Results: (A) Change in nRMSE and CRB upon omission of one time point during matching (LOO). Each line corresponds to one of 128 random brain slices. While the change in CRB is always positive, ΔnRMSE can also become negative allowing for cancellation of errors or a reduction in matching error, if data points are omitted during reconstruction. (B) The normalized integrals show regions of error cancellation for ΔnRMSE. In constant areas (white) minor encoding takes place, whereas pronounced slopes denote regions of strong encoding power (colored).
Figure 5 – MRF Truncation Study: Based on the encoding regions identified in Figure 4, the MRF sequence can be truncated from the end, shortening the acquisition duration with a controlled increase in matching error. The numbers indicate the change in nRMSE compared to the untruncated sequence (4).