0514
Fast acquisitions for mean kurtosis and microscopic fractional anisotropy1Center for Advanced Imaging Innovation and Research (CAI2R), Department of Radiology, New York University, School of Medicine, New York, NY, United States, 2Department of Diagnostic Radiology, Clinical Sciences, Lund University, Lund, Sweden
Synopsis
We propose two acquisition protocols that minimize the number of directions needed for estimating MD, FA, MK, and $$$\mu$$$FA. Using symmetric trace-free decompositions of the diffusion, kurtosis, and covariance tensors, we design acquisitions that cancel unnecessary tensor elements, thereby reducing the number of directions needed to generate the maps. Our protocols consist of $$$3b_1+6b_2=9$$$ DWIs for MD+MK in a 1-minute scan, and $$$6b_1^\text{LTE}+6b_2^\text{LTE}+3b_{1.5}^\text{STE}=15$$$ DWIs for MD+FA+MK+$$$\mu$$$FA in a 2-minute scan. We show the feasibility of these approaches on a healthy volunteer.
Introduction
Diffusion Kurtosis Imaging (DKI) is a widespread representation for the diffusion MRI signal up to intermediate b-values1. The diffusion and kurtosis tensors, $$$\boldsymbol{D}$$$ and $$$\boldsymbol{W}$$$, have 6 and 15 independent components, respectively. However, typical analyses do not look at individual tensor elements but combine them to generate contrasts like mean diffusivity (MD), fractional anisotropy (FA) and mean kurtosis (MK).Tensor-valued diffusion encoding lets us probe a more general tensor than kurtosis, the diffusion covariance $$$\boldsymbol{C}$$$2. This has 21 independent components and captures the necessary information for generating MK and additional contrasts such as microscopic fractional anisotropy ($$$\mu$$$FA)2,3,4,5.
Interestingly, not all elements in $$$\boldsymbol{D}$$$ and $$$\boldsymbol{C}$$$ are necessary for generating the contrasts mentioned above. By representing these tensors in Symmetric Trace-Free (STF) basis we can separate the contributions to MD, FA, MK, and $$$\mu$$$FA. Furthermore, using the relation between spherical harmonics and STF tensors, we develop two minimal acquisitions targeted at measuring MD+MK and MD+FA+MK+$$$\mu$$$FA. These acquisitions cancel the contributions of tensor elements unnecessary for generating such maps. Our acquisitions minimize the number of measurements, neither compromising accuracy nor introducing extra assumptions. We acquired our protocols in a healthy volunteer and compared our results against estimates from a comprehensive protocol with 10X more measurements. We show that it is feasible to measure a full brain at $$$2\times2\times2$$$mm$$$^3$$$ resolution on a clinical scanner and obtain MD+MK with 9 DWI (1-minute scan) and MD+FA+MK+$$$\mu$$$FA with 15 DWI (2-minute scan).
Theory
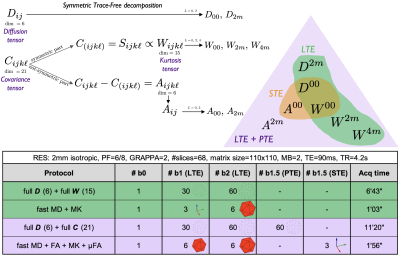
The cumulant expansion $$$\mathcal{O}(b^2)$$$ for linear tensor encoding (LTE) is1:$$\log(S)=\log(s_0)-b\,\sum_{ij}n_in_j\,D_{ij}+\tfrac16b^2\overline{D}^2\,\sum_{ijk\ell}n_in_jn_kn_\ell\,\!W_{ijk\ell},\qquad(1)$$where $$$\boldsymbol{D}$$$ and $$$\boldsymbol{W}$$$ are the diffusion and kurtosis tensors and $$$\overline{D}=\text{tr}\,\boldsymbol{D}$$$. These tensors are symmetric and, thus, can be represented in STF basis $$$\mathcal{Y}_{i_1...i_\ell}^{\ell\,\!m}$$$6:$$D_{ij}=D_{00}\tfrac{1}{\sqrt{4\pi}}\delta_{ij}+\sum_{m=-2}^2D_{2m}\mathcal{Y}_{ij}^{2m},\quad\,\!W_{ijk\ell}=W_{00}\tfrac{1}{\sqrt{4\pi}}\delta_{(ij}\delta_{k\ell)}+\sum_{m=-2}^2W_{2m}\mathcal{Y}_{(ij}^{2m}\delta_{k\ell)}+\sum_{m=-4}^4W_{4m}\mathcal{Y}_{ijk\ell}^{4m},\qquad(2)$$where $$$\delta_{ij}$$$ is Kronecker's delta, and symmetrization over tensor indices between (...) is assumed. This basis is analogous to spherical harmonics and for every order $$$\ell$$$ we can define rotational invariants7,8, e.g. $$$W_\ell=\sqrt{\frac{\sum_m|W_{\ell\,\!m}|^2}{4\pi(2\ell+1)}}$$$.Assuming multiple Gaussian compartments, we can extend Eq. 1 to a general multidimensional dMRI acquisition:2$$\log(S)=\log(s_0)-\sum_{ij}B_{ij}\,D_{ij}+\tfrac12\sum_{ijk\ell}B_{ij}B_{k\ell}C_{ijk\ell},\qquad(3)$$where $$$\boldsymbol{B}$$$ is the measurement b-tensor and $$$\boldsymbol{C}$$$ is the 21-parameter diffusion covariance tensor whose fully-symmetric part is proportional to $$$\boldsymbol{W}$$$. Since $$$\boldsymbol{C}$$$ is not fully symmetric, it is separable into $$$\boldsymbol{W}$$$ (15 independent parameters) and the non-symmetric part $$$\boldsymbol{A}$$$ (6 independent parameters). Figure 1 shows a diagram of this decomposition together with how to probe each part through LTE, planar tensor encoding (PTE), or spherical tensor encoding (STE).
Spherical L-designs are sets of N points on the unit sphere $$$\{\hat{\boldsymbol{n}}_i\}_{i=1}^N$$$ such that$$\tfrac{1}{4\pi}\int_{\mathbb{S}^2}d\hat{\boldsymbol{n}}f(\hat{\boldsymbol{n}})=\tfrac1N\sum_{i=1}^Nf(\hat{\boldsymbol{n}}_i),\,\text{where}\,f(\hat{\boldsymbol{n}})=\sum_{\ell=0}^L\sum_{m=-\ell}^\ell\,\!f_{\ell\,\!m}Y_{\ell\,\!m}(\hat{\boldsymbol{n}}),\qquad(4)$$e.g.$$$\,N=12$$$ icosahedron vertices form a 4-design providing exact average of any spherical harmonics expansion up to $$$L=4$$$.
MD and MK can be derived from the diffusion and kurtosis tensors by:$$\begin{aligned}\text{MD}&=\overline{D}=\tfrac{1}{4\pi}\int_{\mathbb{S}^2}d\hat{\boldsymbol{n}}D(\hat{\boldsymbol{n}})=\tfrac13\sum_{ij}\delta_{ij}D_{ij}=\tfrac{1}{\sqrt{4\pi}}D_{00}=D_0,\qquad\qquad(5)\\\text{MK}&=\overline{W}=\tfrac{1}{4\pi}\int_{\mathbb{S}^2}d\hat{\boldsymbol{n}}W(\hat{\boldsymbol{n}})=\tfrac15\sum_{ijk\,\!\ell}\delta_{ij}\delta_{k\ell}W_{ijk\ell}=\tfrac{1}{\sqrt{4\pi}}W_{00}=W_0.\end{aligned}$$For kurtosis we use a tensor-derived mean (trace)9,10,11, rather than directionally-averaged apparent kurtosis. To construct these maps, we only need the fully isotropic parts $$$D_{00},\,W_{00}$$$, making the estimation of full $$$\boldsymbol{D}$$$ and $$$\boldsymbol{W}$$$ unnecessary. Since their maximal order is $$$L=4$$$, the 4-design is sufficient to yield an unbiased spherical average of $$$\boldsymbol{W}$$$. Antipodal symmetry means only half (i.e. 6) icosahedron directions are needed. Instead of fitting Eq. 1 to the data, we estimate only the isotropic parts of both tensors (using 3 directions for MD and 6 for MK) relying on the orthogonality between terms, Fig.2a. This requires only 3+6=9 DWIs, fewer than previously suggested 12-direction design12.
FA and $$$\mu$$$FA can be written as a function of cumulant invariants:$$\begin{aligned}\text{FA}^2&=\frac32\frac{{V_{\lambda}(\boldsymbol{D})}}{{V_{\lambda}(\boldsymbol{D})}+3\overline{D}^{2}}=\frac{75D_2^2}{4D_0^2+50D_2^2},\qquad\qquad\qquad\qquad\qquad(6)\\\mu\mathrm{FA}^{2}&=\frac32\frac{\langle\,\!V_{\lambda}(\boldsymbol{D})\rangle}{\langle\,\!V_{\lambda}(\boldsymbol{D})\rangle+3\overline{D}^{2}}=\frac{60(S_0-\tfrac12A_0)+675D_2^2}{40(S_0-\tfrac12A_0)+450D_2^2+36D_0^2},\end{aligned}$$where $$$V_{\lambda}(\boldsymbol{D})$$$ is the variance of the eigenvalues of $$$\boldsymbol{D}$$$ and angular brackets denote average over a voxel. For these maps, we need to access $$$D_{00},\,D_{2m},\,S_{00},\,\text{and}\,A_{00}$$$ elements, thus, we do not need the full $$$\boldsymbol{C}$$$. Instead of fitting Eq. 3, we can estimate only the parts we need, see Fig. 2b. We estimate $$$S_{2m}$$$ elements to get unbiased $$$D_{2m}$$$ because $$$b$$$ and $$$b^2$$$ contributions are not orthogonal. Work from13 proposed an acquisition MD+MK+$$$\mu$$$FA in 3 minutes but with lower resolution and number of slices due to requiring more DWI.
MRI experiments
After providing informed consent, a 30yo female volunteer underwent MRI in a whole-body 3T-system (Siemens Prisma) using a 20-channel head coil. Maxwell-compensated free gradient diffusion waveforms were used to yield LTE, PTE, and STE using a prototype spin-echo sequence with EPI readout14. Four diffusion datasets were acquired according to the table in Fig 1. Imaging parameters: voxel size$$$\,=2\times2\times2\,$$$mm$$$^3$$$, $$$T_R=4.2$$$s, $$$T_E=90$$$ms, bandwidth=1818Hz/Px, $$$R_\text{GRAPPA}=2$$$, partial Fourier$$$\,=6/8$$$, multiband$$$\,=2$$$.Results
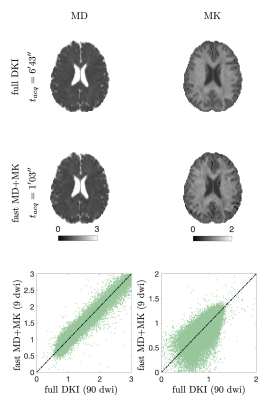
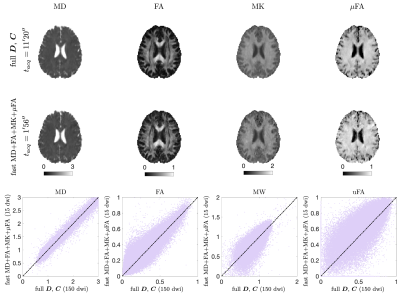
MD and MK estimates from the densely sampled LTE-only protocol and the fast protocol are shown in Fig. 3. Figure 4 shows MD+FA+MK+$$$\mu$$$FA from the densely-sampled LTE+PTE protocol and the fast protocol. In both cases, fast maps showed a very similar contrast to the fully sampled despite having 10-fold fewer measurements.Discussion and Conclusion
We propose here two acquisition protocols that optimize and minimize the number of directions for MD, FA, MK, and $$$\mu$$$FA. Using an STF decomposition of the diffusion, kurtosis, and covariance tensors, we separated the contribution of each tensor element to the parametric maps of interest. By canceling unnecessary contributions we reduce the number of free parameters, allowing the estimation of different contrasts combinations in a faster scan. We proposed minimal acquisitions containing $$$3b_1+6b_2=9$$$ DWI for MD+MK in a 1-minute scan, and $$$6b_1^\text{LTE}+6b_2^\text{LTE}+3b_{1.5}^\text{STE}=15$$$ DWI for MD+FA+MK+$$$\mu$$$FA in a 2-minute scan. We show the feasibility of our fast protocols on a healthy volunteer.Acknowledgements
This work has been supported by NIH under NINDS award R01 NS088040 and NIBIB awards R01 EB027075 and P41 EB017183.References
1. J. H. Jensen, J. A. Helpern, A. Ramani, H. Lu, and K. Kaczynski, “Diffusional Kurtosis Imaging: The quantifica- tion of non-gaussian water diffusion by means of magnetic resonance imaging,” Magnetic Resonance in Medicine, vol. 53, pp. 1432–1440, 2005.
2. C.-F.Westin,H.Knutsson,O.Pasternak,F.Szczepankiewicz,E.O ̈zarslan,D.vanWesten,C.Mattisson,M.Bo- gren, L. J. O’Donnell, M. Kubicki, D. Topgaard, and M. Nilsson, “q-space trajectory imaging for multidimensional diffusion MRI of the human brain,” NeuroImage, vol. 135, pp. 345–362, 2016.
3. S. N. Jespersen, H. Lundell, C. K. Sønderby, and T. B. Dyrby, “Orientationally invariant metrics of apparent compartment eccentricity from double pulsed field gradient diffusion experiments,” NMR in Biomedicine, vol. 26, pp. 1647–1662, 2013.
4. S. Lasiˇc, F. Szczepankiewicz, S. Eriksson, M. Nilsson, and D. Topgaard, “Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion mri with magic-angle spinning of the q-vector,” Frontiers in Physics, vol. 2, p. 11, 2014.
5. F. Szczepankiewicz, D. van Westen, E. Englund, C.-F. Westin, F. St ̊ahlberg, J. L ̈att, P. C. Sundgren, and M. Nilsson, “The link between diffusion MRI and tumor heterogeneity: Mapping cell eccentricity and density by diffusional variance decomposition (DIVIDE),” NeuroImage, vol. 142, pp. 522–532, 2016.
6. K. S. Thorne, “Multipole expansions of gravitational radiation,” Rev. Mod. Phys., vol. 52, pp. 299–339, 1980.
7. M. Reisert, E. Kellner, B. Dhital, J. Hennig, and V. G. Kiselev, “Disentangling micro from mesostructure by diffusion MRI: A Bayesian approach,” NeuroImage, vol. 147, pp. 964 – 975, 2017.
8. D. S. Novikov, J. Veraart, I. O. Jelescu, and E. Fieremans, “Rotationally-invariant mapping of scalar and orien- tational metrics of neuronal microstructure with diffusion MRI,” NeuroImage, vol. 174, pp. 518 – 538, 2018.
9. H. Lu, J. Jensen, A. Ramani, and J. Helpern, “Three-dimensional characterization of non-gaussian water diffusion in humans using diffusion kurtosis imaging,” NMR in Biomedicine, vol. 19, no. 2, pp. 236–247, 2006.
10. B. Hansen, T. E. Lund, R. Sangill, and S. N. Jespersen, “Experimentally and computationally fast method for estimation of a mean kurtosis,” Magnetic Resonance in Medicine, vol. 69, no. 6, pp. 1754–1760, 2013.
11. S. N. Jespersen, J. L. Olesen, B. Hansen, and N. Shemesh, “Diffusion time dependence of microstructural param- eters in fixed spinal cord,” NeuroImage, vol. 182, pp. 329–342, 2017.
12. B. Hansen, T. E. Lund, R. Sangill, E. Stubbe, J. Finsterbusch, and S. N. Jespersen, “Experimental considerations for fast kurtosis imaging,” Magnetic resonance in medicine, vol. 76, no. 5, pp. 1455–1468, 2016.
13. M. Nilsson, F. Szczepankiewicz, J. Brabec, M. Taylor, C.-F. Westin, A. Golby, D. van Westen, and P. C. Sund- gren, “Tensor-valued diffusion mri in under 3 minutes: an initial survey of microscopic anisotropy and tissue heterogeneity in intracranial tumors,” Magnetic Resonance in Medicine, vol. 83, no. 2, pp. 608–620, 2020.
14. F. Szczepankiewicz, C.-F. Westin, and M. Nilsson, “Maxwell-compensated design of asymmetric gradient wave- forms for tensor-valued diffusion encoding,” Magnetic Resonance in Medicine, vol. 0, pp. 1–14, 2019.
Figures