0504
Nonlinear encoding scheme design for gradient-free projection imaging in an inhomogeneous Bo at low-field
Kartiga Selvaganesan1, Yonghyun Ha2, Gigi Galiana2, and Todd Constable2
1Biomedical Engineering, Yale University, New Haven, CT, United States, 2Radiology and Biomedical Imaging, Yale University, New Haven, CT, United States
1Biomedical Engineering, Yale University, New Haven, CT, United States, 2Radiology and Biomedical Imaging, Yale University, New Haven, CT, United States
Synopsis
Gradient-free imaging at low-fields can significantly reduce the cost of and increase access to MRI devices. Here we propose to exploit the Bloch-Siegert shift effect to perform gradient-free, RF spatial encoding at 24mT. We have developed a simulation algorithm that designs various nonlinear encoding schemes and evaluates their performance through image reconstruction. Our results indicate that this technique is tolerant to noise and B0 inhomogeneities; this is an important step towards demonstrating the feasibility of performing low-field imaging with nonlinear RF spatial encoding using the Bloch-Siegert shift.
Introduction
The cost and complexity of MR systems can be significantly reduced by moving towards lower field strengths and eliminating gradients coils. Instead, spatial encoding can be performed using RF coils. One way to perform RF spatial encoding is by using the Bloch-Siegert shift on coils with spatially varying B1-fields, so the off-resonance RF pulse produces a spatially varying phase shift1. Previous work using this method focused on imposing linear phase shifts which is difficult since RF coils produce inherently nonlinear field patterns2. Therefore, we have developed novel nonlinear encoding schemes for gradient free imaging using the Bloch-Siegert shift at low-field (24mT). Here we present the design and evaluation of these schemes through simulation studies.Methods
Figure 1 shows a schematic of the simulation workflow used in this study. From a measured B0-field map, a nonplanar slice containing uniform magnetic field strength (1MHz), was selected as the imaging slice (Figure 1A). Next, the B1-field across the slice profile was calculated for each channel of a 3x3 planar RF transmit (Tx) array. Using these B1-fields, each encoding pattern was calculated using the following equation: $$B_1 = \sum_1^{c = 9} B_1^c \times A^c$$ where $$$A$$$ is the amplitude and phase of the Bloch-Siegert off-resonance pulse applied to each channel (Figure 1B). In this study we evaluated encoding schemes created from unique combinations of 4, 6 or 8 Tx coils, with a pulse phase of either 0 or $$$\pi$$$. The phasor generated by each encoding pattern was then calculated using Bloch simulations. Figure 1C shows examples of unwrapped phasors resulting from transmitting the Bloch-Siegert pulse on 4 and 8 coils. Finally, the MR signal generated by each encoding scheme was used to reconstruct a grid and 3T liver phantom image using the conjugate gradient method for nonlinear encoding fields3 (Figure 1D). Signals were simulated for a spin echo sequence (Figure 1D) implemented with the following parameters: 256 readout points per echo, 128 echoes, 20cmx20cm FOV, TE=16ms, and maximum Bloch-Siegert pulse length=5.88ms. Images were reconstructed over a matrix of 256x256.Results
Figure 2A shows the results from reconstructing a digital grid phantom with data generated from encoding schemes of Tx on 4, 6 and 8 coils. Encoding schemes were optimized to improve reconstruction on a central ROI delineated by the blue box. Figure 2B shows plots of the signal profiles along horizontal (purple) and vertical (green) lines through the center of the FOV for each encoding scheme. The plot in black is the line profile of the phantom image. These results demonstrate that increasing the number of Bloch-Siegert transmit coils can help improve the image resolution within the FOV (blue box).The effect of adding noise to the simulated MR signal prior to reconstruction is shown in Figure 3, with reconstruction results from a liver image extracted from the true position of the simulated slice. Gaussian white noise was added to the signal at SNR levels of 50dB, 25dB, and 10dB. An SNR of 50dB is comparable to noiseless signal, where 25 and 10dB are closer to what is achievable with the physical hardware. The normalized root mean square error (RMSE) and structural similarity index (SSIM) values for these reconstructed images compared to a corresponding 3T liver image are listed in Figure 4.
Since the B1-field strength of RF coils drop with depth, the spatial variation in Bloch-Siegert encoding is to expected decrease with increasing distance from the array coil, though this can be compensated with longer encoding pulses. Figure 5 shows the reconstruction results of a liver image at a 1.4cm and 6.4cm depth, encoded using a 5.88ms and 11.76ms Bloch-Siegert pulse. The results indicate that resolution is recovered when the length of the Bloch-Siegert pulse is doubled.
Discussion
These simulation results support the feasibility of performing gradient-free, nonlinear RF encoding using the Bloch-Siegert shift, on our low-field MRI system. The simulation algorithm developed in this study allows us to robustly design and assess different encoding schemes and evaluate their performance through MR image reconstruction.Overall, the results showed that the quality of the reconstructed images improves by increasing the number of Bloch-Siegert transmit coils. While the system is generally quite tolerant to Gaussian noise, in the case where noise dominates the MR signal (10dB), encoding schemes with Tx on 4 coils outperformed that of 6 and 8 coils. This may be because schemes with fewer transmit coils create regions in the FOV with slower phase windings which are then more tolerant to noise. The results also illustrate that, though the SNR, resolution and contrast are variable across the FOV, the variations are small, and the resulting images have significant diagnostic potential. This characteristic is like that of other imaging methods that incorporate nonlinear spatial encoding at higher fields4,5.
We showed that one way to improve image quality is by increasing the duration of the Bloch-Siegert pulse. To further improve image reconstruction, in the future we will implement deep learning-based image reconstruction techniques6,7.
Conclusion
In this study we have designed and numerically analyzed novel nonlinear RF encoding schemes for gradient free imaging at low-fields. This technique reimagines conventional MR, making it low-cost, noise-free, and highly accessible.Acknowledgements
No acknowledgement found.References
- Bloch, F. and A. Siegert, Magnetic Resonance for Nonrotating Fields. Physical Review, 1940. 57(6): p. 522-527.
- Kartausch, R., et al., Spatial phase encoding exploiting the Bloch-Siegert shift effect. MAGMA, 2014. 27(5): p. 363-71.
- Li, S., et al., Algebraic reconstruction technique for parallel imaging reconstruction of undersampled radial data: application to cardiac cine. Magn Reson Med, 2015. 73(4): p. 1643-53.
- Wang, H., et al., Experimental O-space turbo spin echo imaging. Magnetic resonance in medicine, 2016. 75(4): p. 1654-1661.
- Wang, H., et al., Fast rotary nonlinear spatial acquisition (FRONSAC) imaging. Magn Reson Med, 2016. 75(3): p. 1154-65.
- Koonjoo, N., et al., Boosting the signal-to-noise of low-field MRI with deep learning image reconstruction. Scientific Reports, 2021. 11(1): p. 8248.
- Zhu, B., et al., Image reconstruction by domain-transform manifold learning. Nature, 2018. 555(7697): p. 487-492.
Figures
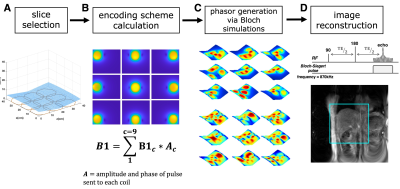
Figure 1. Simulation workflow.
A) A nonplanar 1MHz imaging
slice was selected from the nonuniform electromagnet. B) Encoding schemes were
then created from the B1-fields calculated for each coil element (top), using
the equation shown. C) The phasors produced by each scheme was then calculated
using a Bloch simulation algorithm developed in house. A subset of 9
different phasors is shown, generated from transmitting the Bloch-Siegert off-resonance
pulse on 4 and 8 coils. D) Finally, images encoded with these phasor patterns
were reconstructed using a conjugate gradient technique.
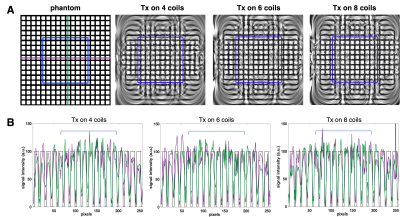
Figure 2. Grid phantom reconstruction.
A) Reconstruction results
of a grid phantom image (left-most) encoded using three different encoding schemes
of transmitting (Tx) the Bloch-Siegert pulse on 4, 6 and 8 coils. Image
reconstruction was performed using 128 encoding patterns over a 256x256 matrix.
The blue box indicates a 20cmx20cm region of interest. B) Plots showing the
signal profile across a horizontal (purple) and vertical (green) line for each
encoding scheme. The black line is the ideal signal profile of the phantom
image.
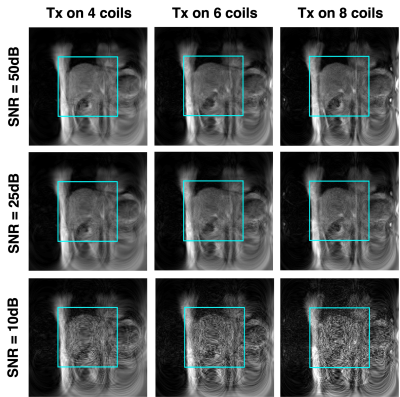
Figure 3. The effect of adding noise.
Liver images reconstructed
using 3 different encoding schemes with varying levels of gaussian white noise
added to the simulated MR signal. Image reconstruction was performed using 128
encodings patterns on a 256x256 matrix. The blue box indicates the center of
the FOV.
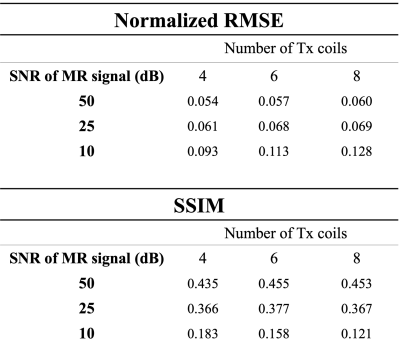
Figure 4. Quantitative analysis.
Table showing the normalized RMSE and SSIM of the
reconstructed liver images (shown in Figure 3) compared to a corresponding 3T
liver image. All values were computed for a 20cmx20cm region of interest in the
center of the FOV.
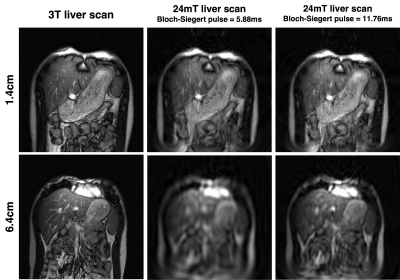
Figure 5. Improving SNR with longer RF pulses.
Simulation results
demonstrating that image quality with depth can be improved by increasing the
duration of the Bloch-Siegert pulse. First column shows the high-resolution
liver phantom images used in the simulation experiments, at a 1.4cm (top row)
and 6.4cm depth (bottom row). Middle column shows the results when the images
were encoded using a Bloch-Siegert pulse with a 5.88ms length, and the last
column shows the results when this pulse length was doubled to 11.76ms.
DOI: https://doi.org/10.58530/2022/0504