0503
SNR-efficient SSFP with k-space aliasing1Department of Brain Sciences, Imperial College London, London, United Kingdom, 2UK Dementia Research Institute Centre for Care Research and Technology, London, United Kingdom, 3MRC London Institute of Medical Sciences, Imperial College London, London, United Kingdom, 4UK Dementia Research Institute Centre at Imperial College London, London, United Kingdom, 5Wellcome Centre for Integrative Neuroimaging, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom, 6Department of Bioengineering, Imperial College London, London, United Kingdom
Synopsis
Steady state free precession (SSFP) imaging with unbalanced gradients (e.g. FISP, PSIF, DESS) causes aliasing in k-space which is often overlooked, or at best, minimised with large spoilers. Here we exploit this phenomenon and use the aliased signals to increase the SNR-efficiency of SSFP imaging.
Introduction
Balanced SSFP (bSSFP) imaging is highly SNR-efficient but suffers from ‘bands’ of reduced signal intensity across the image. The inclusion of gradient spoiling in FISP (or PSIF) eliminates these bands from the reconstructed images but substantially reduces the SNR. Although banding patterns are not observable in FISP images, they still occur at a sub-voxel scale and cause aliasing in k-space. This is a source of confounding but can also be used to give additional information1-2.Here we describe a strategy for improving the SNR efficiency of FISP by exploiting inherent k-space aliasing. We call this kaFISP (k-space aliased FISP).
Theory
k-space aliasing in FISPIn FISP, the characteristic off-resonance banding pattern of bSSFP occurs as a repeating signal modulation along the direction of the unbalanced gradient (Figure 1a, columns i & iii). Typically, the time integral of this gradient is chosen so that the periodicity of the pattern is smaller than the voxel spacing, thus ensuring that undesirable bands are no longer visible. In k-space, this is equivalent to ensuring that the centre of the aliased signals occur outside of the sampled region (Figure 1b).
At high flip angles (α≥40° for grey matter/white matter/CSF at 3T), the banding pattern resembles a sinusoid, with two configuration states (F0 and F-1) contributing approximately equally to the measured signal (Figure 1a, columns ii & iv). Their relative phases can be described in terms of the local ΔB0 and chosen linear RF phase cycling increment (Δφ), which together determine the spatial shifting of the sinusoidal pattern within the voxel. Furthermore, the position of the aliased signal in k-space can be modified by changing the polarity of the unbalanced gradient (Figure 1c).
4-shot kaFISP experiment
This enables, for example, a 4-shot experiment. We acquire 4 acquisitions where we vary Δφ (0, π) and unbalanced gradient polarity (+ve, -ve; Figure 2a). In each acquisition we only acquire the central 1/3 of k-space, containing the aliased signals. We then combine these data to generate the full alias-free k-space (Figure 2b).
This is more SNR-efficient than traditional FISP imaging due to the repeated sampling of the centre of k-space (Figure 3). When the F0 and F-1 signals are approximately equal (which holds for T2>>TR at high α), this provides a potential 34% improvement in SNR efficiency compared to a traditional FISP acquisition.
Accounting for off-resonance: direct reconstruction
The key challenge to the core idea is that off-resonance (ΔB0) introduces non-linear phase terms which must also be included in the forward model. Using a similar approach to Hennel3, we can apply separate ΔB0 phase terms to the F0 and F-1 signals in image space, Fourier transform them, and then shift them to give their k-space representations ($$$S_0$$$ and $$$S_{-1}$$$ respectively):
$$S_0(k)=FT(\beta_0Xe^{2πi∆B_0(x)TE})(k)$$ $$S_{-1}(k)=FT(\beta_{-1}Xe^{-2πi∆B_0(x)TE}e^{-i(∆φ+π)})(k±k')$$ where $$$X$$$ is the image, TE is the echo time, $$$k'$$$ is the k-space shift from the unbalanced gradient, and $$$β$$$ is a scalar signal weighting. At high flip angles (α≥40° in brain at 3T), $$$\beta_0 \approx \beta_{-1}$$$. Therefore, we can reconstruct the full k-space provided we have a separate measurement of ΔB0.
Accounting for off-resonance: iterative reconstruction
Alternatively, we can jointly reconstruct $$$X$$$ and ΔB0 from the data itself, without the need for a separate ∆B0 measurement. The forward operator $$$\mathbb{F}_X$$$ for each aliased dataset $$$d$$$ is:
$$d=\mathbb{F}_XX=SDM\mathscr{F}ΨX$$ where $$$Ψ$$$ combines the phase terms due to ΔB0 (non-linear), Δφ (0 or π) and $$$k'$$$ (+ve or -ve ramp); $$$\mathscr{F}$$$ is the Fourier operator; $$$M$$$ mixes the aliased signals; $$$D$$$ is a down-sampling operator; and $$$S$$$ is the coil sensitivity matrix. Next, we linearise this forward operator in ΔB0 (giving $$$\mathbb{F}_{B}$$$) using Taylor expansion4. Finally, we formulate the joint reconstruction as an alternating minimisation problem, calculating the following at the $$$n$$$th iteration:
$$X^n=argmin_X(\Vert\mathbb{F}_{X}(∆{B_0}^{n-1})X-d\Vert_2^2+\lambda_1\Vert X\Vert_2^2)$$$${∆B_0}^n=argmin_{∆B_0}(\Vert\mathbb{F}_{B}(X^n){∆B_0}-d\Vert_2^2+\lambda_2\Vert {ΔB_0}\Vert_2^2)$$ where $$$λ_1$$$ and $$$λ_2$$$ are regularisation weights, and the initial estimate $$$Δ{B_0}^0$$$ is an array of zeros.
Methods
We performed an experiment on a healthy volunteer on a 3T Magnetom Prisma (Siemens Healthineers, Erlangen, Germany) with a 64ch head coil. We acquired a 3D kaFISP (TR/TE=8.4ms/4.2ms, FA=60°, FOV=250x250x160mm3, four acquisitions with a resolution of 1.0x3.0x1.0mm3 reconstructed to 1.0x1.0x1.0mm3, BW=1kHz/pix, TA=8:11 [2:03 per acquisition]) and a matched 3D FISP (TR/TE=8.4ms/4.2ms, FA=60°, FOV=250x250x160mm3, 1.0x1.0x1.0mm3, BW=1kHz/pix, TA=5:45). Multicoil data were combined using ESPIRiT5. A low-resolution ΔB0 map was acquired from a dual-echo GRE (TR/TE1/TE2=476ms/4.92ms/7.38ms, FA=60°, 2.0x2.0x3.0mm3).Due to the reduced gradient requirements in kaFISP, its readout bandwidth could have also been reduced by a factor of nearly 3 to provide an additional SNR benefit over FISP, or the TR reduced to shorten the scan time to 6:43, but this was not done to ensure images were comparable.
Results & Discussion
kaFISP brain images are shown in Figure 4, alongside the low-resolution acquired data and reference FISP. Direct (Figure 5c) and iterative reconstructions (Figure 5d) are also shown. The former shows residual ringing artifacts from phase inconsistencies between adjacent k-space bands. This is improved via joint reconstruction but could further be improved with a reduced unbalanced gradient area, ensuring overlap between bands3.Conclusions
k-space aliasing is inherent in FISP and should not be ignored, but it can be exploited to give an SNR-efficient acquisition strategy, while also providing a map of B0 inhomogeneity.Acknowledgements
We wish to thank Dr Iulius Dragonu (Siemens Healthineers) for providing advice and support for sequence development. PJL acknowledges generous funding from The Wellcome Trust (220473/Z/20/Z), The Edmond J Safra Foundation, UK Dementia Research Institute, and National Institutes of Health (R01EB002524).References
[1] , , . (2021) Unbalanced SSFP for super-resolution in MRI. Magn Reson Med. 85: 2477– 2489
[2] Lally, PJ, Grech-Sollars, M, Smith, J, Statton, B, et al. (2021) High-resolution, low-SAR 3D T2 relaxometry with COMBINE. Proc. Intl. Soc. Mag. Reson. Med. 29: 4165
[3] Hennel, F, Tian, R, Engel, M, Pruessmann, KP. (2018) In-plane “superresolution” MRI with phaseless sub-pixel encoding. Magn Reson Med. 80: 2384– 2392
[4] Usman, M, Kakkar, L, Matakos, A, Kirkham, A, et al. (2020) Joint B0 and image estimation integrated with model based reconstruction for field map update and distortion correction in prostate diffusion. Magn. Reson. Imaging MRI 65: 90-99
[5] Uecker M, Lai P, Murphy MJ, Virtue P, et al. (2014) ESPIRiT--an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med. Mar;71(3):990-1001
Figures
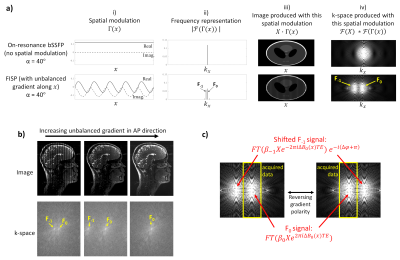
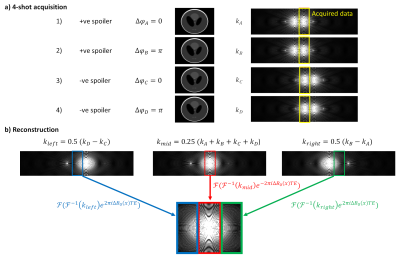
Figure 2: a) Schematic of the 4-shot kaFISP acquisition strategy, with the unbalanced gradient polarity switched between positive and negative, and the phase cycling increment Δφ varied between 0 and π. b) Schematic of the direct reconstruction strategy. The 4 measured signals are combined, inverse Fourier transformed and corrected for spatial ΔB0 variation, before being Fourier transformed again and concatenated.
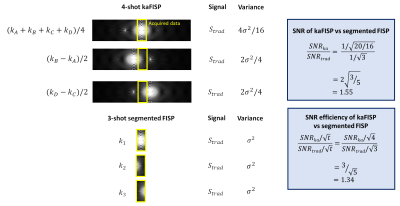
Figure 3: SNR and SNR efficiency comparisons between a 4-shot kaFISP acquisition, and the equivalent 3-shot segmented FISP acquisition at the nominal resolution. This assumes the weighting of the signals from F0 and F-1 states is approximately equal, which holds for T2>>TR when high flip angles (α≥40⁰) are used.
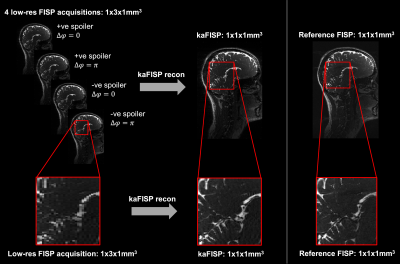
Figure 4: Whole head acquisitions in a healthy volunteer using both kaFISP (left) and a matched FISP (right) with the same readout bandwidth, TR, TE, flip angle, FOV and target resolution. The kaFISP comprises 4 fully sampled low-resolution acquisitions which, when combined, provide images at a resolution 3x higher than nominally acquired.
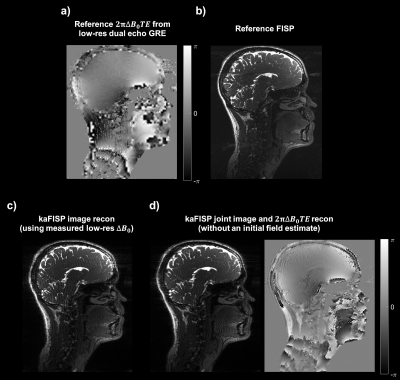
Figure 5: a) Low-resolution map of the phase term due to spatial ΔB0 variation (i.e. $$$2πΔB_0TE$$$) from the separately acquired dual-echo GRE data. b) Image obtained from the matched FISP reference scan with the same readout bandwidth, TR, TE, flip angle, FOV and target resolution. c) kaFISP image directly reconstructed using the phase term shown in a) in the forward model. d) Jointly reconstructed kaFISP image and phase offset term using the iterative scheme, with no initial ΔB0 estimate.