0502
MR Image Reconstruction via Zero-Shot Learned Generative Adversarial Transformers1Department of Electrical and Electronics Engineering, Bilkent University, Ankara, Turkey, 2National Magnetic Resonance Research Center (UMRAM), Bilkent University, Ankara, Turkey, 3Neuroscience Program, Aysel Sabuncu Brain Research Center, Bilkent University, Ankara, Turkey
Synopsis
Deep neural network models have demonstrated state-of-the-art performance in MR image reconstruction. These models require information regarding imaging operators during training, which limits their generalization. A recent framework is based on zero-shot learned generative models that learn MR image priors during training and couple imaging operator during inference on test acquisitions. Such models are however based on convolutional architectures that suffer from sub-optimal capture of long range dependencies. Here, we propose a novel architecture based on zero-shot learned generative adversarial transformers that enables efficient capture of long range dependencies via cross-attention transformers while removing reliance on imaging operator during training.
Introduction
Accelerated MRI involves a reconstruction procedure to map undersampled acquisitions to MR images that are as consistent as possible with fully-sampled acquisitions1. With their immense success in inverse problems, fully-supervised deep neural networks have recently been established as state-of-the-art in MRI reconstruction2-11. Supervised networks are trained based on explicit guidance from paired datasets of undersampled and fully-sampled acquisitions to learn an indirect prior that suppresses aliasing artifacts, and also from the imaging operator that reflects k-space sampling patterns and coil-sensitivity encoding. Yet, adoption of supervised models is challenging given difficulties in compiling large databases with paired acquisitions. Moreover, supervised models trained for a specific imaging operator typically show poor generalization to different undersampling rates or coil configurations. These limitations have sparked interest in approaches to relax supervision requirements. Targeting supervision related to raw data, a first group of studies have proposed models that can be trained on unpaired datasets12,13 or only undersampled acquisitions14. Note, however, that these models still require implicit supervision regarding the imaging operator, requiring retraining under notable changes to the operator to mitigate performance losses. A second approach instead targets supervision related to the imaging operator by decoupling the reconstruction process to two stages15,16: learning of the MRI prior, and reconstruction mapping by embedding of the imaging operator. Here, we introduce a novel MRI reconstruction inspired by this decoupling approach17. Unlike prior studies predominantly based on convolutional architectures, the proposed method uses a novel adversarial architecture with cross-attention transformers18 (SLATER) to capture long-range dependencies in the MRI prior. The learned prior is conjoined with the imaging operator during inference, and the reconstruction mapping is then performed directly on test data without any need for additional training samples. The proposed method eliminates the need for paired datasets for model training, and it improves generalization against practical variabilities in the imaging operator.Methods
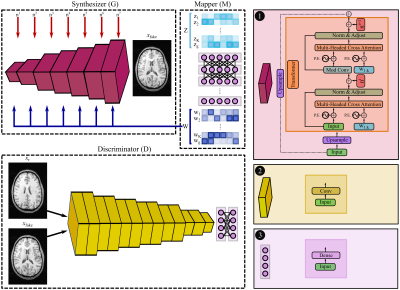
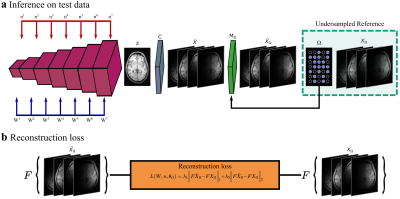
In the pre-training phase, SLATER first learns an MRI prior via generative modeling of coil-combined complex MR images. SLATER is an adversarial architecture with three sub-networks19 (Fig. 1): mapper ($$$M$$$), synthesizer ($$$G$$$), and discriminator ($$$D$$$). $$$M$$$ is a fully-connected network that maps i.i.d. Gaussian variables to intermediate global and local latent variables ($$$W$$$). $$$G$$$ is a hybrid architecture that synthesizes MR images via a cascade of cross-attention transformers and convolution layers. $$$G$$$ receives global latents to perform spatially-uniform modulation of image features, and local latents to perform spatially-selective modulations of image features in cross-attention transformers. $$$G$$$ also uses noise variables ($$$n$$$) to control fine structural details. $$$D$$$ aims to distinguish synthesized and actual MR images. Model training is performed to minimize an adversarial non-saturating logistic loss function using the Adam optimizer with a learning-rate of 0.001 for 1280 epochs.In the inference phase, the imaging operator is embedded to map candidate images synthesized by SLATER onto individual coils, and then to express consistency to acquired k-space coefficients based on the undersampling pattern (Fig. 2). Model adaptation is performed to update SLATER parameters to minimize this data-consistency loss:$$L(W,n,\theta_G)=\lambda_{1}\left\|F_{p}CG(W,n,\theta_G)-k\right\|_{1}+\lambda_{2}\left\|F_{p}CG(W,n,\theta_G)-k\right\|_{2}$$
$$$L$$$:data-consistency loss, $$$\theta_G$$$:synthesizer weights, ($$$\lambda_{1},\lambda_{2}$$$):weightings of ($$$\ell_1$$$,$$$\ell_2$$$) loss components, $$$C$$$:coil-sensitivity maps, $$$k$$$:acquired k-space coefficients, $$$F_p$$$:partial Fourier operator. Inference is performed using the RMSprop optimizer for 1000 iterations.
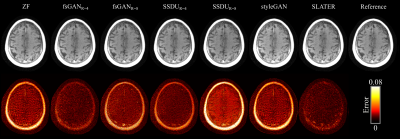
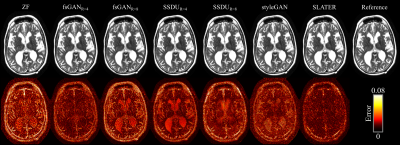
Demonstrations were performed on multi-coil T1- and T2-weighted acquisitions from fastMRI dataset20. (100,10,40) subjects were reserved for (training,validation,testing). SLATER was compared against: 1) A fully-supervised GAN model (fsGAN) trained using paired undersampled and fully-sampled acquisitions. 2) A self-supervised model (SSDU)14 trained using undersampled acquisitions. 3) A decoupled reconstruction model (styleGAN)19, similar to SLATER, but entirely based on a convolutional architecture. Note that fsGAN and SSDU use information regarding the imaging operator during training, whereas SLATER and styleGAN do not. All acquisitions were retrospectively undersampled via 2D random undersampling at R=4 and 8 using Gaussian sampling density.
Results
Table 1 lists PSNR and SSIM across reconstructed test images at acceleration rate R=4. When the acceleration rate is fixed during training and testing (R=4), SLATER performs on par with fsGAN, outperforms SSDU by 1.9dB PSNR, 0.3% SSIM, and styleGAN by 3.8dB PSNR, 2.7% SSIM. Performance improvements with SLATER are clearly depicted in representative reconstructions in Figs. 3-4.We also examined the reliability of SLATER against variability in the imaging operator: R=8 was assumed during training, while R=4 was used during testing. As predicted, fsGAN and SSDU that are trained with supervision regarding the imaging operator show an average performance loss of 2.4dB PSNR, 1.9% SSIM (Table 1). In contrast, decoupled methods including SLATER do not suffer any performance loss as their training is agnostic to the imaging operator. These observations are also manifested in representative reconstructions in Figs. 3-4.
Conclusion
Here we introduced a novel MRI reconstruction technique based on an adversarial transformer architecture, SLATER. SLATER pre-trains a high-quality MRI prior in a generative modeling task, and then adapts its prior for the reconstruction task by embedding the imaging operator during inference. This decoupled approach allows improved generalization performance under deviations in the imaging operator compared to prior supervised and self-supervised models. Furthermore, the contextual sensitivity of cross-attention transformers in SLATER enables capture of a higher-quality MRI prior compared to pure convolutional architectures. Therefore, the proposed method holds great promise for improving utility of accelerated MRI reconstructions.Acknowledgements
This work was supported in part by a TUBA GEBIP fellowship, by a TUBITAK 1001 Grant (118E256), and by a BAGEP fellowship awarded to T. Çukur.References
[1] M. Lustig, D. Donoho, and J. M. Pauly, “Sparse MRI: The application of compressed sensing for rapid MR imaging,” Magn. Reson. Med., vol. 58, no. 6, pp. 1182–1195, 2007.
[2] H. K. Aggarwal, M. P. Mani, and M. Jacob, “MoDL: Model-Based Deep Learning Architecture for Inverse Problems,” IEEE Trans. Med. Imaging, vol. 38, no. 2, pp. 394–405, 2019.
[3] S. U. H. Dar, M. Özbey, A. B. Çatlı, and T. Çukur, “A Transfer-Learning Approach for Accelerated MRI Using Deep Neural Networks,” Magn. Reson. Med., vol. 84, no. 2, pp. 663–685, 2020.
[4] K. Hammernik, T. Klatzer, E. Kobler, M. P. Recht, D. K. Sodickson, T. Pock, and F. Knoll, “Learning a variational network for reconstruction of accelerated MRI data,” Magn. Reson. Med., vol. 79, no. 6, pp. 3055–3071, Jun. 2018.
[5] Y. Han, J. Yoo, H. H. Kim, H. J. Shin, K. Sung, and J. C. Ye, “Deep learning with domain adaptation for accelerated projection-reconstruction MR,” Magn. Reson. Med., vol. 80, no. 3, pp. 1189–1205, 2018.
[6] M. Mardani, E. Gong, J. Y. Cheng, S. S. Vasanawala, G. Zaharchuk, L. Xing, and J. M. Pauly, “Deep Generative Adversarial Neural Networks for Compressive Sensing (GANCS) MRI,” IEEE Trans. Med. Imaging, vol. 38, no. 1, pp. 167–179, Jan. 2019.
[7] J. Schlemper, J. Caballero, J. V. Hajnal, A. Price, and D. Rueckert, “A Deep Cascade of Convolutional Neural Networks for MR Image Reconstruction,” in International Conference on Information Processing in Medical Imaging, 2017, pp. 647–658.
[8] S. Wang, Z. Su, L. Ying, X. Peng, S. Zhu, F. Liang, D. Feng, and D. Liang, “Accelerating magnetic resonance imaging via deep learning,” in IEEE 13th International Symposium on Biomedical Imaging (ISBI), 2016, pp. 514–517.
[9] Y. Yang, J. Sun, H. Li, and Z. Xu, “Deep ADMM-Net for Compressive Sensing MRI,” in Advances in Neural Information Processing Systems, 2016.
[10] S. Yu, H. Dong, G. Yang, G. Slabaugh, P. L. Dragotti, X. Ye, F. Liu, S. Arridge, J. Keegan, D. Firmin, and Y. Guo, “DAGAN: Deep de-aliasing generative adversarial networks for fast compressed sensing MRI reconstruction,” IEEE Trans. Med. Imaging, vol. 37, no. 6, pp. 1310–1321, 2018.
[11] B. Zhu, J. Z. Liu, B. R. Rosen, and M. S. Rosen, “Image reconstruction by domain transform manifold learning,” Nature, vol. 555, no. 7697, pp. 487–492, 2018.
[12] G. Oh, B. Sim, H. Chung, L. Sunwoo, and J. C. Ye, “Unpaired Deep Learning for Accelerated MRI Using Optimal Transport Driven CycleGAN,” IEEE Trans. Comput. Imaging, vol. 6, pp. 1285–1296, 2020.
[13] K. Lei, M. Mardani, J. M. Pauly, and S. S. Vasanawala, “Wasserstein GANs for MR Imaging: From Paired to Unpaired Training,” IEEE Trans. Med. Imaging, vol. 40, no. 1, pp. 105–115, 2021.
[14] B. Yaman, S. A. H. Hosseini, S. Moeller, J. Ellermann, K. Uğurbil, and M. Akçakaya, “Self-supervised learning of physics-guided reconstruction neural networks without fully sampled reference data,” Magn. Reson. Med., vol. 84, no. 6, pp. 3172–3191, 2020.
[15] D. Narnhofer, K. Hammernik, F. Knoll, and T. Pock, “Inverse GANs for accelerated MRI reconstruction,” in Wavelets and Sparsity XVIII, 2019, vol. 11138, pp. 381–392.
[16] K. C. Tezcan, C. F. Baumgartner, R. Luechinger, K. P. Pruessmann, and E. Konukoglu, “MR Image Reconstruction Using Deep Density Priors,” IEEE Trans. Med. Imaging, vol. 38, no. 7, pp. 1633–1642, 2019.
[17] Y. Korkmaz, S. U. H. Dar, M. Yurt, M. Özbey, and T. Çukur, “Unsupervised MRI Reconstruction via Zero-Shot Learned Adversarial Transformers,” arXiv Prepr. arXiv:2105.08059, 2021.
[18] D. A. Hudson and C. L. Zitnick, “Generative Adversarial Transformers,” arXiv Prepr. arXiv2103.01209, 2021.
[19] T. Karras, S. Laine, M. Aittala, J. Hellsten, J. Lehtinen, and T. Aila, “Analyzing and Improving the Image Quality of StyleGAN,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020, pp. 8110–8119.
[20] F. Knoll, J. Zbontar, A. Sriram, M. J. Muckley, M. Bruno, A. Defazio, M. Parente, K. J. Geras, J. Katsnelson, H. Chandarana, Z. Zhang, M. Drozdzalv, A. Romero, M. Rabbat, P. Vincent, J. Pinkerton, D. Wang, N. Yakubova, E. Owens, C. L. Zitnick, M. P. Recht, D. K. Sodickson, and Y. W. Lui, “fastMRI: A Publicly Available Raw k-Space and DICOM Dataset of Knee Images for Accelerated MR Image Reconstruction Using Machine Learning,” Radiol. Artif. Intell., vol. 2, no. 1, p. e190007, 2020.
Figures