0501
EigenMRI: Data-driven shallow-learning reconstruction of undersampled MRI data
Ricardo Otazo1,2, Ramin Jafari1, and Masoud Zarepisheh1
1Department of Medical Physics, Memorial Sloan Kettering Cancer Center, New York, NY, United States, 2Department of Radiology, Memorial Sloan Kettering Cancer Center, New York, NY, United States
1Department of Medical Physics, Memorial Sloan Kettering Cancer Center, New York, NY, United States, 2Department of Radiology, Memorial Sloan Kettering Cancer Center, New York, NY, United States
Synopsis
Machine learning, and specifically deep learning, has recently demonstrated high-performance reconstruction of undersampled k-space data. However, training of deep learning reconstruction methods does not take advantage of the thousands of previously acquired images that are stored in clinical databases. Inspired by the eigenfaces method from computer vision, where an image model derived from thousands of pre-existing images is used to identify new faces, this work presents an image reconstruction method named EigenMRI that learns a data-driven regularization approach using thousands of images extracted from a clinical database to reconstruct 3D brain images with 2D acceleration
Introduction
Machine learning, and specifically deep learning, has recently demonstrated high-performance reconstruction of undersampled k-space data [1-2]. However, training of deep learning reconstruction methods usually requires the acquisition of new datasets and does not take advantage of the thousands of previously acquired images that are stored in clinical databases. Inspired by the eigenfaces method from computer vision [3-4], where an image model derived from thousands of pre-existing images is used to identify new faces, this work presents an image reconstruction method named EigenMRI that learns a data-driven regularization approach using thousands of images extracted from a clinical database to reconstruct 3D brain images with 2D acceleration.Methods
EigenMRI reconstruction: EigenMRI exploits correlations between thousands of images acquired with the same pulse sequence to form a space with lower dimensionality than the original MRI space (Figure 1). Defining U as a linear mapping between the eigenMRI space and the original MRI space, minimization of the difference between the image to be reconstructed (m) and its projection onto the eigenMRI space (UU*m) will promote a solution in the eigenMRI space that would require fewer k-space samples. EigenMRI reconstruction is formulated as the following convex optimization problem:$$\min_{m}||Em-d||_2^2+\lambda||UU^*m-m||_1,$$ where E is the data acquisition operator including FFT, undersampling pattern and coil sensitivities and d is the undersampled k-space data. The left term promotes data consistency, and the right term is the eigenMRI regularization. The L1-norm is used in the regularization part since the difference is expected to be sparse. λ weights the eigenMRI regularization relative to data consistency.
Computation of the eigenMRI space (U): Each training image was sorted as a column of a data matrix D (number or rows = image size, number of columns = number of training images) (Figure 2.a). D is an extremely low-rank matrix due to high correlations between training images, and therefore U was computed as the principal left singular vectors of the matrix D.
EigenMRI reconstruction of undersampled 3D brain data: The proposed eigenMRI technique was demonstrated on 3D T1-weighted brain MRI acquisitions. Since 2D acceleration is performed along ky and kz (coronal plane), 25,312 coronal images from 112 brain tumor datasets were used to compute the eigenMRI space U. The 112 brain tumor datasets were extracted from our clinical database (PACS) using an IRB-approved retrospective data collection protocol. Three patients with brain tumors were scanned with the same 3D T1-weighted technique on a 3T scanner (MR750W, GE Healthcare) using a 12-channel coil array. 3D k-space was fully-sampled to obtain a reference to benchmark different reconstruction techniques. Acquisition matrix size was 256x256x184 and each dataset was retrospectively undersampled by a factor of 2x2 in the ky-kz plane using a uniform undersampling pattern and fully-sampled 24x24 central k-space region. EigenMRI reconstruction was implemented in Matlab (The Mathworks) using a conjugate gradient algorithm to solve Eq. (1) for each undersampled coronal slice. Multicoil compressed sensing reconstruction using a 3D wavelet transform (CS-Wavelets) [5] was performed for comparison purposes.
Results
The rank of the training data matrix D was 969 (1% cutoff), which was much lower than the original dimensionality in the coronal plane 184x256=47,104. Therefore, the first 1,000 columns of U were employed to define the eigenMRI space (Figure 2.b). Figure 2.c shows the first 10 eigen MRI slices that define the eigenMRI space. Figure 3 shows reconstruction of 3D MRI data acquired with 2x2 acceleration on a patient with glioblastoma. The proposed eigenMRI presents higher performance that CS-Wavelets, including reduced residual undersampling artifacts and increased image sharpness. The red arrows show residual aliasing artifacts in CS-Wavelets. Normalized root mean squared error with respect to the fully-sampled reference was 0.172 (eigenMRI) and 0.221 (CS-Wavelets) for the whole volume and 0.098 (eigenMRI) and 0.156 (CS-Wavelets) for the tumor region. Figure 4 shows reconstruction results in another brain tumor patient. EigenMRI presents higher performance than CS-Wavelets, in concordance with the previous patient in Figure 3.Discussion
The proposed EigenMRI reconstruction technique performs a data-driven regularization for reconstruction of undersampled MRI data. Images acquired with similar anatomical coverage and contrast were used as prior information to constrain the reconstruction problem, which compares favorably to compressed sensing techniques, where the image model is analytical and usually simple. Higher accelerations than 2x2 might be feasible by including more datasets to form the eigenMRI space. The proposed eigenMRI technique represents a shallow learning technique which does not require the use of deep convolutional networks to learn the regularization approach.Conclusion
This work demonstrates the utilization of previously acquired images to learn a data-driven regularization technique for reconstruction of undersampled MRI data. The proposed eigenMRI technique presents improved performance than compressed sensing using wavelets in the reconstruction of 3D brain tumor MRI data with 2x2 acceleration. EigenMRI is one of the first techniques to take advantage of the thousands of images stored in clinical databases for the purpose of reconstruction of undersampled MRI data.Acknowledgements
No acknowledgement found.References
- Zhu B et al. Image reconstruction by domain-transform manifold learning. Nature 2018; 555(7697):487.
- Hammernik K et al. Learning a variational network for reconstruction of accelerated MRI data. Magn Reson Med 2018; 79(6):3055–71.
- Sirovich L, Kirby M. Low-dimensional procedure for the characterization of human faces. J Opt Soc Am A 1987;4(3):519-24.
- Turk M, Pentland A. Face recognition using eigenfaces. Proc. IEEE Conference on Computer Vision and Pattern Recognition 1991, pp. 586–591.
- Chandarana H et al. Three-dimensional MR Cholangiopancreatography in a Breath Hold with Sparsity-based Reconstruction of Highly Undersampled Data. Radiology. 2016;280(2):585-94.
Figures
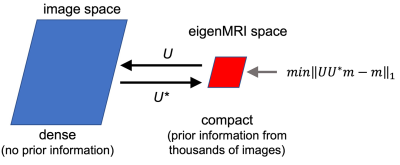
Figure 1: General idea of the eigenMRI reconstruction method. The eigenMRI space (defined by U) is formed by exploiting correlations among thousands of images acquired with the same pulse sequence, and therefore it has lower dimensionality than the original image space. Minimizing the difference between the image to be reconstructed (m) and its projection onto the eigenMRI space (UU*m) will promote a solution in the eigenMRI space that would require fewer k-space samples.

Figure 2: a) Computation of the eigenMRI space: each training image was sorted as a column of a matrix D and singular value decomposition was employed to obtain the matrix U. Since 2D acceleration in the ky-kz plane (coronal orientation) of 3D acquisitions was performed, 25,312 coronal images from 112 brain tumor datasets were used for training. b) The rank of D was 969 (1% cutoff), which was much lower than the original dimensionality in the coronal plane 184x256=47,104. The first 1,000 columns of U were employed to define the eigenMRI space. c) First 10 eigenMRI basis functions.
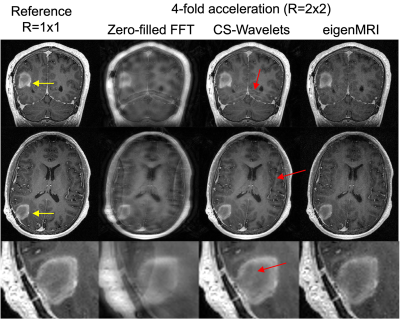
Figure 3: Reconstruction of a 3D T1-weighted acquisition with 2x2 acceleration in a different patient with glioblastoma using zero-filled FFT, compressed sensing with 3D wavelets (CS-Wavelets) and the proposed eigenMRI. The fully-sampled reference is included for comparison. Representative coronal and axial slices with the brain tumor (yellow arrow) are included. EigenMRI presents improved removal of undersampling artifacts (red arrows show residual aliasing artifacts in CS-Wavelets) and increased image sharpness in the tumor region relative to CS-Wavelets.
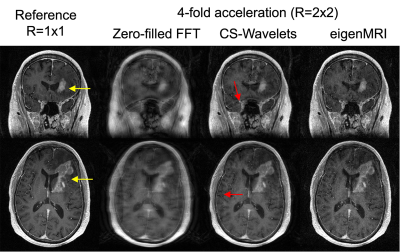
Figure 4: Reconstruction of a 3D T1-weighted acquisition with 2x2 acceleration in a different patient with a different brain tumor using zero-filled FFT, CS-Wavelets and the proposed eigenMRI. Representative coronal and axial slices with the brain tumor (yellow arrow) are included. In concordance with the example in Figure 3, EigenMRI presents higher performance than CS-Wavelets (red arrows show residual aliasing artifacts in CS-Wavelets).
DOI: https://doi.org/10.58530/2022/0501