Introduction

Deep neural networks were shown to improve reconstruction quality of undersampled k-space data. Physics-based neural networks^1,2 reduce the amount of required training data but still require a fully sampled ground truth reference for training, which is not available for cardiac real-time data.
Recently, self-supervised reconstruction networks have been proposed which are trained without any ground truth reference by splitting the acquired k-space data in two sets and learn a reconstruction of the first set which is consistent with the second. Self-supervised networks are reported to achieve similar reconstruction quality compared to networks trained with a ground truth reference.³
In this work, we exploit the self-supervised training strategy to train NLINV-Net for reconstructing cardiac real-time data. NLINV-Net is inspired by NLINV⁴ and jointly estimates image and coil sensitivity maps (CSMs). The motivation to use NLINV-Net in this work is threefold:
1. Joint estimation of image and CSMs can improve classical⁴ and learned⁵ reconstruction methods.
2. NLINV has been successfully applied to cardiac real-time reconstruction⁶.
3. As no calibration step is required, NLINV-Net takes raw k-space data as input, making it a natural choice for the training strategy described in [3].

Theory and Methods

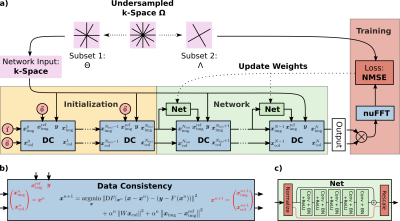
NLINV⁴ jointly estimates the image and CSMs by solving the non-linear inverse problem
$$\begin{aligned}\begin{pmatrix}\boldsymbol{x}_{\mathrm{img}}\\\boldsymbol{x}_{\mathrm{col}}\end{pmatrix}=\boldsymbol{x}=\underset{\boldsymbol{x}}{\operatorname{argmin}} \lVert F(\boldsymbol{x})-\boldsymbol{y}\rVert_2^2\,.&&&(1)\end{aligned}$$Here, $$$F$$$ is the non-linear SENSE forward operator (c.f. Fig. 1) taking the image $$$\boldsymbol{x}_{\mathrm{img}}$$$ and the CSMs $$$\boldsymbol{x}_{\mathrm{col}}$$$ as inputs and mapping them to the k-space data $$$\boldsymbol{y}$$$. The non-linear problem is solved using the iteratively regularized Gauss-Newton method (IRGNM). In each Gauss-Newton step, the iterate $$$\boldsymbol{x}^{n}$$$ is updated by solving the linearized subproblem, i.e.
$$\begin{aligned}\boldsymbol{x}^{n+1}=\underset{\boldsymbol{x}}{\operatorname{argmin}}\lVert \mathrm{D}F|_{\boldsymbol{x}^n}\left(\boldsymbol{x}-\boldsymbol{x}^n\right)-\left(\boldsymbol{y}-F\left(\boldsymbol{x}^n\right)\right)\rVert_2^2+\alpha_n\lVert\boldsymbol{x}_{\mathrm{img}}\rVert_2^2+\alpha_n\lVert W\boldsymbol{x}_{\mathrm{col}}\rVert_2^2\,.&&&(2)\end{aligned}$$ Here, $$$\mathrm{D}F|_{\boldsymbol{x}^n}$$$ is the Fréchet derivative of $$$F$$$ evaluated at $$$\boldsymbol{x}^n$$$, $$$\alpha_n$$$ is a regularization parameter reduced by a factor of two in each iteration and $$$W$$$ is a weighting matrix such that $$$\boldsymbol{x}_{\mathrm{col}}$$$ is penalized by a Sobolev norm to promote smooth CSMs.

NLINV-Net unrolls the IRGNM and includes a neural network based regularization term for $$$\boldsymbol{x}_{\mathrm{img}}$$$. The modified update rule, including a trainable regularization parameter $$$\lambda\ge 0$$$, reads $$\begin{aligned}\boldsymbol{x}^{n+1}=\underset{\boldsymbol{x}}{\operatorname{argmin}}\lVert\mathrm{D}F|_{\boldsymbol{x}^n}\left(\boldsymbol{x}-\boldsymbol{x}^n\right)-\left(\boldsymbol{y}-F\left(\boldsymbol{x}^n\right)\right)\rVert_2^2+(\alpha_n+\lambda)\lVert\boldsymbol{x}_{\mathrm{img}}-\mathrm{Net}(\boldsymbol{x}^n_{\mathrm{img}})\rVert_2^2+\alpha_n\lVert W\boldsymbol{x}_{\mathrm{col}}\rVert_2^2\,.&&&(3)\end{aligned}$$$$$\mathrm{Net}$$$ is a residual network (c.f. Fig. 2c) with 64-channel complex-valued convolutions, batch normalization and ReLU activations. Its input is normalized to a maximum magnitude of one, and the output is rescaled to the original value. The network weights are shared across iterations. The data-consistency module solving Eq. 3 (c.f. Fig. 2b) and its derivatives are implemented using the conjugate gradient algorithm. We unroll the IRGNM for $$$N=12$$$ iterations but use no network regularization (i.e. plain NLINV) in the first $$$N_{\mathrm{ini}}=N-N_{\mathrm{net}}$$$ iterations for initialization (c.f. Fig. 2a).

Self-Supervised Training Strategy
We trained NLINV-Net utilizing a real-time dataset acquired with a balanced SSFP radial FLASH sequence (TR=2.56ms, TE=1.28ms, FA=23°, FOV=256x256mm) on a Siemens Skyra 3T scanner (Siemens Healthcare GmbH, Erlangen, Germany). Multiple slices were acquired from 25 volunteers, resulting in 66.960 frames with 39 spokes each. The k-space was coil combined to $$$N_C=10$$$ virtual coils and gradient delays were estimated utilizing RING⁷.
Following [3], we split the acquired k-space data $$$\Omega$$$ into two disjunct subsets $$$\Theta$$$ and $$$\Lambda$$$. We experimented with two different splitting strategies, i.e. splitting the k-space spoke-wise or point-wise. Each spoke or point was selected with a probability $$$p$$$ to be contained in the first set $$$\Theta$$$, the remaining data were assigned to $$$\Lambda$$$. $$$\Theta$$$ is used by NLINV-Net to estimate the image $$$\boldsymbol{x}_{\mathrm{img}}$$$ and CSMs $$$\boldsymbol{x}_{\mathrm{col}}$$$. From that, the k-space of $$$\Lambda$$$ is predicted by the non-linear forward model with the respective pattern. The weights of NLINV-Net are optimized to minimize the normalized mean squared error of the predicted and actual k-space data in $$$\Lambda$$$ (c.f. Fig. 2.a).
We initialize the weights by training for one epoch with $$$N_{\mathrm{net}}=1$$$ network iteration. Afterwards, NLINV-Net with $$$N_{\mathrm{net}}=3$$$ or $$$N_{\mathrm{net}}=5$$$ iterations is trained for another epoch. NLINV-Net was implemented based on the new neural network framework in BART^8,9. Training takes about 7, 10 and 14 hours for the $$$N_{\mathrm{net}}=1,\;3\;\text{and}\;5$$$ iterations network on an Nvida A100 GPU.

Results

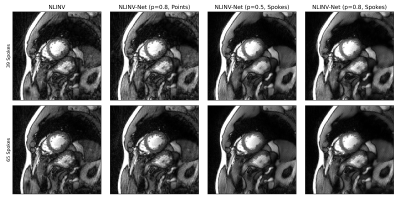
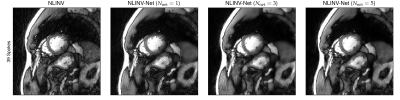
We present example reconstructions using NLINV-Net with $$$N_{\mathrm{net}}=3$$$ network iterations and different training splittings in Fig. 3. As a baseline reconstruction, we provide reconstructions using plain NLINV. Since no ground truth reference is available, only a qualitative comparison of the reconstruction is possible. We observe that NLINV-Net with spoke-wise splitting reduces streaking artifact significantly compared to plain NLINV. In contrast, NLINV-Net trained with point-wise splitting is very similar to plain NLINV.
In Fig. 4, we compare reconstructions with NLINV-Net using different numbers of network iterations $$$N_{\mathrm{net}}$$$. Using $$$N_{\mathrm{net}}=3$$$ iterations slightly improves reconstruction quality compared to $$$N_{\mathrm{net}}=1$$$. The difference for $$$N_{\mathrm{net}}=3$$$ and $$$N_{\mathrm{net}}=5$$$ is minor.

Discussion and Conclusion

This work presents a NLINV-Net, a network architecture for non-linear physics-based reconstruction, and a self-supervised training strategy to train NLINV-Net without any ground truth reference data on a real-time cardiac dataset. A spoke-wise splitting strategy of the acquired k-space data seems to be superior compared to a point-wise strategy. We expect further improvement of NLINV-Net by combining NLINV-Net with - possibly learned - temporal regularization.

References

1. K. Hammernik et al., “Learning a variational network for reconstruction of accelerated MRI data”, Magnetic Resonance in Medicine, vol. 79, no. 6, pp. 3055–3071, 2018

2. H. K. Aggarwal, M. P. Mani, and M. Jacob, “MoDL: Model-Based Deep Learning Architecture for Inverse Problems”, IEEE Transactions on Medical Imaging, vol. 38, no. 2, pp. 394–405, 2019

3. B. Yaman, S. A. H. Hosseini, S. Moeller, J. Ellermann, K. Uğurbil, and M. Akçakaya, “Self-supervised learning of physics-guided reconstruction neural networks without fully sampled reference data,” Magn. Reson. Med., vol. 84, no. 6, 2020

4. M. Uecker, T. Hohage, K. T. Block, and J. Frahm, “Image reconstruction by regularized nonlinear inversion-joint estimation of coil sensitivities and image content,” Magn. Reson. Med., vol. 60, no. 3, pp. 674-682, 2008

5. M. Arvinte, S. Vishwanath, A. H. Tewfik, and J. I. Tamir, "Deep J-Sense: An unrolled network for jointly estimating the image and sensitivity maps", ISMRM Annual Meeting 2021, In Proc. Intl. Soc. Mag. Reson. Med. 29;1755, 2021

6. M. Uecker, S. Zhang, D. Voit, A. Karaus, K.-D. Merboldt, and J. Frahm, “Real-time MRI at a resolution of 20 ms,” NMR Biomed., vol. 23, no. 8, 2010, doi: 10.1002/nbm.1585.

7. S. Rosenzweig, H. C. M. Holme, and M. Uecker, “Simple auto-calibrated gradient delay estimation from few spokes using Radial Intersections (RING),” Magn. Reson. Med., vol. 81, no. 3, 2019

8. M. Uecker et al., "BART Toolbox for Computational Magnetic Resonance Imaging", Zenodo, DOI: 10.5281/zenodo.592960

9. M. Blumenthal and M. Uecker, "Deep, Deep Learning with BART", ISMRM Annual Meeting 2021, In Proc. Intl. Soc. Mag. Reson. Med. 29;1754, 2021