Introduction

Ultra-high-field MRI is prone to severe signal and contrast loss that can be addressed using parallel transmission. In 2D multi-slice acquisitions, the $$$B_1^+$$$ inhomogeneity is generally solved on a slice-by-slice RF shimming¹ or multi-spoke pulses². For both approaches, pTX largely outperforms sTx as it offers additional degrees of freedoms to control the spatial $$$B_1^+$$$ and flip angle (FA) distributions. Up to now, subject tailored 2D slice-selective pulses² as well as pre-computed slice-selective universal pulses have been proposed³. These solutions are valid for a given set of predefined protocols, in particular slice positions and orientations. If the user needs to tilt or shift the slices, one must re-compute the whole set of pulses. Here, we introduce a new concept called "meta-pulses" which expresses the spokes coefficients and gradient blips as smooth functions of the slice position and orientation. This solution can be used to generate tailored as well as universal pulses, i.e. pulses designed off-line on a database of RF and static field offset maps.

Theory

A slice selective multi-spoke multi-channel pulse ($$$N_s$$$ spokes, $$$N_c$$$ channels) can be defined as (A,B) where A is a matrix of complex RF coefficients ($$$N_c\times{N_s}$$$) and B defines the spoke locations with real coefficients ($$$3\times{N_s}$$$). We propose to define the coefficients $$$a_{i,j},b_{i,j}$$$ of the A and B matrices as functions of the slice orientation defined by its normal vector $$$\mathbf{n}$$$ and the slice position $$$z$$$ relative to magnet isocenter with $$$a_{i,j}=f_{i,j}(\mathbf{n},z)$$$ and $$$b_{i,j}=g_{i,j}(\mathbf{n},z)$$$. To promote smoothness of the resulting FA distribution along $$$\mathbf{n}$$$, we then need to choose adequately $$$f$$$ and $$$g$$$ such that they represent continuous functions. A possible approach is to express them as finite series of complex spherical harmonics $$$Y_l^m(\mathbf{n})$$$: $$f_{i,j}(\mathbf{n},z)=\sum_{k=0}^{p}z^k.( \sum_{l,m}^{}f_{i,j,k,l,m}.Y_l^m(\mathbf{n}))$$ That way, each function $$$f_{i,j}$$$ is represented as a finite set of coefficients $$$(f_{i,j,k,l,m})$$$. Similarly, using real spherical harmonics, $$$g_{i,j}$$$ can be defined using a set of real coefficients $$$g_{i,j,k’,l’,m’}$$$. By denoting $$$\mathbf{X}$$$ the whole set of $$$f_{i,j,k,l,m}$$$ and $$$g_{i,j,k’,l’,m’}$$$ coefficients, we can associate to $$$\mathbf{X}$$$ the 2D-selective pulse $$$(A(\mathbf{X},z, \mathbf{n}),B(\mathbf{X},z, \mathbf{n}))$$$ and compute the FA obtained at any position $$$\mathbf{r}$$$ where $$$z=\mathbf{r}\cdot{\mathbf{n}}$$$. For the optimization of the spherical harmonics coefficients arranged in the vector $$$\mathbf{X}$$$, we define the error metric $$$\epsilon(\mathbf{X})$$$ as the mean quadratic error relative to the target FA $$$\alpha_{T}$$$ within a region of interest $$$R$$$ integrated over all possible slice configurations $$$\mathbf{r}$$$ and $$$\mathbf{n}$$$: $$\epsilon(\mathbf{X})=\sum_{\mathbf{r} \in R}(\frac{1}{4\pi\alpha_{T}^{2}}\iint_\mathbf{n}(\alpha_{\mathbf{n},\mathbf{r}}(\mathbf{X})-\alpha_{T} )^2d^2\mathbf{n})$$ where $$$\alpha_{\mathbf{n},\mathbf{r}}(\mathbf{X})$$$ is the FA at position $$$\mathbf{r}$$$ for the slice-selective pulse $$$(A(\mathbf{X},z,\mathbf{n}),B(\mathbf{X},z,\mathbf{n}))$$$. Minimizing $$$\epsilon(\mathbf{X})$$$ under SAR and/or power constraints leads to an optimized solution of computable multi-slice multi-spoke pulses defined by their set of coefficients: a "meta-pulse".

Methods

In this demonstration, we will limit our concept to a slice that can tilt in one orientation from axial to coronal. The normal vector $$$\mathbf{n}$$$ then becomes the variable $$$\theta, (\phi=0)$$$. We choose $$$f$$$ and $$$g$$$ as follows: $$f_{i,j}(\theta,z)=\sum_{k=0}^{p}z^k.(\sum_{l=-q}^{q} f_{i,j,k,l}.e^{ \mathbf{i}l\theta})$$ $$g_{i,j}(\theta,z)=\sum_{k=0}^{p’}z^k.(\sum_{l=0}^{q’} g_{i,j,k,l}.cos(l \theta)+\sum_{l=1}^{q’} g_{i,j,k,-l}.sin(l \theta))$$ In this demonstration, we used $$$p=p’=6$$$ and $$$q=q’=4$$$. Meta-pulses, referred as universal, were designed offline with 1-spoke and 2-spokes using a database of in vivo $$$B_0/B_1^+$$$ maps acquired prior to this study³. Acquisitions were performed on a healthy volunteer on an investigational Magnetom 7T scanner (Siemens Healthineers, Germany) equipped with a 8Tx/32Rx pTx coil (Nova Medical, USA). $$$B_0/B_1^+$$$ maps were acquired with respectively $$$2.5$$$mm and $$$5$$$mm isotropic resolutions to compute tailored pulses. A standard slice-by-slice approach was used for 1-spoke and 2-spokes solutions. Additionally, a 1-spoke tailored meta-pulse was computed. A $$$T2^*_w$$$ 2D gradient-recalled-echo acquisition (0.5mm in-plane, FA=50°, TR=1800ms, TE=20ms, 56 slices of thickness 2 mm) was repeated in radiological CA-CP orientation (~7° slice tilting) using a CP-mode and the 5 different pulse designs. A coronal orientation scan was also performed with meta-pulses which did not require additional pulse design. When meta-pulses were used, the 8-channel RF pulses were instantaneously computed online (evaluations inside the sequence’s executable) using the analytical functions described above by using the slice positions and orientations chosen by the MR operator.

Results

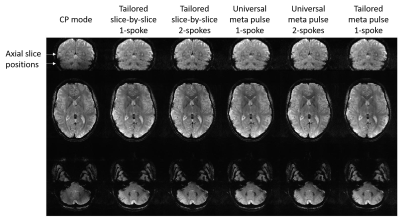
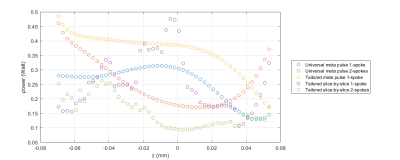
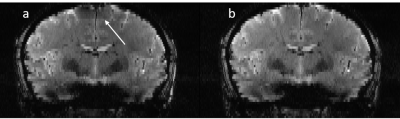
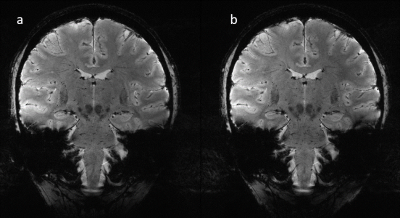
Fig.1 shows the superior performance of the different approaches compared to the $$$T2^*_w$$$ images acquired in CP mode. In Fig.2, as expected the simulated FA maps depict a better homogeneity of the tailored approaches compared to universal meta-pulses. The energy deposition shown in figure 3 reflects the continuity of the meta-pulse solutions along the 50 slices of the $$$T2^*_w$$$ protocol compared to the slice-by-slice solutions, which promotes signal smoothness. Consequently, the signal discontinuity observed through slices (Fig.4) is inherently solved by the meta-pulse design. A coronal acquisition using meta-pulses is shown in Fig.5.

Discussion/Conclusion

By using meta-pulses, it becomes possible to acquire 2D slice-selective protocols using pTx with optimized pulses without being restricted to a predefined number of slices, slice positions and orientations. This concept can use a tailored approach or calibration-free universal pulses. The meta-pulse parametrization being general, a slight penalty in excitation homogeneity yet is a price to pay to obtain an important flexibility to bring pTx to clinical routine. In conclusion, MetaPulse2D is a promising solution to enable universal slice-specific RF shimming or spokes pulses and may be used in various multi-slice 2D imaging such as turbo spin-echo, fMRI and dMRI.

Acknowledgements

This work has been supported by the Leducq Foundation large equipment ERPT program and has received funding from the European Union Horizon 2020 Research and Innovation program under Grant Agreements No. 885876 (AROMA).