0433
Uncertainty-Aware Physics-Driven Deep Learning Network for Fat and R2* Quantification in Self-Gated Free-Breathing Stack-of-Radial MRI1Department of Radiological Sciences, University of California Los Angeles, Los Angeles, CA, United States, 2Department of Bioengineering, University of California Los Angeles, Los Angeles, CA, United States, 3Department of Pediatrics, University of California Los Angeles, Los Angeles, CA, United States
Synopsis
MRI noninvasively quantifies liver fat and iron in terms of proton-density fat fraction (PDFF) and R2*. While conventional Cartesian-based methods require breath-holding, recent self-gated free-breathing radial techniques have shown accurate and repeatable PDFF and R2* mapping. However, data oversampling or computationally expensive reconstruction is required to reduce radial undersampling artifacts due to self-gating. This work developed an uncertainty-aware physics-driven deep learning network (UP-Net) that accurately and rapidly quantifies PDFF and R2* using data from self-gated free-breathing stack-of-radial MRI. UP-Net used an MRI physics loss term to guide quantitative mapping, and also provided uncertainty estimation for each quantitative parameter.
Introduction
MRI noninvasively quantifies liver fat and iron in terms of proton-density fat fraction (PDFF)1 and R2*2. While conventional Cartesian-based methods require breath-holding (BH), recent self-gated stack-of-radial techniques have demonstrated accurate and repeatable free-breathing (FB) PDFF/R2* quantification3,4. To reduce radial undersampling streaking artifacts after self-gating, data oversampling3 and compressed-sensing (CS) reconstruction5 have been proposed but had longer acquisition or computational time.Deep learning (DL)-based methods can rapidly reconstruct images from undersampled data6,7. DL has also been applied in Cartesian-based PDFF and/or R2* mapping to replace the time-consuming signal fitting process8-10. To characterize confidence in DL-based quantitative maps, DL with uncertainty estimation is a promising strategy11,12.
In this work, we developed a new uncertainty-aware physics-driven deep learning network (UP-Net) that accurately quantifies PDFF and R2* from self-gated free-breathing stack-of-radial MRI, without the need for data oversampling and with rapid inference time. We trained UP-Net with an MRI physics loss term to guide quantitative mapping. In addition, we incorporated uncertainty estimation in UP-Net for each quantitative parameter and characterized its relationship with quantification errors.
Methods
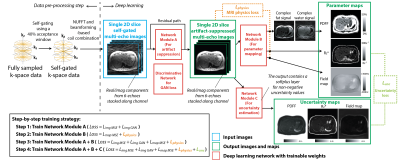
UP-Net Framework: UP-Net consists of 3 modules for artifact suppression, parameter mapping, and uncertainty estimation (Figure 1), each implemented using 2D U-Net13. UP-Net inputs were self-gated multi-echo 2D images from the 3D stack-of-radial dataset. The outputs were: (1) artifact-suppressed images $$$\hat{m}$$$, (2) quantitative maps $$$\hat{p}$$$ (fat&water signal/R2*/B0 field map), and (3) uncertainty maps $$$\hat{u}$$$ for each quantitative map.UP-Net Training Strategy: We designed a loss function with 5 components (Figure 1). (1) $$$L_{imgMSE}$$$: mean-squared error (MSE) loss for images. (2) $$$L_{mapMSE}$$$: MSE loss for maps. (3) $$$L_{imgGAN}$$$ : Wasserstein generative adversarial network (GAN) loss14 for images. (4) $$$L_{physics}=mean(\left \|\hat{m}-Q(\hat{p})\right\|_2^2)$$$ : MRI physics loss where $$$Q$$$ synthesizes multi-echo images from output quantitative maps based on a MRI fat/water/R2* model15,16. (5) $$$L_{unc}=\frac{\left\|\hat{p}-p\right\|_{1}}{\hat{u}}+log(\hat{u})$$$: aleatoric uncertainty loss based on a Laplace distribution17. Regularization weights for each term were chosen based on validation results.
We performed step-by-step training (Figure 1), and added phase offsets to the training images for data augmentation18. For final end-to-end training, batch size=24, learning rate=0.001, epochs=100, and AdamW optimizer19 were used.
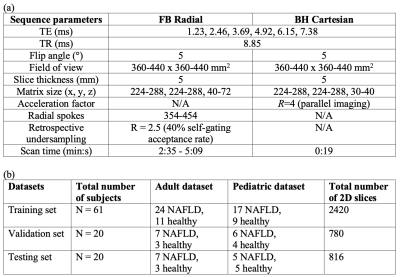
Datasets: In an IRB-approved study, we scanned 101 subjects (Table 1) at 3T (MAGNETOM Skyra or Prisma, Siemens Healthcare, Erlangen, Germany) using (1) a prototype free-breathing multi-echo gradient-echo 3D stack-of-radial sequence (FB Radial)16, and (2) a conventional breath-hold multi-echo gradient-echo 3D Cartesian sequence (BH Cartesian)20. The dataset was split for training:validation:testing datasets in a 3:1:1 ratio.
Since fully-sampled self-gated FB Radial images are not available, after 40% self-gating (2.5-fold undersampling) [3] we performed CS reconstruction by solving21: $$$argmin_x \left\|FSx-y\right\|_2^2+\lambda_1TV_{motion}(x)+\lambda_2\left\|\sum_{echo,state}Wavelet(x_{echo,state})\right\|_1$$$, where $$$F$$$ represents NUFFT, $$$S$$$ denotes beamforming-based coil sensitivity maps22, $$$x$$$ is reconstructed images, $$$y$$$ is acquired k-space data, $$$\lambda_1$$$ and $$$\lambda_2$$$ are regularization parameters. $$$x$$$ was considered as references for UP-Net training and evaluation. Reference quantitative maps were generated by fitting reference images to a multi-peak fat model with a single R2* using graph cut (GC)-based algorithms23,24.
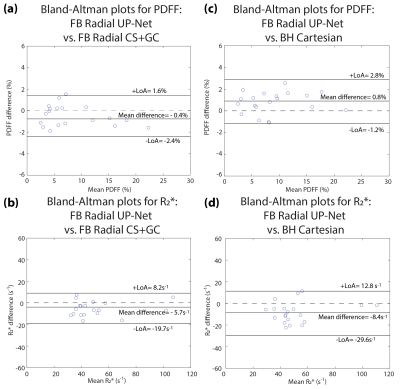
UP-Net Evaluation: (1) Structural similarity index (SSIM) was used to assess the image quality compared to CS. (2) 5-cm2 regions of interest (ROI) were placed in the mid-liver while avoiding large vessels to assess PDFF/R2* accuracy using Bland-Altman analysis. (3) Mean uncertainty scores ($$$\sum_{k\epsilon ROI}\hat{u}$$$) were compared with the mean absolute quantification errors ($$$\sum_{k\epsilon ROI}\left|\hat{p}-p\right|$$$) in mid-liver ROIs.
Results
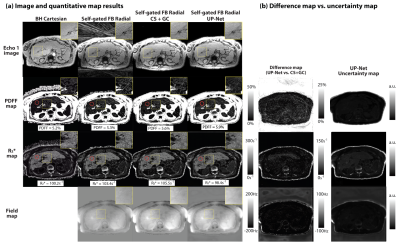
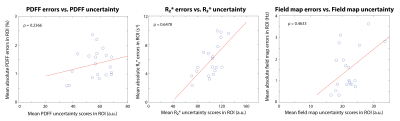
Representative results are shown in Figure 2. Artifact-suppressed images from UP-Net achieved SSIM=0.869$$$\pm$$$0.037 compared with CS reference images. Bland-Altman analysis demonstrated close agreement in liver PDFF and R2* between UP-Net and reference methods (Figure 3). Linear correlation results between quantification errors and UP-Net uncertainty scores for PDFF, R2* and field map were $$$\rho$$$=0.2366, $$$\rho$$$=0.6478* and $$$\rho$$$=0.4633*, respectively (Figure 4; * indicates p<0.01).Reference CS+GC took 15 min/slice on an Intel Xeon E5-2660 CPU. UP-Net required 26 hours for training, and took 81 msec/slice for DL inference on an NVIDIA v100 GPU.
Discussion
UP-Net accurately quantified PDFF and R2* using 40% self-gated images from nominally fully sampled FB Radial data with inference time <100 ms/slice (~4 orders of magnitude reduction vs. CS+GC). Avoiding data oversampling can reduce chances of bulk motion in prolonged scans, and shortened reconstruction time can improve clinical workflows by immediately providing results after scanning.The MRI physics loss term was essential to ensure accuracy for parameter mapping during DL training. The use of uncertainty estimation in DL-based quantitative MRI is still a nascent direction. Compared with recent work11,12, we correlated uncertainty for individual parameters with quantification errors and evaluated the performance in a larger dataset. Uncertainty estimation could potentially assist clinical decisions that rely on accurate quantitative maps. In this work, we found monotonic increase of uncertainty scores vs. quantification errors. Future work can investigate if higher-order functions could better capture the underlying relationship.
There are limitations in this work. First, diagnostic quality of reconstructed image/maps were not assessed by radiologists. Second, the current uncertainty loss term only captures aleatoric (data) uncertainty. Other types of uncertainty (e.g., model uncertainty) can be explored in the future.
Conclusion
We developed a new deep learning network, UP-Net, which achieves rapid and accurate liver PDFF and R2* quantification with uncertainty estimation for free-breathing stack-of-radial MRI.Acknowledgements
The authors thank Dr. Tess Armstrong and MRI technologists at UCLA for data collection, and thank Dr. Xiaodong Zhong at Siemens for technical support. This project was supported by the UCLA Radiological Sciences Exploratory Research Program and the National Institute of Diabetes and Digestive and Kidney Diseases (R01DK124417).References
1. Vernon G, Baranova A, Younossi Z. Systematic review: the epidemiology and natural history of non‐alcoholic fatty liver disease and non‐alcoholic steatohepatitis in adults. Alimentary Pharmacology & Therapeutics 2011;34(3):274-285.
2. Hankins JS, McCarville MB, Loeffler RB, Smeltzer MP, Onciu M, Hoffer FA, Li C-S, Wang WC, Ware RE, Hillenbrand CM. R2* magnetic resonance imaging of the liver in patients with iron overload. Blood, The Journal of the American Society of Hematology 2009;113(20):4853-4855.
3. Zhong X, Armstrong T, Nickel MD, Kannengiesser SA, Pan L, Dale BM, Deshpande V, Kiefer B, Wu HH. Effect of respiratory motion on free‐breathing 3D stack‐of‐radial liver relaxometry and improved quantification accuracy using self‐gating. Magnetic Resonance in Medicine 2020;83(6):1964-1978.
4. Armstrong T, Zhong X, Shih S-F, Felker E, Lu DS, Dale BM, Wu HH. Free-breathing 3D stack-of-radial MRI quantification of liver fat and R2* in adults with fatty liver disease. Magnetic Resonance Imaging 2021 In press.
5. Schneider M, Benkert T, Solomon E, Nickel D, Fenchel M, Kiefer B, Maier A, Chandarana H, Block KT. Free‐breathing fat and R2* quantification in the liver using a stack‐of‐stars multi‐echo acquisition with respiratory‐resolved model‐based reconstruction. Magnetic Resonance in Medicine 2020;84(5):2592-2605.
6. Han Y, Yoo J, Kim HH, Shin HJ, Sung K, Ye JC. Deep learning with domain adaptation for accelerated projection‐reconstruction MR. Magnetic Resonance in Medicine 2018;80(3):1189-1205.
7. Aggarwal HK, Mani MP, Jacob M. MoDL: Model-based deep learning architecture for inverse problems. IEEE Transactions on Medical Imaging 2018;38(2):394-405.
8. Goldfarb JW, Craft J, Cao JJ. Water–fat separation and parameter mapping in cardiac MRI via deep learning with a convolutional neural network. Journal of Magnetic Resonance Imaging 2019;50(2):655-665.
9. Andersson J, Ahlström H, Kullberg J. Separation of water and fat signal in whole‐body gradient echo scans using convolutional neural networks. Magnetic Resonance in Medicine 2019;82(3):1177-1186.
10. Cho J, Park H. Robust water–fat separation for multi‐echo gradient‐recalled echo sequence using convolutional neural network. Magnetic Resonance in Medicine 2019;82(1):476-484.
11. Shih S-F, Kafali SG, Armstrong T, Zhong X, Calkins KL, Wu HH. Deep learning-bassed liver fat and R2* mapping with uncertainty estimation using self-gated free-breathing stack-of-radial MRI. Proc Intl Soc Mag Reson Med 2020.
12. Shih S-F, Kafali SG, Armstrong T, Zhong X, Calkins KL, Wu HH. Deep learning-based parameter mapping with uncertainty estimation for fat quantification using accelerated free-breathing radial MRI. 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI); 2021. IEEE. p 433-437.
13. Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation. International Conference on Medical Image Computing and Computer-Assisted Intervention; 2015. Springer. p 234-241.
14. Hu H, Yokoo T, Hernando D. Multi-site, multi-vendor, and multi-platform reproducibility and accuracy of quantitative proton-density fat fraction (PDFF) at 1.5 and 3 Tesla with a standardized spherical phantom: Preliminary results from a study by the RSNA QIBA PDFF Committee. Proc Intl Soc Mag Reson Med; 2019.
15. Ren J, Dimitrov I, Sherry AD, Malloy CR. Composition of adipose tissue and marrow fat in humans by 1H NMR at 7 Tesla. Journal of Lipid Research 2008;49(9):2055-2062.
16. Armstrong T, Dregely I, Stemmer A, Han F, Natsuaki Y, Sung K, Wu HH. Free‐breathing liver fat quantification using a multiecho 3 D stack‐of‐radial technique. Magnetic Resonance in Medicine 2018;79(1):370-382.
17. Kendall A, Gal Y. What uncertainties do we need in bayesian deep learning for computer vision? arXiv preprint arXiv:170304977 2017.
18. Ong F, Cheng JY, Lustig M. General phase regularized reconstruction using phase cycling. Magnetic Resonance in Medicine 2018;80(1):112-125.
19. Loshchilov I, Hutter F. Decoupled weight decay regularization. arXiv preprint arXiv:171105101 2017.
20. Zhong X, Nickel MD, Kannengiesser SA, Dale BM, Kiefer B, Bashir MR. Liver fat quantification using a multi‐step adaptive fitting approach with multi‐echo GRE imaging. Magnetic Resonance in Medicine 2014;72(5):1353-1365.
21. Feng L, Axel L, Chandarana H, Block KT, Sodickson DK, Otazo R. XD‐GRASP: golden‐angle radial MRI with reconstruction of extra motion‐state dimensions using compressed sensing. Magnetic Resonance in Medicine 2016;75(2):775-788.
22. Mandava S, Keerthivasan MB, Martin DR, Altbach MI, Bilgin A. Radial streak artifact reduction using phased array beamforming. Magnetic Resonance in Medicine 2019;81(6):3915-3923.
23. Hernando D, Kellman P, Haldar J, Liang ZP. Robust water/fat separation in the presence of large field inhomogeneities using a graph cut algorithm. Magnetic Resonance in Medicine 2010;63(1):79-90.
24. Cui C, Wu X, Newell JD, Jacob M. Fat water decomposition using globally optimal surface estimation (GOOSE) algorithm. Magnetic Resonance in Medicine 2015;73(3):1289-1299.
25. Hu J, Shen L, Sun G. Squeeze-and-excitation networks. Proceedings of the IEEE conference on computer vision and pattern recognition; 2018. p 7132-7141.
26. Cole E, Cheng J, Pauly J, Vasanawala S. Analysis of deep complex‐valued convolutional neural networks for MRI reconstruction and phase‐focused applications. Magnetic Resonance in Medicine 2021;86(2):1093-1109.
Figures