Introduction

Diffusion pore imaging¹ (DPI) so far was mostly conducted in artificial phantom systems that excluded extraporal signal contributions. In last year’s ISMRM abstract² we were able to show that by adding filter gradients to the original long-narrow scheme, it is indeed possible to acquire diffusion pore images in the presence of extraporal signals. However, this still implies negligible exchange between the intra- and extraporal space, and the resulting gradient scheme is quite sophisticated. Therefore, an easier solution based on the Gaussian phase approximation is proposed in this study that is applicable for the correction of both extraporal signal contributions and effects originating from exchange between intra- and extraporal space.

Methods

The specialized diffusion encoded sequence used for DPI is depicted in Figure 1a. This approach is called the long-narrow gradient scheme and the refocusing condition for the gradients needs to be fulfilled:
$$\int^{T}_{0}\vec{G}_{\delta_\text{L},\delta_\text{S}}(t)dt=0$$
Considering multiple pores with no extraporal detectable medium, in the limit of $$$\delta_\text{L}\rightarrow\infty,\delta_\text{S}\rightarrow0$$$, the average pore space function (PSF) of the pores illustrated in Figure 1b can be reconstructed from the measured signal $$$S_{\infty,0}(\vec{q})$$$ via a simple inverse Fourier transform:
$$\rho_\text{avg}(\vec{x})=iFT(S_{\infty,0}(\vec{q}))(\vec{x})=\sum^{M}_{n=1}f_n\rho_n(\vec{x}-\vec{x}_\text{CM})$$
where $$$\rho_n(\vec{x}-\vec{x}_{\text{CM}})$$$ is the pore space of the n-th pore shifted to the origin, $$$f_n=V_n/V$$$ is the respective volume fraction within the total intraporal volume $$$V$$$ and $$$\vec{q}=\gamma\vec{G}_\text{L}\delta_\text{L}=\gamma\vec{G}_\text{S}\delta_\text{S}$$$. If also extraporal signals of an NMR-visible medium are allowed and assuming that the extraporal component follows the Gaussian phase approximation³, the signal can be modeled using $$$S_\text{extra}(\vec{q})=S_{0,\text{extra}}e^{-\vec{q}^2c_1}$$$ where $$$c_1$$$ is a constant for radial acquisitions in $$$q$$$-space. The projections in $$$x$$$-space obtained from radial acquisitions can then be written as
$$S(x)=S_0[f_\text{e}e^{-\vec{x}^2c_2}+(1-f_\text{e})iFT(S_{\delta_\text{L},\delta_\text{S}}(\vec{x})]$$
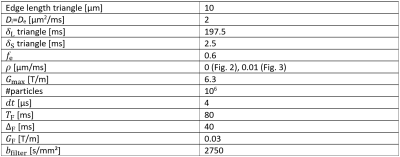
where $$$f_\text{e}=V_\text{e}/V_\text{total}$$$ is the extraporal volume fraction and a constant $$$c_2$$$. If the signal drop of the extraporal component is significantly faster than the intraporal one, in the long-time limit $$$e^{-\vec{x}^2c_2}$$$ becomes broad in $$$x$$$-space and can be fitted by a Gaussian for retrospective removal of the contamination by subtracting it from the actual projection of the PSF. Simulations were carried out using our in-house developed Monte-Carlo simulation tool⁴ implemented in MATLAB. Simulation parameters used for the equilateral triangles can be found in Table 1. Thirty-two gradient directions were simulated in order to be able to reconstruct the two-dimensional pore space images using an inverse Radon transformation.

Results

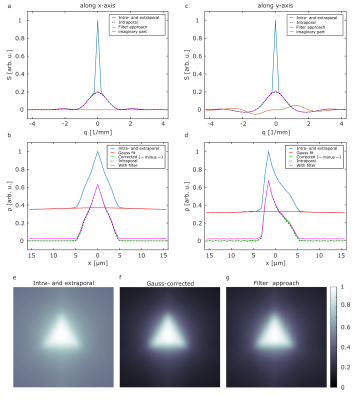
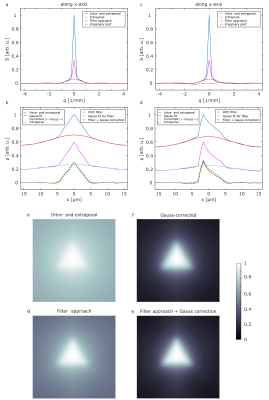
Figure 2 shows the simulated signals (a,c) and corresponding projections of the PSF (b,d) for two representative gradient directions (x-,y-direction). It is obvious that the extraporal signal leads to a deviation for small values that results in a baseline in the reconstructed projections of the PSF and in the pore image without any correction (e). The filter approach (magenta) that we previously proposed is in good agreement with the simulation of only intraporal contributions for both the signal and the reconstructed projection. However, a small remaining baseline is still present. The Gauss-corrected projection of the PSF shows no deviation from the intraporal simulation and yields a slightly higher contrast in the reconstructed image (f) when compared to the filter approach (g). Simulations also considering permeable membranes of the triangles are shown in Figure 3. When comparing the signals in Fig. 3(a,c) to the ones in Figure 2(a,c), it is clearly visible that the deviations from the expected signal are quite severe. Using the filter approach (magenta) the deviation gets smaller; however, a quite significant deviation remains. This deviation carries on to the projections of the PSF (b,d) and the reconstructed images (e,g). When applying the proposed Gauss correction to both the direct measurement and the filter approach, it is indeed possible to obtain the projection of the PSF with almost no deviation from intraporal simulations. This also translates to reconstructed pore images (f,h) that are indistinguishable from the ones presented in Figure 2.

Discussion and Conclusion

Using our proposed correction method, the simulations indicate that it is indeed possible to also apply DPI to pores that are not completely closed, thereby simplifying the acquisition of pore imaging data in the presence of extraporal signals and exchange. For very low packing densities, the extraporal contribution to the signal is rather large. Since the extraporal diffusion is very likely to be Gaussian in that case, it can easily be removed by one of our proposed methods. When considering larger packing densities, the extraporal contributions may become very small; nevertheless, these contributions will be harder to remove since the signal in the extraporal space will also decay much slower and the Gaussian phase approximation may not be valid anymore. Regarding exchange, the applicability will be limited by the necessity to reach the long-time limit within the pores. While general limitations such as the high necessary gradient amplitude are still a concern for the application of DPI for in vivo measurements, cell samples or small animals on preclinical systems represent the natural next step to be investigated using the correction methods presented here. Regarding human in vivo applications, especially local gradient coils might open a perspective due to the high gradient amplitudes they may provide, potentially opening a new window for further insight into pathologies^5,6.

Acknowledgements

No acknowledgement found.