Introduction

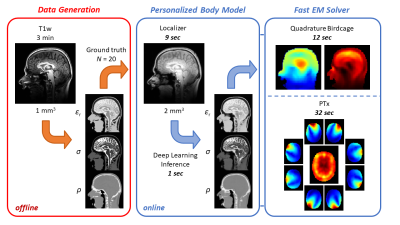
Ultra-high field (UHF) MRI (B₀>7T) shows great promise to yield higher resolution structural and physiological information than available at 3T, particularly in the brain. Parallel RF transmission (PTx) is a key technology for UHF-MRI to address the increased spatial variations in the radiofrequency (RF) field distribution. However, currently it has failed to reach widespread clinical adoption. The main factors include the intersubject variability in local specific absorption rate (SAR), which leads to large safety margins to ensure compliance to regulatory limits^1,2, and time-consuming B₁⁺ calibration procedures required for tailored RF pulse design. Together, these technological challenges limit the clinical impact of PTx and the utilization of UHF-MRI.

In this work, we demonstrate a fast subject-specific method based on deep learning and a fast EM solver for predicting both local SAR and B₁⁺ fields using only a 9 second long localizer scan. A schematic overview of the approach is shown in Figure 1.

Methods

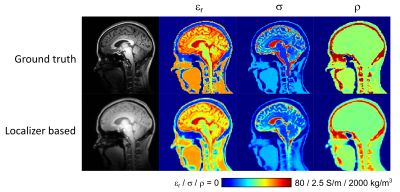
MR protocol: Data was acquired in 20 healthy volunteers (10 male, 10 female, age range 21-66 years) on a Philips Achieva 7T MRI system equipped with a Nova Medical birdcage head coil and integrated 32-channel receive coil array. The imaging protocol consisted of a 3D T₁-weighted MP-RAGE sequence acquired at 1 mm isotropic resolution in 3 min, followed by a fast 3D T₁-weighted localizer acquired at 2 mm isotropic resolution in 9 s.

The 1 mm T₁-weighted data were first used to generate subject-specific dielectric body models with eight tissue classes using our recently developed deep learning segmentation method³. The resulting material parameter maps (i.e. permittivity, conductivity, density) were subsequently downsampled to 2 mm and used as ‘ground truth’ data for training the deep learning network with the localizer as input.

Deep Learning: A 2.5D convolutional neural network was implemented based on the ForkNET topology⁴. The network was designed to have one input and 5 outputs, consisting of the three tissue parameters and additional masks for the background and internal air. The network was implemented using TensorFlow and trained in 100 epochs using a mean squared error loss function. To ensure generalizability, the results were tested in a leave-one-out manner, in which the test subject was excluded from the training data.

EM Solver: The B₁⁺ field and 10 g-averaged SAR distribution (SAR_10g) in the ground truth and localizer-based body models were simulated using a previously developed custom EM solver based on the volume integral equation method⁵. The solver employs a numerical Green’s tensor computed via FDTD and includes a pre-computed coil response library to account for the loading of the RF coil. Incident fields for a quadrature birdcage as well as a generic PTx loop array were simulated using FDTD (XF7.4, Remcom inc., State College, PA) and the solver was implemented in Matlab (2021a, Mathworks inc., Natick, MA) facilitating parallel computing and GPU acceleration through an Nvidia K40 GPU. Channelwise E-fields were combined to construct Q-matrices, averaged over 10 g and processed into a SAR oracle format to facilitate efficient SAR evaluation^6,7.

Results

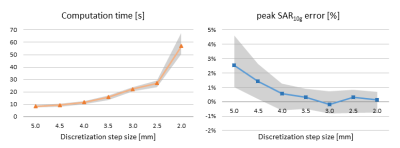
Training of the deep learning network took approximately 160 min and final inference took approximately 1s per subject. A comparison between ground truth and localizer-based dielectric body models is shown in Figure 2.

Figure 3 shows a convergence analysis of the EM solver with respect to discretization step size, evaluated in the birdcage configuration. The peak local SAR error drops below ~1% on average for spatial resolutions of 4.0 mm and higher, which strikes an appropriate balance with an average computation time of 12s. In the eight-channel PTx configuration, the average computation time was 32s, including parallel computing overhead.

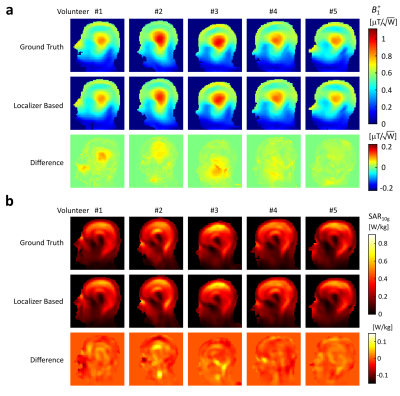
Quadrature birdcage simulations in five of the ground truth and localizer-based body models are shown in Figure 4. Overall, peak SAR_10g values obtained in the network generated body models are within 5% of those obtained in the ground truth body models.

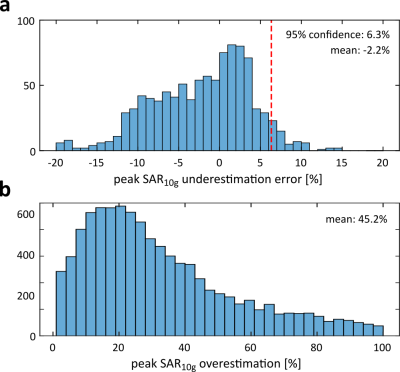
Peak SAR_10g predictions in 1000 random PTx excitations were evaluated against those obtained in the corresponding ground truth body models, summarized in Figure 5. The average peak SAR_10g overestimation in the localizer-based models was 2.2% and an additional 6.3% safety margin would be required to ensure a conservative local SAR estimate in 95% of the cases. This is a considerable improvement compared to the average overestimation of 45.2% that would be obtained by assuming worst-case local SAR values.

Discussion/Conclusion

This work presents a method for local SAR and B₁⁺ prediction using only a short localizer as an input. The total procedure can be executed in less than 30 seconds for the birdcage and less than 45 seconds for the PTx configuration, enabling seamless integration into the MR workflow. As a localizer is acquired at the start of any MR protocol, and the resulting B₁⁺ information can replace time-consuming B₁⁺ calibration procedures, the method does not place a time burden on the MR examination. The SAR predictions can be used to personalize the safety margins, design SAR-optimized RF pulses to safely increase the headroom in allowed sequence parameters.

Acknowledgements

The authors thank Dr. Chloé Najac and Kevin Keene for assistance in data acquisition. This work was supported by the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO) through a VENI fellowship (TTW.16820).