0371
Selective Encoding through Nutation and Fingerprinting (SENF): 1D Experimental Validation on a 47.5 mT Low-Field Scanner
Christopher E Vaughn1,2, N Reid Bolding3, Mark A Griswold4, and William A Grissom1,2
1Department of Biomedical Engineering, Vanderbilt University, Nashville, TN, United States, 2VUIIS, Vanderbilt University, Nashville, TN, United States, 3Physics, Case Western Reserve University, Cleveland, OH, United States, 4Radiology, Case Western Reserve University, Cleveland, OH, United States
1Department of Biomedical Engineering, Vanderbilt University, Nashville, TN, United States, 2VUIIS, Vanderbilt University, Nashville, TN, United States, 3Physics, Case Western Reserve University, Cleveland, OH, United States, 4Radiology, Case Western Reserve University, Cleveland, OH, United States
Synopsis
B0 gradients have several problems including cost, bulkiness, noise, and PNS. We propose to use a method called Selective Encoding through Nutation and Fingerprinting (SENF) which is a RF spatial encoding technique that also encodes quantitative information. In this abstract we validate SENF on a 47.5 mT low-field scanner using a high-flip MR Fingerprinting type sequence with a gradient RF coil to perform a 4-voxel 1D reconstruction that can differentiate between three materials (mineral oil, water, and air).
Introduction
Conventional MRI uses B0 gradients for spatial encoding, which are expensive, bulky, noisy, prone to breakage, and induce PNS. Several spatial encoding methods have been proposed that use RF gradient coils1-4 instead of B0 gradients, but none enable quantitative imaging of T1 and T2 relaxation times. Selective Encoding through Nutation and Fingerprinting (SENF)5, can accomplish RF spatial encoding and quantitative imaging simultaneously using MR Fingerprinting6-like sequences that encode space as additional dimensions. Here SENF is validated on a 47.5 mT low-field scanner in a 1D experiment using a fingerprinting sequence with high-flip angles and TR modulation along with a transmit coil with inhomogeneous B1+ to simultaneously perform spatial encoding and quantitative imaging.Methods
A solenoid transmit coil was analytically designed to produce a linear B1+ field of 1 - 3 gauss over an FOV of 16 cm length and 6 cm diameter when driven with 1.4 A of current. The coil had a 12 cm diameter with variable gaps between winding positions and a variable number of windings per position along its 20 cm length (Figure 1). A saddle coil (diameter 3.5 cm, length 12 cm) sat inside the linear solenoid for receive and was geometrically decoupled from the solenoid by 30 dB. Further decoupling (~40 dB) was achieved using a reed relay T/R switch as a receive gate. Both coils were tuned and matched to 2.075 MHz. A coil holder kept the saddle coil in place and allowed the phantom holder to slide into the center of the FOV of the solenoid. The two coil system was then placed inside a shielded box within the 47.5 mT low-field scanner, to reduce EMI (Figure 2). The pulse sequence had 455 TRs and a total acquisition time of 11.6 seconds. Each TR had a 1500 us hard pulse excitation, a 4 ms (32 point, 8000 Hz BW) acquisition, and a delay that extended the TR. The phase of the hard pulse excitation alternated between 0° and 90° phase each TR. The flip angle and TR length were modulated each TR according to the schedule in Figure 3A. Each excitation peaked at a 18.8 radians flip angle at position 1, allowing for several Myz/Mxz phase cycles across the 4 compartments. The TR was incremented by 8 ms to a maximum of 40 ms. The first half of the sequence had 0 excitation sections following each excitation lobe that increased by ~0.125 seconds to a maximum of 1 second to allow for variable longitudinal recovery. In the experiment 2.5 cm diameter ball phantoms were filled with mineral oil (T1=110 ms, T2=100 ms) or water (T1=2000 ms, T2=1800 ms) and placed into the latter 4 positions of the phantom holder. A signal dictionary is measured by running the sequence with mineral oil and water at each of the 4 locations for a total of 8 data sets with 16 averages. Repetitions that deviated by more than 25% of the mean signal were rejected. The remaining acquisitions for each data set were averaged to form each single dictionary entry, resulting in a total of 8 dictionary entries (4 positions x (mineral oil or water)). Data was then taken for mineral oil phantoms in positions 1 and 3, for water phantoms in positions 1 and 3, and for alternating mineral oil and water phantoms in the 4 positions (Figure 5). For these single data sets any repetition with a deviation greater than 6% from the mean of all acquisitions was discarded, and the remaining were averaged. A regularized least squares fit was performed between each of the data sets and the experimental dictionary. The material at each position (mineral oil, water, or air) was identified at each position by taking the maximum coefficient between mineral oil and water, but the position was set to air if the maximum coefficient was less than 0.35.Results
Figure 1 shows the Biot-savart simulations. The linearity of the solenoid was high (R2 = 0.99757) along the center of the 16 cm FOV, which agrees with the experimentally measured field (R2 = 0.99563) (Figure 1). Figure 5 shows that the three data sets with different phantom configurations were accurately reconstructed. The average coefficient was 0.8895 for mineral oil, 0.6985 for water, and 0.1971 for air.Discussion
The presented experimental results validate SENF for 1D reconstructions on a 47.5 mT low-field scanner. We have shown for the first time that encoding of an NMR signal can be done without using B0 gradients using SENF with high quality results. Future work will improve the encoding power of the sequence for finer resolution across tissue types and space. B1+-Selective excitation pulses7-8 will be implemented using customized RF power amplifiers9 to produce more incoherent signal evolutions across space and tissue types. The linear B1+ field of this optimized coil will allow uniform-width excitation passbands in these pulses, for uniform spatial resolution. Finally, we will implement a parallel transmit system using low cost on-board amplifiers9,10 to validate SENF in 2D.Acknowledgements
Funding source R01 EB030414.References
1. D. I. Hoult. Rotating frame zeugmatography. J Magn Reson, 33(1):183–197, 1979. 2. D. Canet. Radiofrequency field gradient experiments. Prog Nuc Magn Reson Spect, 30:101–135, 1997. 3. J. C. Sharp and S. B. King. MRI using radiofrequency magnetic field phase gradients. Magn Reson Med, 63(1):151–161, 2010. 4. U. Katscher, J. Lisinski, and P. Boernert. RF encoding using a multielement parallel transmit system. Magn Reson Med, 63(6):1463–1470, 2010. 5. C. E. Vaughn, M. A. Griswold, W. A. Grissom. MR Barcoding: Gradient-Free MRI Using B1-Selective Parallel Transmission. ISMRM, 2020 6. D. Ma, V. Gulani, N. Seiberlich, K. Liu, J. L. Sunshine, J. L. Duerk, and M. A. Griswold. Magnetic resonance fingerprinting. Nature, 495:187–192, 2013. 7. C. H. Cunningham and M. L. Wood. Method for improved multiband excitation profiles using the Shinnar-Le Roux transform. Magn Reson Med, 42(3):577–584, Sep 1999. 8. W. A. Grissom, Z. Cao, and M. D. Does. B1+-selective excitation pulse design using the Shinnar-Le Roux algorithm. J Magn Reson, 242:189–196, 2014. 9. R. Bolding, C E Vaughn, C Blades-Thomas, W A Grissom, and M A Griswold. Low-cost Modular RFPA Platform for Gradient-Free Quantitative Imaging. Submitted to ISMRM 2022, London. 10. N. Gudino, J. A. Heilman, M. J. Riffe, O. Heid, M. Vester, and M. A. Griswold. On-coil multiple channel transmit system based on class-D amplification and pre-amplification with current amplitude feedback. Magn Reson Med, 70(1):276—289, 2013.Figures
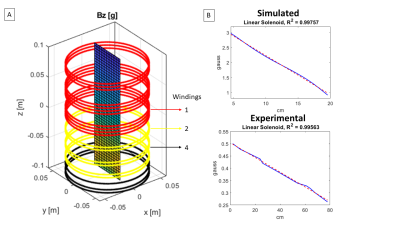
A.) The analytically designed linear solenoid windings
along a 20 cm length to produce a linear 1-3 gauss field within the 16 cm long,
6 cm diameter targeted FOV. B1+ was simulated for a slab
in the center of the full 20 cm length. B.) Left: Simulated 1D B1 profile
across the 16 cm FOV; Right: Experimentally 1D profile.
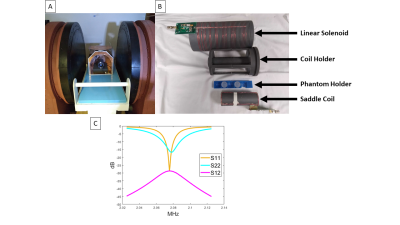
A.) The 47.5 mT scanner and the shielded box with the two coils placed
inside. B.) The linear solenoid, saddle coil, coil holder, and phantom holder
shown separately. C.) The S-parameters for the two coils with the solenoid on
Port 1 and the saddle coil on Port 2, and their decoupling (-30 dB).
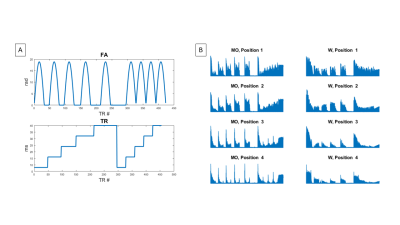
A.)The
flip angle and TR length schedule for each of the 455 TRs of the sequence. B.)
Signal evolutions of the signal dictionary entries.
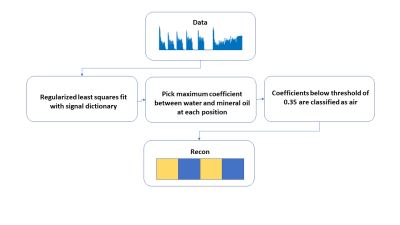
The reconstruction workflow where a regularized least
squares fit is done with the data and the signal dictionary. The maximum
coefficient is chosen between mineral oil and water for each of the 4
positions, and any coefficients below the 0.35 threshold are classified as air.
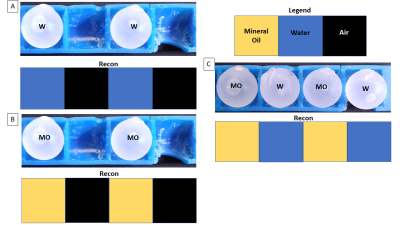
A.) The
water phantoms in position 1 and 3 and their reconstruction. B.) The mineral
oil phantoms in positions 1 and 3 and their reconstruction. C.) The alternating
mineral oil and water phantoms in all positions and their reconstruction.
DOI: https://doi.org/10.58530/2022/0371