0370

Beyond qMRI: Biological tissue properties from single-subject unsupervised deep learning with theoretical signal constraints  
Ilyes Benslimane1, Günther Grabner2, Simon Hametner3, Thomas Jochmann1,4, Robert Zivadinov1,5, and Ferdinand Schweser1,5
1Department of Neurology, Buffalo Neuroimaging Analysis Center, Buffalo, NY, United States, 2Department of Medical Engineering, Carinthia University of Applied Sciences, Klagenfurt, Austria, 3Department of Biomedical Imaging and Image-Guided Therapy, High Field MR Centre, Medical University of Vienna, Austria, 4Department of Computer Science and Automation, Technische Universität Ilmenau, Ilmenau, Germany, 5Center for Biomedical Imaging, Clinical and Translational Science Institute at the University at Buffalo, Buffalo, NY, United States

Synopsis

Most quantitative MRI (qMRI) parameters co-depend on multiple tissue properties, limiting their clinical value. Here, we introduce a biophysically constrained autoencoder network that accepts multiparametric MR data and outputs underlying biological tissue parameters. The method requires no ground truth data, no knowledge of the (generally unknown) biophysical model parameters, and a single subject provides sufficient training data. We validated the method using ex vivo iron and myelin stains.

Introduction

The holy grail of quantitative MRI (qMRI) is the accurate and precise quantification of clinically relevant biological tissue properties. Progress has been made in the fast and reliable acquisition of the classical MRI quantities (T1, T2, R2*, PD, etc.)1 as well as advanced quantities with improved specificity to certain tissue constituents, like MTR (myelin)2 or QSM (iron).3 However, qMRI’s clinical relevance remains limited in part because research has shown that qMRI quantities co-depend on multiple tissue properties (e.g., iron and myelin) and are not specific to any single tissue property. This limitation rendered the interpretation of qMRI findings challenging and diminished clinical impact. Recently, successful efforts have been made to improve qMRI’s specificity through combining multiple qMRI quantities4 but incorporating competing signal sources of iron and myelin with relevant non-linear models remains unachieved. Furthermore, essential physical parameters of the employed signal models are rarely known with sufficient precision and may vary between subjects or be affected by disease.

Here, we introduce a powerful framework for producing tissue property maps with high biological specificity from multiple (unspecific) qMRI metrics. Our method relies on an unconventional application of the autoencoder-type network architecture that enforces known functional relationships between qMRI quantities and tissue properties and can be trained without ground truth data and with just a single scan. Furthermore, it is fully agnostic of signal model parameters. We demonstrate the method in a realistic brain model and in vivo and validate it ex vivo.

Methods

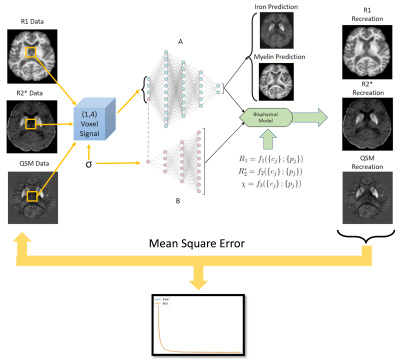
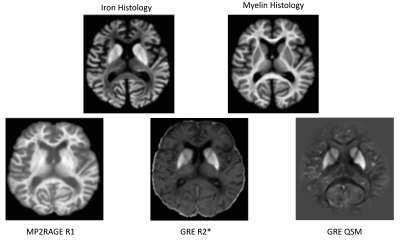
Neural Network Architecture: We propose an autoencoder-type network (Fig. 1) that decomposes a set of measured qMRI quantities{si} (input layer) into two sets of (unknown) parameters (in the autoencoder “bottleneck”): (i) biological tissue parameters {cj} (e.g., myelin and iron concentrations) and (ii) function parameters {pj} that define the functional relationships {cj} → {si} together with function families that are analytically defined in the decoder network part. An additional (a priori) input parameter σ enables {pj}-dependence on tissue type (e.g., WM, GM). Two independent fully-connected networks (A and B in Fig. 1) were used as encoders for the prediction of {cj} and {pj}. The architecture can be trained on single-subject qMRI without ground truth data for {cj} or {pj}, both of which are generally unavailable in vivo.

Ex vivo brain: We performed R1, R2*, and susceptibility mapping (QSM) of a cadaver head at 7T (Fig. 2). The brain was stained for iron and myelin (Fig. 2) and qMRI maps were manually co-registered to the stains.

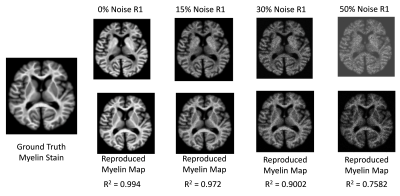
Brain model creation: To create a realistic digital brain model, we forward-simulated R1, R2*, and χ from the iron and myelin stains using linear models (Fig. 2) and added varying degrees of Gaussian noise (Fig. 3).

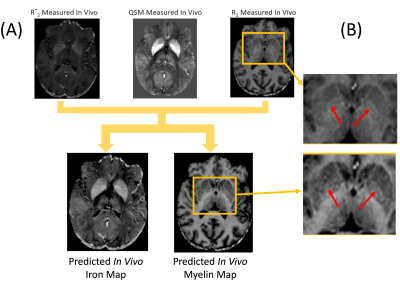
In vivo brain: We scanned a volunteer using a multi-echo GRE based qMRI protocol at 3T (matrix=328x256x70, 0.7x0.9x1.8 mm3, TE1/DTE=4ms/2.5ms; flip/nTE/TR Seq1: 14°/10/30ms, Seq2: 14°/6/30ms, Seq3: 14°/4/15ms; Seq2: MTC flip/offset 350°; 2kHz) and reconstructed R1, R2*, PD, MTS 5,6, and QSM7.

Evaluation and validation: We considered a three-compartment tissue model with iron (cFe) and myelin (cMy) in a tissue matrix using first/second-order function families depending on quantity. First, we trained the network (ADAM8, implemented with TensorFlow 2.2.0; NVIDIA GeForce RTX 2080 Ti) using the simulated brain model maps for each noise level. To test the method in real-world data, we repeated the training with the measured ex vivo and in vivo qMRI maps.

Results

Training completed after 2 minutes (2000 epochs; stable training loss). Noise-free simulations resulted in a perfect prediction of concentration maps (Fig. 3), and predictions were robust for moderate noise levels (Fig. 3). Quadratic signal families resulted in a high correspondence with the ground truth (Fig. 4). In vivo results were similar to those obtained ex vivo, showing expected contrast in the WM and deep GM (Fig. 5).

Discussion

The lack of biological specificity represents a barrier toward a clinical translation of qMRI. The proposed method leverages the co-dependence of qMRI to infer on the truly relevant biological tissue properties, thereby considering qMRI not as the goal but only as an intermediate step toward true tissue quantification.

Our results demonstrate the resolution of co-dependences on iron and myelin in current qMRI techniques. Computed iron and myelin maps qualitatively resembled the contrast on stains. Deviations, relative to the iron stain, may be related to the simplistic signal models used here as well as the qualitative nature of the TBB stain.

Different from previous attempts, the proposed method yields critical biophysical constants, such as the relaxivity of tissue iron, as part of the training process. With the ability to train the network on a single subject, pathological alterations in these constants can be directly studied and do not have to be imputed a priori. In this proof-of-concept work, we used simple function families for the signal models and only a small number of qMRI methods. However, arbitrarily complex signal models may be used and the method will benefit from recent advances in fast qMRI acquisition schemes.

Conclusion

The proposed framework leverages limitations of qMRI metrics to quantify biological tissue properties based on signal function families derived from biophysical considerations.

Acknowledgements

Research reported in this publication was partially supported by the National Institute Of Neurological Disorders And Stroke of the National Institutes of Health under Award Number R01NS114227, the National Center for Advancing Translational Sciences of the National Institutes of Health under Award Number UL1TR001412, and by an equipment grant from Canon Medical Systems Corporation and Canon Medical Research USA, Inc. The content is solely the responsibility of the authors and does not necessarily represent the official views of the funding agencies. Furthermore, the research was supported by the Free State of Thuringia within the ThiMEDOP project (2018 IZN 0004) with funds of the European Union (EFRE), and the Free State of Thuringia within the thurAI project (2021 FGI 0008).

References

[1] Chen Y, Chen MH, Baluyot KR, Potts TM, Jimenez J, Lin W; UNC/UMN Baby Connectome Project Consortium. "MR fingerprinting enables quantitative measures of brain tissue relaxation times and myelin water fraction in the first five years of life." Neuroimage. 186:782-793. 2019 Feb 1. doi: 10.1016/j.neuroimage.2018.11.038.

[2] Wolff SD, Balaban RS. "Magnetization transfer contrast (MTC) and tissue water proton relaxation in vivo." Magn Reson Med. 10(1):135-44. 1989 Apr. doi: 10.1002/mrm.1910100113.

[3] Langkammer C., Schweser F., Kreb N. et al. "Quantitative susceptibility mapping (QSM) as a means to measure brain iron? A post mortem validation study" NeuroImage, Volume 62, Issue 3, 2012, Pages 1593-1599, 2012.05.049. ISSN 1053-8119, https://doi.org/10.1016/j.neuroimage.

[4] Warntjes, M., Engström, M., Tisell, A., & Lundberg, P. "Modeling the presence of myelin and edema in the brain based on multi-parametric quantitative MRI". Frontiers in Neurology, 7. 2016. https://doi.org/10.3389/fneur.2016.00016.

[5] Weiskopf N and G Helms "Multi-parameter mapping of the human brain at 1mm resolution in less than 20 minutes". In: Proceedings of ISMRM 16, Toronto, Canada. 2241. 2008

[6] Weiskopf N, Suckling J, Williams G, Correia MM, Inkster B, Tait R, Ooi C, Bullmore ET, Lutti A. "Quantitative multi-parameter mapping of R1, PD*, MT, and R2* at 3T: a multi-center validation." Frontiers in Neuroscience 7:95. 2013

[7] Schweser, F., Sommer, K., Deistung, A., & Reichenbach, J. R. "Quantitative susceptibility mapping for investigating subtle susceptibility variations in the human brain." NeuroImage, 62(3), 2083–2100. 2012. https://doi.org/10.1016/j.neuroimage.2012.05.067.

[8] D. P. Kingma and J. Ba, "Adam: A Method for Stochastic Optimization", Dec. 2014.

[9] Marques JP, Kober T, Krueger G, van der Zwaag W, Van de Moortele PF, Gruetter R. "MP2RAGE, a self bias-field corrected sequence for improved segmentation and T1-mapping at high field." Neuroimage. 49(2):1271-81. 2010 Jan 15. doi: 10.1016/j.neuroimage.2009.10.002.

[10] S. Hametner, I. Wimmer, L. Haider, W. Brück, H. Lassmann, "Iron and oxidative damage in the multiple sclerosis brain", Journal of the Neurological Sciences, Volume 333, Supplement 1, Pages e386-e387, 2013. ISSN 0022-510X, https://doi.org/10.1016/j.jns.2013.07.1403.

Figures

Fig. 1: Proposed architecture. Sub-network A (main inversion network) takes a voxel’s parametric data (here: R1, R2*, QSM) and the a priori defined tissue type index (σ). The σ value is also the sole input in network B (model parameter network). The network bottleneck outputs biological properties {cj} (from A) as well as model parameters {pj} (from B). The forward simulation is performed in an analytical biophysical model layer. The difference between input and output is used as training loss.

Fig. 2: A cadaver head (room-temperature) imaged at 7T using the MP2RAGE sequence9 for T1 mapping and a multi-echo gradient echo sequence for R2* mapping and QSM (bottom row). Following MRI, the brain was fixed for 3 days at room temperature and cut into slices, which were stained with DAB-enhanced Turnbull blue (TBB; top left) for iron and LFB-PAS for myelin (top right).10

Fig. 3: A realistic multiparametric simulation experiment based on ex vivo data. Digital qMRI model were simulated from stains and corrupted with Gaussian noise (top row shows resulting R1 maps). The network was able to predict the underlying myelin map (bottom row) even for high noise levels.

Fig. 4: Application of the method to real-world measured ex vivo qMRI data at 7T. Applied to measured R1, R2* and QSM (left), the method predicted iron and myelin maps (middle). Insets at the bottom compare R1 contrast (affected by both iron and myelin) with predicted myelin and the ground truth myelin stain, demonstrating accurate removal of iron signals in the deep gray matter. Linear model families were insufficient for properly modeling the co-dependencies of the qMRI quantitites.

Fig. 5: Application of the method to measured in vivo volunteer qMRI data at 3T. (A) R1, R2* and QSM maps were used as inputs for the network which predicted iron and myelin maps. (B) The iron-induced hyperintensity on the R1 map in the putamen and globus pallidus are properly reduced on the myelin map, resulting in the expected deep gray matter contrast similar to the stains in Fig. 4.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)
0370
DOI: https://doi.org/10.58530/2022/0370